KMP 模式匹配浅谈
前言
匹配:定义详见:字符串匹配 - OI Wiki
参考资料:
- 《算法竞赛进阶指南》0x15字符串:KMP 模式匹配
KMP 算法
KMP 分为两步
第一步:对模式串自我匹配
设模式串为 \(B\),\(B_{i\sim j}\) 为 \(B\) 中开头位置为 \(i\),结尾位置为 \(j\) 的字串。
考虑求出一个数组 \(nxt\),其中 \(nxt_i\) 为 \(max\{j\}\quad(j\le i,B_{1\sim j}=B_{i-j+1\sim i})\)。换言之,即为 \(B_{1\sim i}\) 中能够匹配的前缀 \(B_{1\sim j}\) 和后缀 \(B_{i-j+1\sim i}\) 中最大的 \(j\)。特别的,若 \(j\) 不存在,则 \(nxt_i=0\)。
下面来说 \(nxt\) 如何求:明显,\(nxt_1=0\)。
考虑通过 \(nxt_{1\sim i-1}\) 求出 \(nxt_i\)。对于能够使 \(B_{1\sim j}=B_{i-j+1\sim i}\) 的 \(j\),我们称它为 \(nxt_i\) 的“待选项”。
定理:若 \(j_0\) 为 \(nxt_i\) 的“待选项”,则小于 \(j_0\) 的下一个最大“待选项”为 \(nxt_{j_0}\)
证明:先证明,\(nxt_{j_0}\) 是 \(nxt_i\) 的“待选项”:
由于 \(j_0\) 为 \(nxt_i\) 的待选项,则 \(B_{1\sim j_0}=B_{i-j_0+1\sim i}\)(相同颜色为相等的字符串)。

又因为 \(nxt_{j_0}\) 是 \(j_0\) 的”待选项“,则 \(B_{1\sim nxt_{j_0}}=B_{j_0-nxt_{j_0}+1\sim j_0}\)

所以 \(B_{1\sim nxt_{j_0}}=B_{j_0-nxt_{j_0}+1\sim j_0}=B_{i-j_0+1\sim i-j_0+nxt_{j_0}}=B_{i-nxt_{j_0}+1\sim i}\)(过于抽象,可以看图)

因此 \(nxt_{j_0}\) 是 \(nxt_i\) 的“待选项”。
再证明,在 \(nxt_{j_0}+1\sim j_0-1\) 之间没有 \(nxt_i\) 的“待选项”:
考虑反证法,不妨假设结论成立,设在 \(nxt_{j_0}+1\sim j_0-1\) 之间 \(nxt_i\) 的“待选项”为 \(j_1\),则 \(nxt_{1\sim j_1}=nxt_{i-j_1+1\sim i}\),又因为 \(nxt_{1\sim j_0}=nxt_{i-j_0+1\sim i}\),则 \(nxt_{1\sim j_1}=nxt_{j_0-j_1+1\sim j_1}\),如图(因为 \(nxt_{j_0}<j_1<j_0\),所以 \(j_0\) 在 \(nxt_{j_0},j_0\) 两者之间):
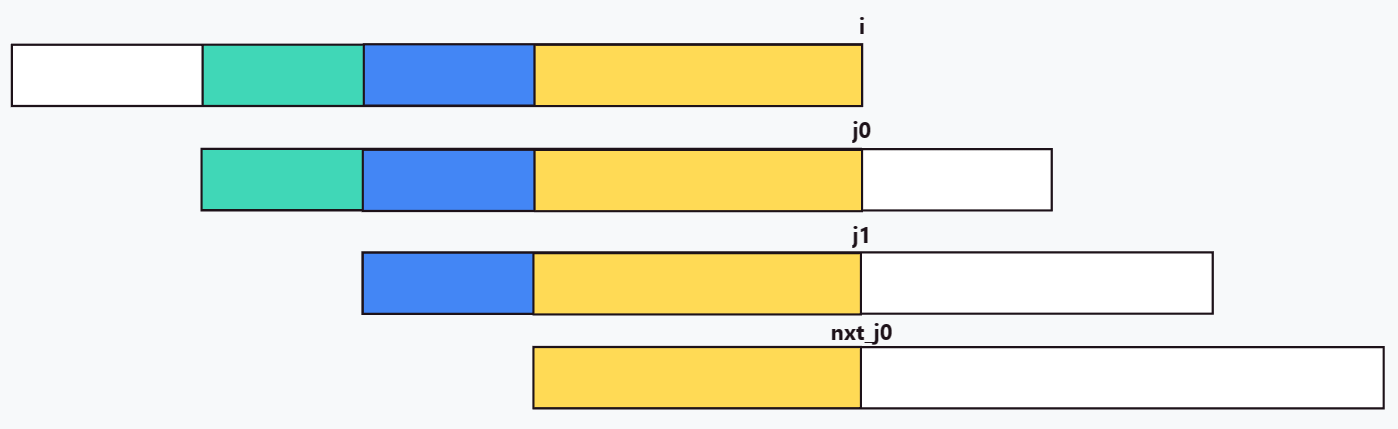
由于 \(nxt_{1\sim j_1}=nxt_{j_0-j_1+1\sim j_1}\),发现 \(j_1\) 为 \(nxt_{j_0}\) 的“待选项”且 \(j_1>nxt_{j_0}\),和 \(nxt_{j_0}\) 的最大性矛盾,原命题得证。
于是根据定理,若 \(j\) 为 \(nxt_i\) 的“待选项”,则 \(nxt_j,nxt_{nxt_j},\cdots\) 等都是 \(nxt_i\) 的“待选项”。
则在求 \(nxt_i\) 时,如果 \(j\) 是 \(nxt_i\) 的“待选项”,则 \(j-1\) 一定是 \(nxt_{i-1}\) 的“待选项”(因为 \(B_{1\sim j}=B_{i-j+1\sim i}\) 的前提条件是 \(B_{1\sim j-1}=B_{i-j+1\sim i-1}\) ),因此只要把 \(nxt_{i-1}+1,nxt_{nxt_{i-1}}+1,\cdots\) 作为 \(j\) 的选项即可,当发现一个 \(B_{nxt_{\cdots}+1}=B_i\) 时,则说明找到了 \(j\) 的值,为 \(nxt_{\cdots}+1\),代码如下(W 为 while,m 为 \(B\) 的长度):
nxt[1] = 0; for (i = 2, j = 0; i <= m; ++ i) {W (j > 0 && B[i] != B[j + 1]) j = nxt[j]; if (B[i] == B[j + 1]) ++ j; nxt[i] = j;}
第二步:将待匹配串和模式串进行匹配
求出了 \(nxt_i\) 后,考虑在求一个数组 \(f_i=max\{j\}\quad(j\le i,B_{i-j+1\sim i}=A_{1\sim j})\),意义和 \(nxt_i\) 相近,含义和求法不再赘述,代码如下:
for (i = 1, j = 0; i <= n; ++ i) {W (j > 0 && (j == m || A[i] != B[j + 1])) j = nxt[j]; if (A[i] == B[j + 1]) ++ j; f[i] = j;}
不难发现,在 \(f_i=m\) 时,则说明找到了一个匹配的子串。
接下来讨论 KMP 的时间复杂度,发现在一个 while 循环结束后,j 被改变的次数不超过 while 循环前后 j 值之差(因为一次 j=nxt[j] 后 j 的值必定减小)。由于 j 值始终非负,所以 j 的减少量不会超过 j 的增加量,于是 j 被改变的次数不超过 \(2(n+m)\),所以 KMP 算法总时间复杂度为 \(\mathcal{O}(n+m)\)
例题
板题:P3375 【模板】KMP字符串匹配
链接:P3375 【模板】KMP字符串匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
solution
进行 KMP 即可,题目中的 border 数组即为 \(nxt\) 数组。
code
CI N = 1e6; string A, B; int n, m, nxt[N + 5];
int main () {
RI i, j; cin >> A >> B; n = A.length (); m = B.length (); A = " " + A; B = " " + B;
nxt[1] = 0; for (i = 2, j = 0; i <= m; ++ i) {W (j > 0 && B[i] != B[j + 1]) j = nxt[j]; if (B[i] == B[j + 1]) ++ j; nxt[i] = j;}
for (i = 1, j = 0; i <= n; ++ i) {W (j > 0 && (j == m || A[i] != B[j + 1])) j = nxt[j]; if (A[i] == B[j + 1]) ++ j; if (j == m) printf ("%d\n", i - m + 1);}
for (i = 1; i <= m; ++ i) printf ("%d ", nxt[i]); printf ("\n");
return 0;
}
AcWing 141.周期
\(\Huge{\text{待填坑}}\)


