学习笔记：分层图（坑）

分层图，（就是分层的图），是用来解决一类带条件的最短路的。我们带着例题来讲。

例题：P4568 [JLOI2011]飞行路线

solution

首先我们将这张图建 \(k+1\) 层，第 \(i\) 层表示用了 \(i-1\) 次免费后的状态。然后我们将相邻两层之间的免费方案连边，连从第 \(i\) 层到第 \(i+1\) 层的有向边，边权为 0，这样每往下走一层就说明使用了一次免费方案。最后我们将所有终点从上到下连起来，跑一边最短路即可，图片如下：

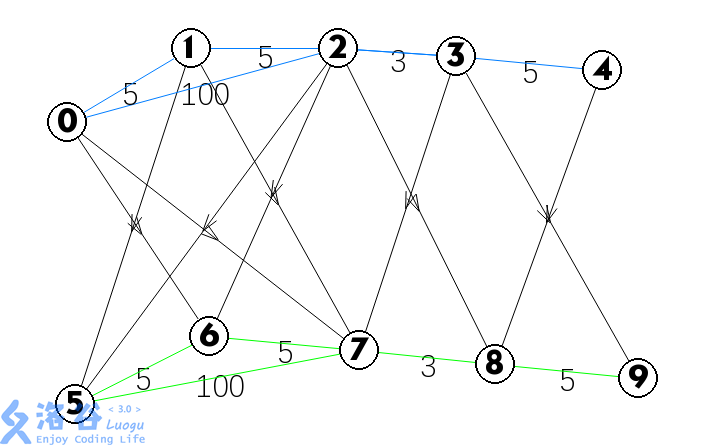
code

#include <bits/stdc++.h>
#define Tp template<typename Ty>
#define Ts template<typename Ty,typename... Ar>
#define I inline
#define ll long long
#define Con const
#define CI Con int
#define RI register int
#define W while
#define gc getchar
#define D isdigit(c=gc())
#define pc(c) putchar((c))
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
#define Gmax(x,y) (x<(y)&&(x=(y)))
#define Gmin(x,y) (x>(y)&&(x=(y)))
#define ms(a,x) memset((a),(x),sizeof(a))
using namespace std;
namespace FastIO
{
	CI FS = 1e5; int Top = 0; char S[FS];
	I void readc (char& c) {W (isspace (c = gc ()));}
	Tp I void read (Ty& x) {char c; int f = 1; x = 0; W (! D) f = c ^ '-' ? 1 : -1; W (x = (x * 10) + (c ^ 48), D); x *= f;}
	Ts I void read (Ty& x, Ar&... y) {read (x); read (y...);}
	Tp I void write (Ty x) {x < 0 && (pc ('-'), x = -x, 0); W (S[++ Top] = x % 10 + '0', x /= 10); W (Top) pc (S[Top --]);}
	Tp I void writeln (Ty x) {write (x); pc ('\n');}
} using namespace FastIO;
#define pii pair<int,int>
#define fi first
#define se second
#define mk make_pair
CI N = 1e6, M = 6e6; int n, m, k, s, t;
int nxt[M + 5], to[M + 5], w[M + 5], head[N + 5], dis[N + 5], cnt = 0; bool vis[N + 5];
void add (int u, int v, int ww) {++ cnt; to[cnt] = v; w[cnt] = ww; nxt[cnt] = head[u]; head[u] = cnt;}
void dij () {
	RI i, j; ms (dis, 0x3f); vis[s] = 1;
	priority_queue <pii, vector <pii>, greater <pii>> q;
	q.push (mk (0, s)); dis[s] = 0;
	W (! q.empty ()) {
		pii p = q.top (); q.pop ();
		int v = p.se; vis[v] = 1;
		for (i = head[v]; i; i = nxt[i]) {
			if (dis[v] + w[i] < dis[to[i]]) {
				dis[to[i]] = dis[v] + w[i];
				if (! vis[to[i]]) q.push (mk (dis[to[i]], to[i]));
			}
		}
	}
}
int main () {
	RI i, j; read (n, m, k, s, t);
	for (i = 1; i <= m; ++ i) {
		int a, b, c; read (a, b, c); add (a, b, c); add (b, a, c);
		for (j = 1; j <= k; ++ j) {
			add (a + (j - 1) * n, b + j * n, 0);
			add (b + (j - 1) * n, a + j * n, 0);
			add (a + j * n, b + j * n, c);
			add (b + j * n, a + j * n, c);
		}
	}
	for (i = 1; i <= k; ++ i) add (t + (i - 1) * n, t + i * n, 0);
	dij ();
	printf ("%d\n", dis[t + k * n]);
	return 0;
}

应用：P5663 [CSP-J2019] 加工零件

solution

code

\(\Huge{坑}\)