网络流
传奇水题板块，我有一万道紫黑都是做网络流，常年做网络流的人都目光呆滞极度自卑智商逐年下降最后完全成为傻子后面忘了。
算法难度-1分，思维难度比较高，至少在2024.6.12还没法靠自己做出来题。
6.14：这个东西当作dp做可能会比较好想，连边操作就是在跑大概的转移方程，网络流就是自动从转移方程里找最优状态。
11.7：水水，水水水。我要做一亿道网络流。
最大流
好像是最大流经典例题，每个单位的人不能坐一张桌子，所以任意一个单位连到桌子的容量为1，意思是只能做一个这样的人，超原给每个单位连 \(r_i\) 容量的边，每个桌子给超汇连 \(c_i\) 的边。跑最大流。
有解是要每个人都落座，看看最大流是不是总人数。
是了暴力扫就行。
这种问题有一个套路，如果你只会最大流而想解决最小值问题，可以用蜥蜴总数减掉能逃离的蜥蜴最大总数。总-最大反答案=最小答案。
也就是说最大流跑出来的就是能跑掉的蜥蜴数。
所以从超原往每个有蜥蜴的柱子连1边，一般从超原连出来的就是最基本的量。
能跳到边缘的点就是出口，只要柱子还在就能一直跳蜥蜴，所以给这些点跟超汇连容量无穷的边。
然后看怎么跑跳柱子减高度的过程。使用拆点：把每个柱子拆成一个入点和一个出点，入点和出点连柱子高度的容量，这样每个蜥蜴上了柱子就一定会占用一个高度容量，也就相当于柱子变矮了。要跳柱子就要从一个柱子出点走到另一个柱子的入点，也是可以无限跳的，连无穷边。
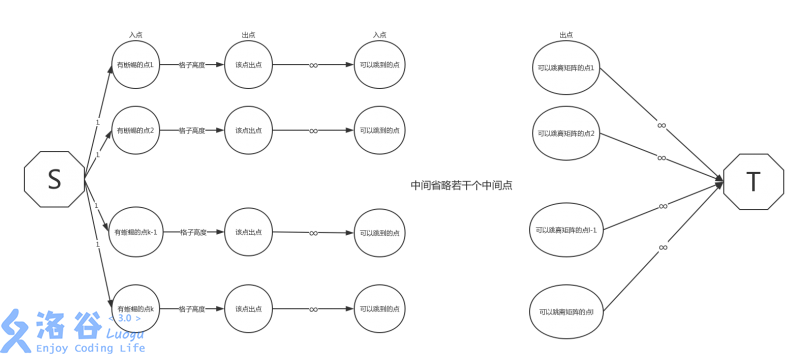
这个是网络流+二分答案。
显然连接武器和能打到的机器人，因为随便打所以容量无穷，机器人连到超汇容量为血量。
然后看为什么要二分答案。
在时间 \(t\) 时每个炮台能一共打出 \(b_i*t\) 的伤害，这些伤害要分布到机器人的血量上，如果现在拿这个数做容量从超原往炮台连边跑最大流，最后跑出来的最大流就是这段时间内炮台能打出来的最大伤害总和。
看一下这个总和大于等于总血量就行了。然后二分答案时间。
二分时间是这类问题的一种常用套路。
用蜥蜴那题的做题思路，看一下最大反答案即最多能空多少个格子。
这种格子问题有一种方法就是 \(x\) 向 \(y\) 即坐标间连边，优势在于：每个兵会同时对 \(l\) 与 \(c\) 产生影响，如果用兵点向lc分别连边（我最早的思路），那么dinic是无法保证最大流会同时流向两个点，模型就错了。
如果是 \(x->y\) 连1边那么每个兵连向x连1边后会继续跑y，跑完就是一个坐标点。
既然空点要最大，按照题意相当于每一行和列都最多空出来一个数，把容量取反跑最大流即可。
还有法2。
可以发现答案再大大不过 \(\sum C_i+\sum L_i\)。答案能不等于这个的原因在于：这种情况下我们认为每个兵只对 \(L,C\) 中的一个产生贡献，但很明显有一些兵可以同时对 \(L,C\) 产生贡献，我们记这个兵数为 \(val\)，那么有 \(ans=\sum C_i+\sum L_i-val\)。
我们发现其实这个 \(val\) 好求的不止一点，把每个超原容量为 \(L_i\) 的 \(x\) 连1边向 \(y\)，\(y\) 以 \(C_i\) 连超汇，那跑出来的最大流不就是两个都贡献的兵吗...
这个题挺恶心。
按照套路尝试去二分答案撤离时间，由于一个门每个时间只能走一个人，可以考虑把每个门按时间拆成小点向超汇连1边。
然后一群人因为有可能会堆在一个门上，所以距离一个点最短的门可能不是这个人的最优出口，我们预处理出每个门点 \(i\) 到某个人点 \(j\) 的距离 \(dis_{i,j}\)，显然这个人想走这个门撤离至少要在 \(tim\ge dis_{i,j}\) 往后。
考虑怎么等，原本想的是直接把人点向这个门于 \(dis\) 后的所有时间门点连边，这个想法太naive。题解做法：每个时间的门向下一个时间的这个门连无穷边，这样只用 \(anstime\) 条边就可以处理所有想走这个门撤离的人的“等待”问题。
然后把每个人往他能到的门上连最短距边，有了刚才的处理我们只需要连一条到时间门的边就可以了。
在每次二分时间得到的图上跑最大流，看看能不能全跑出去。
impossible的情况肯定是有人没门出，最开始就能预处理出来。
细节太多了差评。
这个题空间得往大开否则你就会被各种奇怪溢出导致的诡异错误折磨致死(比如预处理完导致全局都应该不动的超原编号变成15)。
按照套路用二分时间的图跑人数最大流。
现在又会个套路即关于时间的处理：时间可以拿来影响容量（星际战争），也可以拿来按时间拆点影响图的结构（紧急疏散和这道题）。
每个太空站可以塞无限多个人，我们按时间拆好点让每个当前时间的太空站向下个时间的太空站连无穷边，超原连时间0的地球站，时间ans的月球站连超汇。
这样的好处就在于：飞船的运动就非常好处理了，飞船会在每个时间的每个站向下个时间的下个站转移人，我们给他俩连容量边，又因为飞船在任何一个时间的位置都可算，图就可以建出来了。
放一个tj区特别清楚的图。
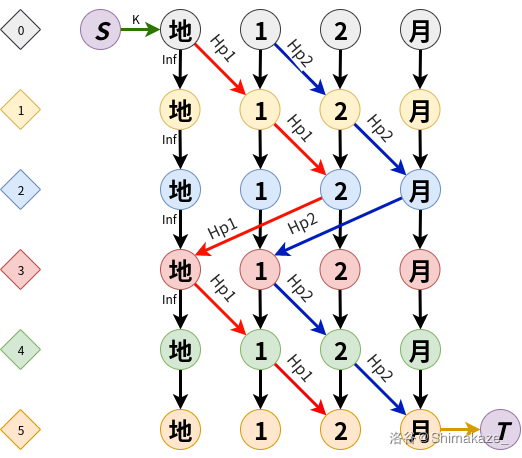
弱智题。
这种双要素的网络流有固定套路：超原连要素1，要素1连元素，元素连要素2。自己随便拆点限流就行了。
但是不要超原->要素1->要素2这么连，要不然你也不知道要素1对应的元素到底能不能到要素2。
不好想的一道题，本来人就菜，题一难直接脑袋空空查看题解。
是这么分析的：
因为每个格子会影响到相邻的格子，所以可以给棋盘黑白染色（听都没听过的处理方法啊喂！）
我们设若干次操作后全部格子变成同一个值 \(v\)，设最早黑白格子的权值和为 \(val_1,val_0\)，格子个数为 \(num_1,num_0\)。那么应该有：
翻译成人话就是黑白格子权值增量相等。
我们可以直接通过网络流方法验证是否成立，怎么验证之后说。
但是 \(num_0==num_1\) 时就不能这么验证了，得慢慢二分答案，答案上界很大，r甚至得到1e18。
这个建图也挺牛逼的，二分答案最终格子的权值 \(v\)，既然已经完成了黑白染色，那么可以从黑格往相邻白格连无穷边，然后超原给黑格连 \(v-a_{loc}\) 边，白格给超汇连 \(v-a_{loc}\) 边，也就是容量即当前权值到目标权值的操作次数，连起来就可以处理黑白格同时加权的操作。我们算黑格的容量和 \(sum\)，跑一个最大流 \(V\)，如果 \(V==sum\) 说明不仅黑白格总权值增量相同，而且都达到了目标权值。
这这这思维太跳脱了，感觉还得练好多题才能想到...
思路想对了，二分答案，女的往超汇连 \(ans\) 边，看看最大流是不是 \(n*ans\) 即可。
然后每个男女从自己都开一个不喜欢点，容量 \(k\)。喜欢了直接人点连 \(1\) 边，不喜欢了就不喜欢点连 \(1\) 边。
但是超原往男点连的也是 \(ans\) 边而不是 \(inf\) 边，这个我想错了，我觉得要贪心给答案所以给的inf，想了一下因为可能出现一些inf海王男点给嗯往女点跑流结果把答案跑大了。
最小割
UPD：2024.6.22:唐氏课件把最小割放费用流后头，网上自学完了才发现后面有。
有一个最小割最大流定理，因为最大流在增广时会收到minf边的限制，那么这些minf边合起来就是最小的割。感性理解一下就行。
进而最小割容量就是最大流。
为了“割”的有效即选择关系更明确，经验来看，最小割题目一般不给图分层。
最小割可以用于这种“选了A就不能选B”题目的处理。
如果不考虑同时选课给出的贡献，那么建图就比较容易了（不应该直接取max吗），S给人点连文科边，人点再给T连理科边，按照意义来看，我们给这图跑一个最小割就是不选科目的最小损失即最优反答案，不按照意义看就直接跑最大流。
然后考虑怎么处理同时选课。
手玩可以发现，如果你要用最小割做这个题，那么被切除的边提供的combo也应该被切除，或者说，在这个割内，再按照最大流的原理，combo分的容量边很可能是与S(T)相连的。
事实就是这样，我们从S像一个辅助点连文combo边，再从辅助点往两个相邻的人点连无穷边，对称一个辅助点处理理科。这样就会导致：如果我们要割掉这两个人点的文理边导致图不连通，那么他们的combo边也必须被割掉（肯定不断inf），要不然这两条边没有断掉的意义。
放一张tj图。
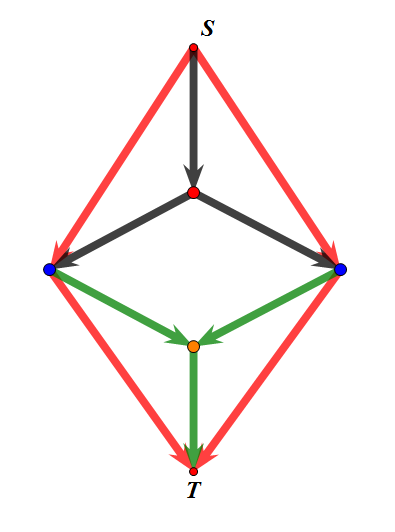
难搞。
又 \(a_i\in\{0,1\}\)，相当于成了贡献前的条件。
对于每个 \(b_{j,i}\)，仅当 \(a_i=a_j=1\) 时才能产生贡献。
但同时的，一旦 \(a_i=1\) 将产生 \(c_i\) 的负贡献。现在要让正负贡献之和最大。
我们把 \(b_{j,i}\) 求和，超原往 \(b_{j,i}\) 连贡献边，\(c_i\) 往超汇连边，对应 \(b\) 往对应 \(c\) 连无穷边。
这样有一个什么效果：跑最小割时要么割断 \(b_{j,i}\)，要么割 \(c\)，我们拿刚才求的和对这个最小割作差，相当于要么保留原有 \(b_{j,i}\) 的贡献但是得给我扣掉 \(c\)，要么不扣 \(c\) 但是减掉你 \(b_{j,i}\) 的贡献。
原本用的happiness的方法，然后10pts。
先说我错的思路，想的是人往超汇连 \(a_i\) 边，超原往 \(ij\) 辅点连 \(3E_{i,j}(j>i)\) 边，汇总 \(2*E\) 然后减去最小割。
如果只有一个人不选那么是正确的，问题是：如果 \(i,j\) 两个人都不选那么这个模型会额外扣掉一个 \(E_{i,j}\)。
然后看人说是最小割有一个原连小点，小点连汇，小点互联的常用套路。
看一下两个人选取贡献吧：
- 两个都选，最后要减掉他们的 \(A_i\)，贡献为向其他选取经理的combo贡献和，这俩人的combo贡献也得加上。
- 选一个，剪掉一个 \(A_i\)，加上选的人和其他人的combo和，减掉另一个人和其他人（包括这个选的人）的combo和。
- 都不选，不用减 \(A_i\)，但是他俩向其他所有选取人的combo和得减，但他俩之间的combo不用减。
如果不考虑不选造成的负贡献，那就超原往人点连其引导的和贡献边，人点往超汇连 \(A_i\) 边，要么掏 \(A_i\) 钱要么丢正贡献。
但是现在不掏 \(A_i\) 的钱还会导致他到其他所有点都产生 \(E_{i,j}\) 的负贡献，而且一扣扣俩，\((i,j),(j,i)\) 各一次，所以从 \(i\) 向所有 \(j\) 连 \(2E_{i,j}\) 边。
用总收益减最小割。
弱智题不说了。
关于惯性思维：勾股数不一定互质，一个数的勾股数也不唯一配对。
不弱智题，纯靠自己做出来的，开心。
其实得益于上文happiness的经验积累。那道题在相同种类时有combo，这道题不同时有combo，那么可以考虑那道题造辅助点的思路。
我们直接考虑对矩阵黑白染色，黑点的\(S->p->T\) 链接 \(A_i,B_i\) 边，白点则链接 \(B_i,A_i\) 边，同样超原开辅助点连 \(C_{i,j}\)，辅助点往对应点连无穷即可。
黑白染色相当于给每个点交叉了一下，不同就转化为相同了。
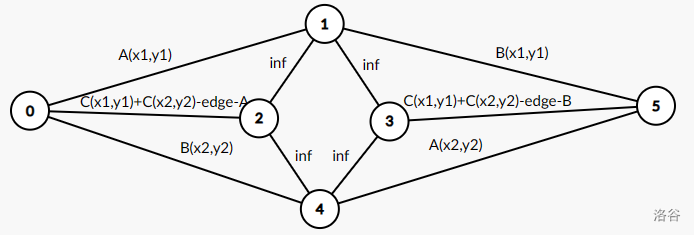
最小割树的东西今没太心思学。开费用流去了。
费用流
（不知道为什么大家不爱用更快的dinic费用流）
建图容易，但是改费用流板子也太呃呃了。以后这种东西板子原理还得再学学的。
纯板题，但是有一些非常诡异的问题。
code 1
add(in(1),out(1),inf,0);
add(in(n),out(n),inf,0);
for(int i=1,u,v,c;i<=m;i++){
scanf("%lld%lld%lld",&u,&v,&c);
add(out(u),in(v),1,c);
}
for(int i=2;i<n;i++)add(in(i),out(i),1,0);
dinic(S,T);
code 2
for(int i=1,u,v,c;i<=m;i++){
scanf("%lld%lld%lld",&u,&v,&c);
add(out(u),in(v),1,c);
}
for(int i=2;i<n;i++)add(in(i),out(i),1,0);
add(in(1),out(1),inf,0);
add(in(n),out(n),inf,0);
两种不同顺序的代码会输出不同的答案且后者会在最后一个随机大点与正确答案差1，我也不知道为什么。
首先为什么他妈后连源汇还是会错啊？？？
以后先连st相关边然后不要相信自己现敲的板子。
其实不是特别好想，一开始想给车拆点，发现按时间拆点不现实。然后是这么个思路，比如师傅 \(i\) 一共修了 \(k\) 辆车，那么倒数第 \(j (j\in[1,k])\) 辆车会给拖延后面 \(j-1\) 辆车各一个 \(T_{i,j}\) 的时间，换句话说就是我们按师傅的修车数给师傅拆点，然后倒数第 \(l\) 辆车的师傅的费用是 \(T_{i,j}*l\)。
这个题很像任务安排的 \(O(n^2)\) 式子的处理方法。
然后就好了，有个傻逼开着8000的n^2ll数组往学校oj交了一万发re。
可以发现是修车那道题的强化。
数据大了不止一点，而且经过一段时间的尝试发现几乎没有新的性质。正解是动态开点优化建图。
因为我们假设每个修车师傅或者厨子都要把车或者菜整完，总数是固定的。所以多开了很多点，如果我们让图更高效就行。
然后涉及到算法原理，这块我确实没太看。第 \(j\) 个厨子加到 \(l\) 层后看一下 \((j,l)\) 这个点用了没，用了就再开一个 \((j,l+1)\) 的点。
至于怎么看：\((j,l)\) 与超原超汇的连边被跑满（或者增广过）。
然后代码放一下因为我不会写。
#include<bits/stdc++.h>
#define MAXN 110005
#define MAXM 2000005
#define N 105
#define int long long
//#define DEBUG wzw
#define loc(i,j) (i-1)*tot+j+n
using namespace std;
int n,m;
struct node{
int v,w,c,nxt;
}edge[MAXM<<1];
int h[MAXN],tmp;
inline void add(int u,int v,int w,int c){
edge[tmp]=(node){u,0,-c,h[v]};
h[v]=tmp++;
edge[tmp]=(node){v,w,c,h[u]};
h[u]=tmp++;
#ifdef DEBUG
printf("%lld - w:%lld,c:%lld -> %lld\n",u,w,c,v);
#endif
}
const int inf=1e18;
int flow,spend;
int top[MAXN],nxt[MAXN];
int p[N],tot,tim[N][N],S,T=MAXN-1;
queue<int >Q;
int dis[MAXN];
bool vis[MAXN];
inline int SPFA(int S,int T){
while(!Q.empty())Q.pop();
fill(dis,dis+MAXN,inf);
dis[S]=0,vis[S]=1;
Q.push(S);
while(!Q.empty()){
int u=Q.front();
Q.pop();
vis[u]=0;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v,w=edge[i].w,c=edge[i].c;
if(dis[v]>dis[u]+c&&w){
dis[v]=dis[u]+c;
if(!vis[v]){
vis[v]=1;
Q.push(v);
}
}
}
}
return dis[T]!=inf;
}
inline int dfs(int u,int minf){
if(u==T||!minf)return minf;
int res=0;
vis[u]=1;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v,w=edge[i].w,c=edge[i].c;
if(dis[v]==dis[u]+c&&w&&!vis[v]){
int ans=dfs(v,min(minf,w));
if(ans){
res+=ans;
minf-=ans;
edge[i].w-=ans;
edge[i^1].w+=ans;
spend+=ans*c;
nxt[u]=v;
if(!minf)break;
}
}
}
if(!res)dis[u]=inf;
vis[u]=0;
return res;
}
inline void dinic(int S,int T){
int res=0;
while(SPFA(S,T)){
res+=dfs(S,inf);
for(int j=1;j<=m;j++){
if(nxt[loc(j,top[j])]&&top[j]<tot){
++top[j];
int u=loc(j,top[j]);
for(int i=1;i<=n;i++)add(i,u,1,tim[i][j]*top[j]);
add(u,T,1,0);
}
}
}
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)scanf("%lld",&p[i]),tot+=p[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
scanf("%lld",&tim[i][j]);
}
}
for(int i=1;i<=n;i++){
add(S,i,p[i],0);
for(int j=1;j<=m;j++)add(i,loc(j,1),1,tim[i][j]);
}
for(int i=1;i<=m;i++){
top[i]=1;
add(loc(i,1),T,1,0);
}
dinic(S,T);
printf("%lld",spend);
return 0;
}
沟槽的码力题。
关于最大权闭合子图问题：感觉就是最小割的标准题型啊（bushi，有常用处理方法是正权给一边求和，负权拉到另一边取正，和-最小割即为答案。
比较易懂感性理解。没负权建不了图咋办？哥没负权了你全拿走输出和不就行了...
然后说这道题：
首先右边的植物人能护住左边的植物人，你想把左边的植物人打死得先打死右边的，右边往左边连边。
然后一个植物人能攻击到的植物人没法打，起码你得先把这个植物人拆掉，连边。
然后你会发现植物人靠这两种做法官官相护可以卡无敌，环和他的外向基环树全无敌，先跑一遍拓扑给这些无敌点扔掉。
然后咱们现在连的边都是无穷边，因为题目是这么规定的，你不能切断他们的保护关系。
然后按照他们的权值正负来给超原超汇连边。超原连正，超汇连负。
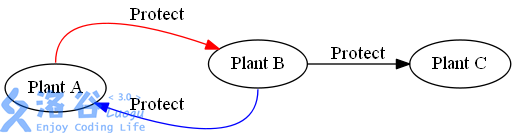
最大权闭合子图问题，颓的，说一下连边。
这个每一步都很骚了所以一块一块说。
如果只考虑收益的combo而不考虑费用，那么在最大权闭合子图问题中有常用策略（植物大战僵尸那题也用了，这题没反应过来）：正贡献辅助点与超原连，负贡献辅助点和超汇连，全指取反，手玩一下你就会发现这样解决了dinic无法解决负贡献取舍的问题。后来想一下这tm不是最小割的思路吗...越做越菜了还。
然后，辅助点是一段连续区间开的，也就是说辅助点要和每个区间内元素相连，边数爆炸，所以会让辅助点链接区间左右端点，然后这个辅助点再往比自己小的两个区间连无穷边，相当于"取了大区间那小区间也必须取"。
再考虑收费的问题，对于同一个编号的食物形成了一个二次函数，考虑斜率优化，我们把他拆开看，因为平方项和取了多少个没关系，我们开一个辅助点往超汇连 \(m*cost^2\) 边，所有这个编号的食物往这个辅助点连无穷边，就实现了"只要点这个编号就必须掏且仅掏一次钱"，然后一次项就再开一个辅助点（其实也可以直接用超汇）让食物点往辅点连 \(cost\) 边，辅助点往超汇连一条无穷边即可。
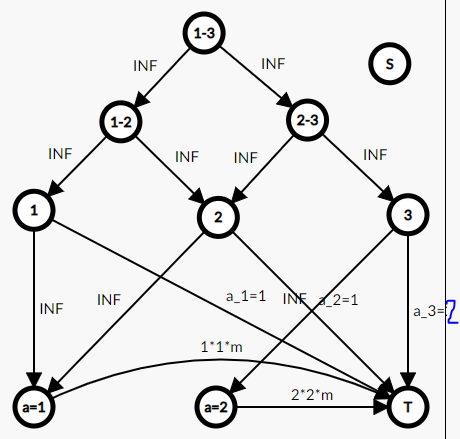
题解区唯一的图，但是贡献的正反没画进去（画进去太乱了）。
这就是个费用流题吧，每个点都要进出 \(v_i\) 次，拆个点，然后有 \(m\) 次无花费进入的机会拿一个辅点维护，剩下的按图和费用链接就行。
然后想让的做法是上下界最小费用流。还是拆点相当于出入点的连边至少要经过 \(v_i\) 次，给个下界，然后跑就可以了。
每个剧情都要跑一次所以每个剧情边有一个1的下界。累加建好边之后给每个点往1点连无穷边相当于重开。
在这个图上跑费用流，加上一开始下界求得和即答案。
说是叫有源汇上下界最小流。
这种题有专门的处理方法，就是在超源超汇的基础上开一个假的源汇。这个假的源汇和一般问题里的超源汇差不多，但是是用来平衡流量的，先跑一边最大流，然后链接这个假的源汇中的汇->源，再在残量网络里跑一次最大流，然后这条平衡边的反边就是需要的最小代价，挺神奇的。
其实不好做，但是建图和80人一样，被秒了。
沟槽的码力题。又难又码。也确实事牛逼题。
题面看完基本没有思路，太怪了。最开始想的还是二分最大流。
拿到题解逆向工程分析思路：显然独立的接口只会出现在格子的交界处，也就是相邻格子才会造成可行性影响，既然如此就可以黑白染色。把每个格子拆成上下左右四个点，根据管子类型连接到这个点，然后相邻格子的相邻上下左右点也相连。
这样在旋转之后给每个黑格端口开一个流，跑最大流到白格看看满不满就能知道可行性了。
然后处理旋转的问题，我们肯定不能真的去旋转的，看看能不能用网络流拟合旋转的过程。
比如这样的右上管道，如果我们顺时针旋转90°那么他就会变成右下管道。
变幻的过程可以把原有的点连到新出现的点，然后！费用就是1。在这里相当于把上点连一个 \(w=1,c=1\) 到下点。别的同理。太妙了。
然后旋转180度费用是2，这种L型管道不用建那个2边，因为两个1边都走正好会变成180的样子。
这就能解释I型管道为什么不能旋转了，这游戏我玩过是能旋转的，原因在于I管一旋转就不太能拿网络流处理了。
所以！这个么个图跑最小费用最大流，验一下流输出费用即可。
可以看出这两题都是最小割板子，但是巨大的点数和连边会导致tle，所以说一下对偶图解决最小割的解法。
文章传送门
把题目给你的图转成对偶图，然后在 \(S',T'\) 上跑一个最短路，这个最短路就是最小割，堆优化dij可以把dinic的玄学复杂度优化到 \(O(nlog^2n)\)。
这里说一下网络流中如何处理一盖多问题。
这个很久以前就开始想了，辅助点就算，这道题提供了个新思路（感觉比较特化），按天数连边处理，这个容量给成 \(inf-a_i\)，费用为0，然后给人从 \(s->t+1\)，费用为 \(c\)，S连第1天，第n+1天连T，容量无穷。
这样会形成一个什么效果，第一次选择最小花费增广的时候会把我们非常鬼畜的天数边尽量跑满，然后所有天数边的余量会变为 \(a_{max}-a_i\)。由于我们跑的是最小费用最大流，那剩下的这点流量在T的时候是必须要跑满的，此时就要用刚才连的带费用边补足。手玩一下就会发现你的dinic自己帮你跑了最优的选人方案。挺神奇的建图。
做完发现发明了01分数规划。
答案式子可以化。
最大化C，显然答案有单调性，考虑二分。
这里面的 \(a_i,b_i\) 是要我们自己取的，硬试肯定不行，发现可以转化为费用流模型：因为最后一定是要配 \(n\) 对的，超源往男点连 \(w=1,c=0\) 边，女点往超汇连 \(w=1,c=0\) 边，男女随便连1边，然后就可以用费用来处理上面的式子，在二分C的基础上一个 \((i,j)\) 配对的费用就是 \(a_{i,j}-Cb_{i,j}\)。跑最大费用最大流验C即可。
老C不喜欢的块里随便捏一个方块他就喜欢了，这种一断全断的模型可以用初中物理电学的方法把不喜欢块里的点串起来跑最小割...
所以就出现了一个显然的做法，拆出入点连代价边，暴力扫所有特殊边左（右）边的那个方块，扫到了就往周围看能不能组成老C不喜欢的块，然后把四个方块连inf起来，跑一个最小割。
然后T飞了，通过一些手段我们发现加入了巨量的重复边，这个重复边的意思不是重边，只是在别的边的作用下它起不到约束作用。
再看看特殊边和老C不喜欢块的关系，我们发现，在一些染色下，不喜欢的块总是经过坐标系中的四个固定颜色。这里引用tj区一张图。
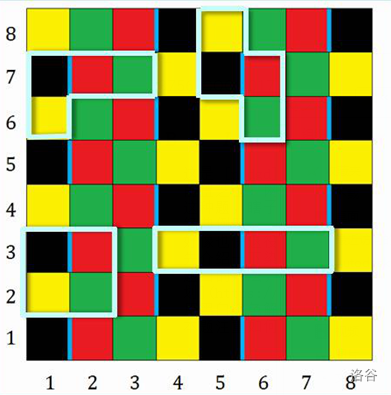
在块点的串联中一定存在连接方案使得经过颜色正好为黄黑红绿。
所以我们按照这种方法给图染色，然后令超源连接到黄点，绿点连接到超汇。然后还是扫所有点，按颜色查四联通方块的颜色，黄连黑黑连红红连绿即可。容易得到每个边都有实际作用。
镜面通道
水能过光就能过，我觉得扯淡，但好像挺对。验相交跑最小割，水。
这个挺难的，前几天板刷直接被击败了。你为什么不是黑。
combo太蛋疼，然后我懒得写了，设一个传送门，有事看tj。
