基环树小结
基环树就是根节点基于环生长的一棵树，特点是 \(n\) 个节点 \(n\) 条边。
如果 \(n\) 个节点 \(n\) 条边的图不联通那么是一个基环森林。
很好证明，\(n\) 个点 \(n-1\) 条边的联通图仅能是一棵树，现在从任一点引出一条边到任一点，由于两点先前一定联通，则在连接后原路径上的任意两点均有两条道路到达，于是形成了环。
对于有向图则为没有父亲节点的根节点又引出一条边指向儿子，则原来的根于儿子形成环。
可以把其归为树上问题的衍生形式，因为现在没有根节点了，所以把这个环当成根节点，不过在处理最优问题时这个环会带来一些麻烦，所以核心就是怎么处理环，处理方法是多样的，没有固定算法。
如果讨厌关系形成了一棵树，那么这道题就是 没有上司的舞会。不过现在形成了一个基环森林，考虑如何处理环的问题。
显然不能直接将子树答案和环上答案相加，因为会出现取舍矛盾的问题。
注意到一个人和他讨厌的人不能同时存在。我们不妨先在图上跳父亲，那么迟早会跳到环里，找到再次相遇时的节点 \(u\) 和他的父亲 \(fa\)，则 \(u\) 与 \(fa\) 肯定不能同时存在。
所以现在考虑将 \(E(u,fa)\) 拆开，形成两棵树 \(V_1,V_2\)，\(root_{V_1}=u,root_{V_2}=fa\)，那么这颗基环树的答案 \(ans=max(ans_{V_1},ans_{V_2})\)。
在 \(u\) 作树根的 \(V_1\) 中，我们让 \(u\) 强制不取，\(fa\) 作为一个叶子结点，出于其父亲的取舍，\(fa\) 的取舍是可以任意的，令 \(dp_{u,1/0}\) 表示节点 \(u\) 取或不取的最优解，为了避免强制不取的根节点会答案的潜在影响，在第一次返祖时令 \(dp_{root,1}=-inf\)。
然后就是正常推式子。
跑一遍 树形 dp。
#include<bits/stdc++.h>
#define MAXN 1000005
#define int long long
using namespace std;
const int inf=1e18;
int n;
struct EDGE{
int v,nxt;
}edge[MAXN];
int h[MAXN],tmp;
int val[MAXN],fa[MAXN];
bool vis[MAXN];
inline void add(int u,int v){
edge[++tmp].v=v;
edge[tmp].nxt=h[u];
h[u]=tmp;
}
int dp[2][MAXN],root,ans;
inline void dfs(int u){
dp[0][u]=0,dp[1][u]=val[u];
vis[u]=1;
for(int i=h[u];i;i=edge[i].nxt){
int v=edge[i].v;
if(v==root)dp[1][root]=-inf;
else{
dfs(v);
dp[0][u]+=max(dp[0][v],dp[1][v]);
dp[1][u]+=dp[0][v];
}
}
}
inline void solve(int u){
vis[u]=1;
root=u;
while(!vis[fa[root]]){
root=fa[root];
vis[root]=1;
}
dfs(root);
int v1=max(dp[0][root],dp[1][root]);
root=fa[root];
dfs(root);
int v2=max(dp[0][root],dp[1][root]);
ans+=max(v1,v2);
}
signed main(){
scanf("%lld",&n);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&val[i],&fa[i]);
add(fa[i],i);
}
for(int i=1;i<=n;i++)if(!vis[i])solve(i);
printf("%lld",ans);
return 0;
}
所以现在出现了一种比较常规的处理方法就是跳父亲找环。
这个题挺烦的，给出的图可能是树，可能是基环树。
既然字典序要最小，那么贪心策略，对联通的节点出度排序，从 1 顺着跑一遍 dfs 肯定是正解。
然后考虑怎么处理基环树，相当于找到环以后，暴力断开环上的边，从两端点作根跑 dfs，时间复杂度 \(O(n^2)\)。
那么如何存环？
给定的图是有向图时，处理是简单的，我们在跳父亲时给节点依次入栈，找到环了一直弹栈到环末为止。
在无向图中就得边 dfs 边判环了，不过具体操作我也没想明白，我又整了一种方法。
既然这是无向图，那么我们可以手动给他搞成有向的，先用 dfs 找环，找到之后直接从那个节点开始跑一遍 树剖dfs1，处理出节点深度以后就相当于是钦定了父亲了，然后按照有向图乱搞就能方便很多。
码子我没写就不放了。
题意翻译成人话：求一个基环森林中每棵基环树的最长链之和。
再出于贪心策略，我们知道这个最长链一定经过了两个环上子树与一条环上的链。
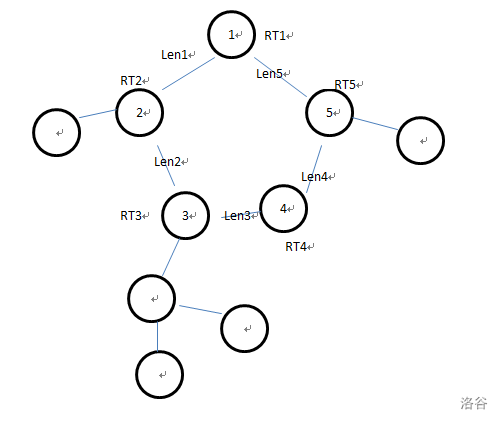
其中 \(rt_i\) 指的是基环树中以环上节点 \(i\) 引导的子树最长链，\(len_i\) 指的是第 \(i\) 个环上节点到第 \(i+1\) 的路径。
我们从节点 1 沿着环逆时针跑，会发现第 \(i\) 个节点的贡献 \(val_i=rt_i+\sum_{1}^{i} len\)，是不变且能处理出最优的。且随着起始点的变化，答案的优先度不会发生改变(所有 val 同增同减)。
然后这个题就做出来了。
不过还有很多细节要处理，如果 \(val_{max}\) 与 \(rt_{max}\) 下标正好相等就得再拿他俩分别比较第二优的 \(rt,val\) 取极值，然后环正反跑是有不同答案的，说着容易写出来细节爆炸。
所以就提出了单调队列写法，即存储优先度递减的待选解，能好做点，不过还是细节爆炸。
我的码调炸了，就不放了。
