树链剖分小结

机房新来了一堆小孩，吵得要死，想把他们剁了。

板题

树剖核心：将树拆分为多个不相交的链，使用数据结构(线段树等)维护修改查询操作。

概念：

• 重儿子：子树根节点的儿子中，以这些儿子为根的子树节点数最多的那个儿子。
• 轻儿子：子树根节点的儿子中，除了重儿子以外的儿子。
• 重边：连接节点与其重儿子的边。
• 轻边：连接节点与其轻儿子的边。
• 重链：重边相连形成的链。

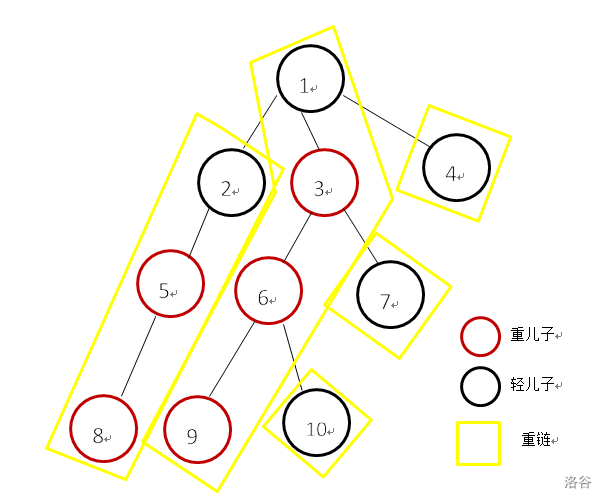
划分重链时需要两遍 \(dfs\)。

\(dfs_1\) 处理：

1. 点深度 \(dep_i\)。
2. 点父亲 \(father_i\)
3. 该点为根节点的子树大小 \(siz_i\)，这顺带是本题 3，4 操作需要的。
4. 每个点的重儿子下标 \(son_i\)

实现和 \(lca\) 的预处理几乎一样。

void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	father[u]=fa;
	siz[u]=1;
	int mson=-1;//重儿子为根节点的子树大小。
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];//统计子树大小。
		if(siz[v]>mson)mson=siz[v],son[u]=v;//选举重儿子，很好理解。
	}
}

\(dfs_2\) 处理：

1. 每个点的 \(dfs\) 序，也就是 \(dfn_i\)，这个值也是新点的编号。
2. 给新点赋值。当然有的题可能没有初值就不用给了。
3. 当前点所属链的顶点 \(top_i\)

对点的遍历优先跑重儿子再跑轻儿子，至于为啥之后解释。

void dfs2(int u,int topf){
	dfn[u]=++tim;//有点像tarjan，反正这些东西思想差不多。
	rk[tim]=v[u];
	top[u]=topf;//处理该点顶点。
	if(!son[u])return;//叶子结点就不用再搜了。
	dfs2(son[u],topf);//优先处理重儿子，也就是重链，此时顶点不变。
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);//处理轻儿子，此时是一条新链，更新一下顶点。
	}
}

\(dfs\) 序的优秀性质使得这些点可以使用屎山线段树优化。又因为我们是优先处理重儿子的，所以同一条链内两点的 \(dfn\) 所形成的区间正好就是两点间的路径。解释了上问的问题。

我们拉一泡写一棵线段树出来。

struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	#define push_up(p) tree[p].val=((tree[leftson(p)].val+tree[rightson(p)].val)%P+P)%P
	struct TREE{
		int l,r;
		int val,tag;
	}tree[MAXN<<2];
	void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].tag=0;
		if(l==r){
			tree[p].val=rk[l]%P;
			return;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].val=((tree[leftson(p)].val+tree[p].tag*(tree[leftson(p)].r-tree[leftson(p)].l+1)%P)%P+P)%P;
			tree[rightson(p)].val=((tree[rightson(p)].val+tree[p].tag*(tree[rightson(p)].r-tree[rightson(p)].l+1)%P)%P+P)%P;
			tree[leftson(p)].tag=((tree[leftson(p)].tag+tree[p].tag)%P+P)%P;
			tree[rightson(p)].tag=((tree[rightson(p)].tag+tree[p].tag)%P+P)%P;
			tree[p].tag=0;
		}
	}
	void update(int l,int r,int k,int p){
		if(tree[p].l>=l&&tree[p].r<=r){
			tree[p].val=((tree[p].val+k*(tree[p].r-tree[p].l+1)%P)%P+P)%P;
			tree[p].tag=((tree[p].tag+k)%P+P)%P;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
	//	printf("l:%lld r:%lld tl:%lld tr:%lld mid:%lld\n",l,r,tree[p].l,tree[p].r,mid);
		if(l<=mid)update(l,r,k,leftson(p));
		if(r>mid)update(l,r,k,rightson(p));
		push_up(p);
	}
	int query(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val%P;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=0;
		if(l<=mid)res=(res+query(l,r,leftson(p))%P)%P;
		if(r>mid)res=(res+query(l,r,rightson(p))%P)%P;
		return (res%P+P)%P;
	}
}ST;

预处理好后解决以下问题：

• 将树从 \(x\) 节点到 \(y\) 节点的最短路径上的所有节点值加 \(z\)。
• 求树从 \(x\) 节点到 \(y\) 节点的最短路径上的点权和。
• 将以 \(x\) 为根节点的子树的所有点权加 \(z\)
• 求以 \(x\) 为根节点的子树的点权和。

处理任务 1，2 时，可以使用类似 \(lca\) 的处理方法。不过要基于重链来处理。

具体地：规定点 \(x,y\) 所属重链顶端节点为 \(f_x,f_y\)，处理每个节点的深度 \(dep[i]\)，不妨设 \(dep_{f_x}>dep_{f_y}\) 则点权和 \(res\) 应加上点 \(x\) 到 \(f_x\) 路径上的点权和，\(x\) 变为 \(f_x\) 的父亲。重复此过程只到 \(x,y\) 共 \(f\)。此时加上两点间的点权和。

例图中：求 \((8,7)\) 的点权和：

• \(dep_{f_7}<dep_{f_8}\)，故点 \(x\) 由 \(8\) 变为 \(f_2=1\)，\(res=res+\sum_{i\in{HeavyPath_2}}{val_i}\)。
• \(dep_{f_1}<dep_{f_7}\)，故点 \(x\) 由 \(7\) 变为 \(f_7=3\)，\(res=res+\sum_{i\in{HeavyPath_7}}{val_i}\)。
• \(f_1=f_3,res=res+val_1+val_3\)

修改是一个道理，将线段树的查询操作改为修改操作即可。

	inline int qrange(int x,int y){
		int ans=0;
		while(top[x]!=top[y]){//不共链就一直跳
			if(dep[top[x]]<dep[top[y]])swap(x,y);//找所在链顶点更深的点
			int res=ST.query(dfn[top[x]],dfn[x],1);
			ans=((ans+res)%P+P)%P;//加入顶点更深链的权值
			x=father[top[x]];//跳父亲
		}
		if(dep[x]>dep[y])swap(x,y);
		int res=ST.query(dfn[x],dfn[y],1);
		ans=((ans+res)%P+P)%P;//同链后规定深度先后，加上两点间路径的权值
		return ans;
	}
	inline void uprange(int x,int y,int k){
		k%=P;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ST.update(dfn[top[x]],dfn[x],k,1);
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		ST.update(dfn[x],dfn[y],k,1);//同上，求和改为修改即可。
	}

至于 3,4 的子树操作：

\(dfs\) 中，自点 \(i\) 开始的 \(siz[i]\) 个点都属于 \(i\) 自己和其儿子。他们的 \(dfn\) 也是连续的，所以一棵子树 \(i\) 的点编号是 \(i\sim i+siz[i]-1\)。

	inline int qson(int x){
		return ST.query(dfn[x],dfn[x]+siz[x]-1,1)%P;
	}
	inline void upson(int x,int k){
	//	printf("x=%lld,rank=%lld siz[%lld]:%lld\n",x,rank[x],x,siz[x]);
		ST.update(dfn[x],dfn[x]+siz[x]-1,k,1);
	}

然后是完整代码。

#include<bits/stdc++.h>
#define int long long
#define MAXN 100005
using namespace std;
int n,m,root,P;
int v[MAXN];
vector<int>edge[MAXN];
int dep[MAXN],siz[MAXN],father[MAXN],son[MAXN];
int top[MAXN],dfn[MAXN],tim,rk[MAXN];
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	father[u]=fa;
	siz[u]=1;
	int mson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>mson)mson=siz[v],son[u]=v;
	}
}
void dfs2(int u,int topf){
	dfn[u]=++tim;
	rk[tim]=v[u];
	top[u]=topf;
	if(!son[u])return;
	dfs2(son[u],topf);
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	#define push_up(p) tree[p].val=((tree[leftson(p)].val+tree[rightson(p)].val)%P+P)%P
	struct TREE{
		int l,r;
		int val,tag;
	}tree[MAXN<<2];
	void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].tag=0;
		if(l==r){
			tree[p].val=rk[l]%P;
			return;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].val=((tree[leftson(p)].val+tree[p].tag*(tree[leftson(p)].r-tree[leftson(p)].l+1)%P)%P+P)%P;
			tree[rightson(p)].val=((tree[rightson(p)].val+tree[p].tag*(tree[rightson(p)].r-tree[rightson(p)].l+1)%P)%P+P)%P;
			tree[leftson(p)].tag=((tree[leftson(p)].tag+tree[p].tag)%P+P)%P;
			tree[rightson(p)].tag=((tree[rightson(p)].tag+tree[p].tag)%P+P)%P;
			tree[p].tag=0;
		}
	}
	void update(int l,int r,int k,int p){
		if(tree[p].l>=l&&tree[p].r<=r){
			tree[p].val=((tree[p].val+k*(tree[p].r-tree[p].l+1)%P)%P+P)%P;
			tree[p].tag=((tree[p].tag+k)%P+P)%P;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
	//	printf("l:%lld r:%lld tl:%lld tr:%lld mid:%lld\n",l,r,tree[p].l,tree[p].r,mid);
		if(l<=mid)update(l,r,k,leftson(p));
		if(r>mid)update(l,r,k,rightson(p));
		push_up(p);
	}
	int query(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val%P;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=0;
		if(l<=mid)res=(res+query(l,r,leftson(p))%P)%P;
		if(r>mid)res=(res+query(l,r,rightson(p))%P)%P;
		return (res%P+P)%P;
	}
}ST;
namespace HPD{
	inline int qrange(int x,int y){
		int ans=0;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			int res=ST.query(dfn[top[x]],dfn[x],1);
			ans=((ans+res)%P+P)%P;
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		int res=ST.query(dfn[x],dfn[y],1);
		ans=((ans+res)%P+P)%P;
		return ans;
	}
	inline void uprange(int x,int y,int k){
		k%=P;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ST.update(dfn[top[x]],dfn[x],k,1);
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		ST.update(dfn[x],dfn[y],k,1);
	}
	inline int qson(int x){
		return ST.query(dfn[x],dfn[x]+siz[x]-1,1)%P;
	}
	inline void upson(int x,int k){
	//	printf("x=%lld,rank=%lld siz[%lld]:%lld\n",x,rank[x],x,siz[x]);
		ST.update(dfn[x],dfn[x]+siz[x]-1,k,1);
	}
}
signed main(){
	scanf("%lld%lld%lld%lld",&n,&m,&root,&P);
	for(int i=1;i<=n;i++)scanf("%lld",&v[i]);
	for(int i=1,u,v;i<n;i++){
		scanf("%lld%lld",&u,&v);
		edge[u].push_back(v);
		edge[v].push_back(u);
	}
	dfs1(root,0);
	dfs2(root,root);
	ST.build(1,n,1);
//	for(int i=1;i<=n<<2;i++)printf("tree[%lld]:l=%lld,r=%lld,val=%lld,tag=%lld\n",i,ST.tree[i].l,ST.tree[i].r,ST.tree[i].val,ST.tree[i].tag);
	while(m--){
		int opt,x,y,z;
		scanf("%lld",&opt);
		if(opt==1){
			scanf("%lld%lld%lld",&x,&y,&z);
			HPD::uprange(x,y,z);
		}
		if(opt==2){
			scanf("%lld%lld",&x,&y);
			printf("%lld\n",HPD::qrange(x,y));
		}
		if(opt==3){
			scanf("%lld%lld",&x,&z);
			HPD::upson(x,z);
		}
		if(opt==4){
			scanf("%lld",&x);
			printf("%lld\n",HPD::qson(x));
		}
	}
	return 0;
}

很长，但是好理解，看之后怎么做题了。

这个东西要是题目主要环节，换句话说，题目只让你做树上操作，那就是板题。稍微加点结论，优化那就是紫。要是只作为工具使用那可能就是黑了，那我也不会做。所以列出来的这些都不是特别难。

P2590

敲键盘水题，非常无聊，单点修改，区间极值与和查询。

P2486

比较有意思。

一开始以为是统计颜色种类，就像hh的项链那种。后来发现112211算三段，就会比较好做。

两段答案合并时，当且仅当左边的右端点等于右边的左端点时会出现答案的重复，只需要--ans。这个原则在push_up,query,getans都需要使用，注意一下即可。

#include<bits/stdc++.h>
#define int long long
#define MAXN 100005
using namespace std;
int n,q;
int v[MAXN];
vector<int>edge[MAXN];
int father[MAXN],dep[MAXN],siz[MAXN],son[MAXN];
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	father[u]=fa;
	siz[u]=1;
	int maxson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)son[u]=v,maxson=siz[v];
	}
}
int top[MAXN],dfn[MAXN],rk[MAXN],tim;
void dfs2(int u,int topf){
	dfn[u]=++tim;
	top[u]=topf;
	rk[tim]=v[u];
	if(!son[u])return;
	dfs2(son[u],topf);
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	struct TREE{
		int l,r;
		int lval,rval,tag,num;
	}tree[MAXN<<2];
	void push_up(int p){
		tree[p].lval=tree[leftson(p)].lval;
		tree[p].rval=tree[rightson(p)].rval;
		tree[p].num=tree[leftson(p)].num+tree[rightson(p)].num;
		if(tree[leftson(p)].rval==tree[rightson(p)].lval)--tree[p].num;
		return;
	}
	void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].lval=tree[p].rval=tree[p].num=0;
		if(l==r){
			tree[p].lval=tree[p].rval=rk[l];
			tree[p].num=1;
			return;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].num=tree[rightson(p)].num=1;
			tree[leftson(p)].lval=tree[leftson(p)].rval=tree[rightson(p)].lval=tree[rightson(p)].rval=tree[p].tag;
			tree[leftson(p)].tag=tree[rightson(p)].tag=tree[p].tag;
			tree[p].tag=0;
			return;
		}
	}
	void update(int l,int r,int k,int p){
		if(tree[p].l>=l&&tree[p].r<=r){
			tree[p].lval=tree[p].rval=k;
			tree[p].tag=k;
			tree[p].num=1;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(l<=mid)update(l,r,k,leftson(p));
		if(r>mid)update(l,r,k,rightson(p));
		push_up(p);
	}
	int query(int l,int r,int p){
		if(tree[p].l==l&&tree[p].r==r)return tree[p].num;
		spread(p);
	//	printf("spread\n");
		int mid=tree[p].l+tree[p].r>>1;
		int ans=0;
		if(l>mid)return query(l,r,rightson(p));
		if(r<=mid)return query(l,r,leftson(p));
		else{
			ans=query(l,mid,leftson(p))+query(mid+1,r,rightson(p));
			if(tree[leftson(p)].rval==tree[rightson(p)].lval)--ans;
			return ans;
		}
	}
	int getl(int x,int p){
		if(tree[p].l==tree[p].r)return tree[p].lval;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(x<=mid)return getl(x,leftson(p));
		else return getl(x,rightson(p));
	}
}ST;
namespace HPD{
	void modify(int x,int y,int k){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ST.update(dfn[top[x]],dfn[x],k,1);
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		ST.update(dfn[x],dfn[y],k,1);
	}
	void getans(int x,int y){
		int ans=0;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ans+=ST.query(dfn[top[x]],dfn[x],1);
			if(ST.getl(dfn[father[top[x]]],1)==ST.getl(dfn[top[x]],1))--ans;
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		ans+=ST.query(dfn[x],dfn[y],1);
		printf("%lld\n",ans);
	}
}
signed main(){
	scanf("%lld%lld",&n,&q);
	for(int i=1;i<=n;i++)scanf("%lld",&v[i]);
	for(int i=1,u,v;i<n;i++){
		scanf("%lld%lld",&u,&v);
		edge[u].push_back(v);
		edge[v].push_back(u);
	}
	dfs1(1,0);
	dfs2(1,1);
	ST.build(1,n,1);
	for(int i=1,l,r,val;i<=q;i++){
		char opt;
		cin>>opt;
		if(opt=='Q'){
			scanf("%lld%lld",&l,&r);
			HPD::getans(l,r);	
		}
		if(opt=='C'){
			scanf("%lld%lld%lld",&l,&r,&val);
			HPD::modify(l,r,val);
		}
	}
	return 0;
}

SP375

运用了边权下放到点的技巧。

#include<bits/stdc++.h>
#define int long long
#define MAXN 10005
using namespace std;
int n,T;
struct node{
	int v,w;
};
struct node2{
	int u,v;
}road[MAXN];
vector<node>edge[MAXN];
int Val[MAXN];
int father[MAXN],son[MAXN],siz[MAXN],dep[MAXN];
void dfs1(int u,int fa){
	dep[u]=dep[fa]+1;
	father[u]=fa;
	siz[u]=1;
	int maxson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i].v,w=edge[u][i].w;
		if(v==fa)continue;
		Val[v]=w;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
}
int top[MAXN],tim,dfn[MAXN],rk[MAXN];
void dfs2(int u,int topf){
	dfn[u]=++tim;
	rk[tim]=Val[u];
	top[u]=topf;
	if(!son[u])return;
	dfs2(son[u],topf);
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i].v,w=edge[u][i].w;
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	#define push_up(p) tree[p].val=max(tree[leftson(p)].val,tree[rightson(p)].val)
	struct TREE{
		int l,r;
		int val,tag;
	}tree[MAXN<<2];
	void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].tag=tree[p].val=0;
		if(l==r){
			tree[p].val=rk[l];
			return;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].val=tree[rightson(p)].val=tree[p].tag;
			tree[leftson(p)].tag=tree[rightson(p)].tag=tree[p].tag;
			tree[p].tag=0;
			return;
		}
	}
	void update(int x,int k,int p){
		if(tree[p].l==tree[p].r){
			tree[p].val=tree[p].tag=k;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(x<=mid)update(x,k,leftson(p));
		else update(x,k,rightson(p));
		push_up(p);
	}
	int query(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=0;
		if(l<=mid)res=max(res,query(l,r,leftson(p)));
		if(r>mid)res=max(res,query(l,r,rightson(p)));
		return res;
	}
}ST;
namespace HPD{
	void modify(int id,int val){
		int x=road[id].u,y=road[id].v;
		ST.update(max(dfn[x],dfn[y]),val,1);
		return; 
	}
	void getans(int x,int y){
		int res=0;
		if(x==y){
			printf("0\n");
			return;
		}
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			res=max(res,ST.query(dfn[top[x]],dfn[x],1));
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		if(dfn[x]==dfn[y]){
			printf("%lld\n",res);
			return;
		}
		else{
			res=max(res,ST.query(dfn[x]+1,dfn[y],1));
			printf("%lld\n",res);
		}
	}
}
void INIT(){
	memset(road,0,sizeof(road));
	memset(father,0,sizeof(father));
	memset(son,0,sizeof(son));
	memset(dep,0,sizeof(dep));
	memset(siz,0,sizeof(siz));
	memset(Val,0,sizeof(Val));
	memset(dfn,0,sizeof(dfn));
	memset(top,0,sizeof(top));
	memset(rk,0,sizeof(rk));
	tim=0;
	for(int i=1;i<=n;i++)edge[i].clear();
	memset(ST.tree,0,sizeof(ST.tree));
}
signed main(){
	scanf("%lld",&T);
	while(T--){
		scanf("%lld",&n);
		INIT();
		for(int i=1,u,v,w;i<n;i++){
			scanf("%lld%lld%lld",&u,&v,&w);
			edge[u].push_back({v,w});
			edge[v].push_back({u,w});
			road[i].u=u,road[i].v=v; 
		}	
		dfs1(1,0);
		dfs2(1,1);
		ST.build(1,n,1); 
		string opt;
		while(cin>>opt){
			if(opt=="DONE")break;
			int l,r;
			scanf("%lld%lld",&l,&r);
			if(opt=="QUERY")HPD::getans(l,r);
			if(opt=="CHANGE")HPD::modify(l,r);
		}
	}
	return 0;
}

但是这道题在谷上有bug，就先不交了。

运输答辩

很毒瘤的一道题，因为手滑+眼瞎让一个弱智bug卡了两天。

“清零一条边权”这样的操作对答案的影响是致命的。

最初以为答案只会受两个东西影响：最长查询路径 \(E\) 与不过 \(E\) 最长边 \(E_0\) 的最长路径 \(E'\)。调了半个下午想到 \(E\) 中的每条路径都会导致 \(E'\) 的变化，换句话说，取\(E_0\) 不一定有 \(\{max\{E-E_0,E'\}\}_{min}\)。查看题解发现补集的思想是没有问题的，但是要对 \(E\) 进行逐条边删除。

会导致 \(TLE\)，于是再使用一棵线段树直接维护路径。\(\Theta(n^2)->\Theta(n\ logn)\)

规定 \(ST2.tree[dfn[x]].xval\) 为不经过边 \((fa[x],x)\) 的最大路径。

那么将一条路径剖分后，对于每个小段 \((u_1,v_1)\sim(u_m,v_m),dfn[v_i]>dfn[u_i]\)，将他们按左端点 \(dfs\) 序排好后，小段 \((v_i+1,u_{i+1}-1)\) 是本条路径不经过的段。那么就要更新不经过此段 \((v_i+1,u_{i+1}-1)\) 的最大路径权值 \(val_{(x,y)}\)。最后对于最长路径 \(E\) 每条边 \(E_i\)，规定路径总长为 \(val\) 与不过该边的最长路径 \(val:C_UE_i\) 有：

\[ans=min(max(val-E_i,max\{val:C_UE_i\})) \]

绕死个人。

另外 \((u_1,v_1)\) 的左边可能有一段补集 \((1,u_1-1)\)，\((u_m,v_m)\) 的右边也有可能有一段补集 \((v_m+1,n)\)。特判即可。

注意到答案式子中出现了极小极大值状物，这个题肯定是可以二分答案的，有时间再写一写。

#include<bits/stdc++.h>
#define int long long
#define MAXN 300005
using namespace std;
int n,q;
struct node{
	int v,w;
};
vector<node>edge[MAXN];
int father[MAXN],son[MAXN],dep[MAXN],siz[MAXN];
int Val[MAXN];
void dfs1(int u,int fa){
	father[u]=fa;
	dep[u]=dep[fa]+1;
	siz[u]=1;
	int maxson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i].v,w=edge[u][i].w;
		if(v==fa)continue;
		Val[v]=w;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
}
int top[MAXN],dfn[MAXN],rk[MAXN],tim;
void dfs2(int u,int topf){
	top[u]=topf;
	dfn[u]=++tim;
	rk[tim]=Val[u];
	if(!son[u])return;
	dfs2(son[u],topf);
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i].v;
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
namespace RMS{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	struct Segment_Tree_Range{
		struct TREER{
			int l,r;
			int val,xval;
		}tree[MAXN<<2];
		void push_up(int p){
			tree[p].xval=max(tree[leftson(p)].xval,tree[rightson(p)].xval);
			tree[p].val=tree[leftson(p)].val+tree[rightson(p)].val;
			return;
		}
		void build(int l,int r,int p){
			tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].xval=0;
			if(tree[p].l==tree[p].r){
				tree[p].val=tree[p].xval=rk[l];
				return;
			}
			int mid=l+r>>1;
			build(l,mid,leftson(p));
			build(mid+1,r,rightson(p));
			push_up(p);
		}
		int xquery(int l,int r,int p){
			if(tree[p].l>=l&&tree[p].r<=r)return tree[p].xval;
			int mid=tree[p].l+tree[p].r>>1;
			int res=0;
			if(l<=mid)res=max(res,xquery(l,r,leftson(p)));
			if(r>mid)res=max(res,xquery(l,r,rightson(p)));
			return res;
		}
		int valquery(int l,int r,int p){
			if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val;
			int mid=tree[p].l+tree[p].r>>1;
			int res=0;
			if(l<=mid)res+=valquery(l,r,leftson(p));
			if(r>mid)res+=valquery(l,r,rightson(p));
			return res;
		}
	}ST1;
	struct Segment_Tree_Edge{
		struct TREEE{
			int l,r;
			int tag,xval;
		}tree[MAXN<<2];
		void push_up(int p){
			tree[p].xval=max(tree[leftson(p)].xval,tree[rightson(p)].xval);
			return;
		}
		void build(int l,int r,int p){
			tree[p].l=l,tree[p].r=r,tree[p].tag=tree[p].xval=0;
			if(l==r)return;
			int mid=tree[p].l+tree[p].r>>1;
			build(l,mid,leftson(p));
			build(mid+1,r,rightson(p));
			push_up(p);
		}
		void spread(int p){
			if(tree[p].tag){
				tree[leftson(p)].xval=max(tree[leftson(p)].xval,tree[p].tag);
				tree[rightson(p)].xval=max(tree[rightson(p)].xval,tree[p].tag);
				tree[leftson(p)].tag=max(tree[leftson(p)].tag,tree[p].tag);
				tree[rightson(p)].tag=max(tree[rightson(p)].tag,tree[p].tag);
				tree[p].tag=0;
				return;
			}
		}
		void update(int l,int r,int k,int p){
			if(tree[p].l>=l&&tree[p].r<=r){
				tree[p].xval=max(tree[p].xval,k);
				tree[p].tag=max(tree[p].tag,k);
				return;
			}
			spread(p);
			int mid=tree[p].l+tree[p].r>>1;
			if(l<=mid)update(l,r,k,leftson(p));
			if(r>mid)update(l,r,k,rightson(p));
			push_up(p);
		}
		int query(int x,int p){
			if(tree[p].l==tree[p].r)return tree[p].xval;
			spread(p);
			int mid=tree[p].l+tree[p].r>>1;
			if(x<=mid)return query(x,leftson(p));
			else return query(x,rightson(p));
		}
	}ST2;
}
int maxval,ku,kv;
namespace HPD{
	int lid[MAXN],rid[MAXN],ne[MAXN];
	bool cmp(int a,int b){
		return lid[a]<lid[b];
	}
	int getval(int x,int y){
		int res=0;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			res+=RMS::ST1.valquery(dfn[top[x]],dfn[x],1);
			x=father[top[x]];
		}
		if(dep[x]==dep[y])return res;
		if(dep[x]>dep[y])swap(x,y);
		res+=RMS::ST1.valquery(dfn[x]+1,dfn[y],1);
		return res;
	}
	void update(int x,int y,int k){
		int tmp=0;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			lid[++tmp]=dfn[top[x]],rid[tmp]=dfn[x];
			x=father[top[x]];
		}
		if(dfn[x]>dfn[y])swap(x,y);
		lid[++tmp]=dfn[x]+1,rid[tmp]=dfn[y];
		for(int i=1;i<=tmp;i++)ne[i]=i;
		sort(ne+1,ne+1+tmp,cmp);
		if(lid[ne[1]]>1)RMS::ST2.update(1,lid[ne[1]]-1,k,1);
		if(rid[ne[tmp]]<n)RMS::ST2.update(rid[ne[tmp]]+1,n,k,1);
		for(int i=1;i<tmp;i++)RMS::ST2.update(rid[ne[i]]+1,lid[ne[i+1]]-1,k,1);
		return;
	}
	int getans(int x,int y){
		int ans=1e18;
		if(x==y)return 0;
		if(dep[x]<dep[y])swap(x,y);
		while(dep[x]!=dep[y]){
			ans=min(ans,max(maxval-Val[x],RMS::ST2.query(dfn[x],1)));
			x=father[x];
		}
		while(x!=y){
			if(dep[x]<=dep[y])swap(x,y);
			ans=min(ans,max(maxval-Val[x],RMS::ST2.query(dfn[x],1)));
			x=father[x];
		}
		return ans;
	}
}
signed main(){
	scanf("%lld%lld",&n,&q);
	for(int i=1,u,v,w;i<n;i++){
		scanf("%lld%lld%lld",&u,&v,&w);
		edge[u].push_back({v,w});
		edge[v].push_back({u,w});
	}	
	dfs1(1,0);
	dfs2(1,1);
	RMS::ST1.build(1,n,1);
	RMS::ST2.build(1,n,1);
	for(int i=1,u,v;i<=q;i++){
		int val=0;
		scanf("%lld%lld",&u,&v);
		val=HPD::getval(u,v);
		HPD::update(u,v,val);
		if(val>maxval)maxval=val,ku=u,kv=v;
	}
	printf("%lld",HPD::getans(ku,kv));
	return 0;
}

遥远国度

出现了神秘的换根操作。

其他的都是板子，不解释。

题解其实都说麻烦了。提供一个只需要很少讨论的方案。

• 首先 \(dfs\) 序与深度是没必要修改的，也没有时间成本去修改。
• 查询子树就是树根，直接输出 \(ans_{(1,n)}\)
• 查询子树的深度深于当前根的深度，子树没有变化，输出 \(ans_{(dfn[x],dfn[x]+siz[x]-1)}\)
• 查询子树的深度浅于当前根。如果根到祖先节点 1 的路径上有该节点：

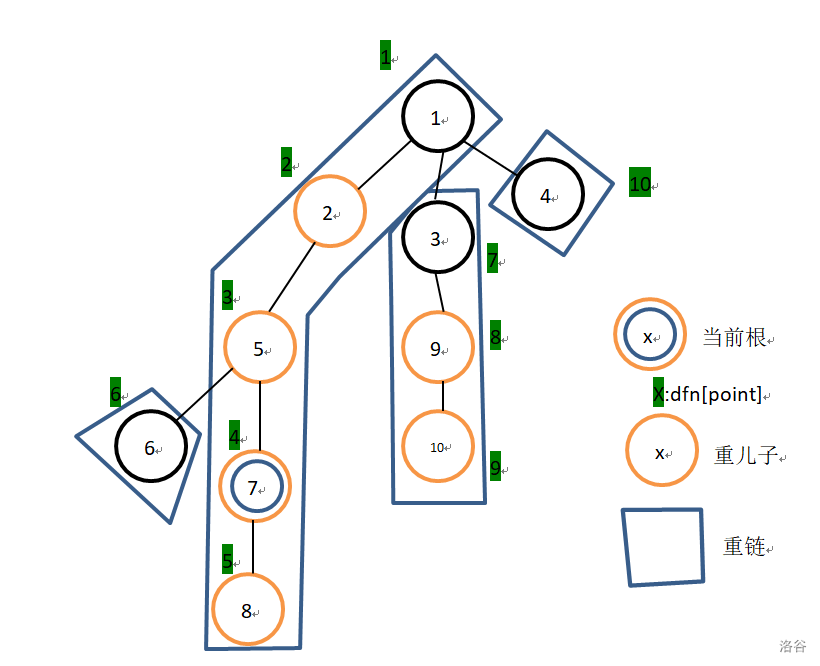
如果我们要查询节点 5，那么此时 5 的儿子（包括自己）集合 \(E=\{5,6,2,1,3,9,10,4\}\)。至于为什么要用 5 举例，坑点在于 5 的轻儿子 6 也算当前情况下 5 子树的一部分。换句话说，不能覆盖的区间是当前点直系儿子的子树。

	int lca(int x,int y){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			x=father[top[x]];
		}
		if(x==y)return x;
		if(dep[x]>dep[y])swap(x,y);
		return x;
	}
	...
		if(dep[x]<dep[root]&&lca(x,root)==x){
			int fa=son[x];
			return min(ST.query(1,dfn[x],1),ST.query(dfn[fa]+siz[fa],n,1));
		}   

很茫然地获得70pts

其实要在 lca 时直接求出那个儿子。并且上文所说的是 直系儿子 而不是 重儿子 。为什么呢？

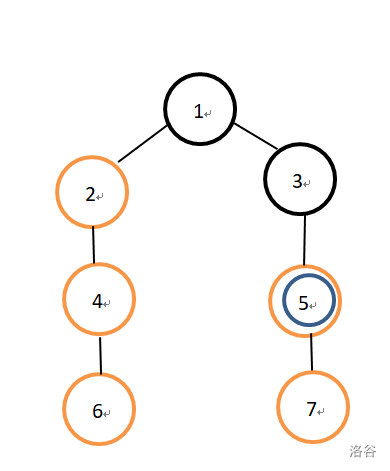
当前情况下，如果我们查询 1 节点子树理应是 \(E=\{1,2,4,6\}\)。然而因为预处理的问题，虽然节点 2 与节点 3 有同样的子树大小，重儿子被选举成了 2。这导致查询节点 1 时实际查询的子树 \(E'=\{1,3,5,7\}\)。换句话说， 儿子必须要在路径 \((x,root)\)上。

namespace HPD{
	int lca(int x,int y){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			if(father[top[x]]==y)return top[x];
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		return son[x];
	}
	...
	int getans(int x){
		...
		if(dep[x]<dep[root]&&father[lca(x,root)]==x){
			int fa=lca(x,root);
			return min(ST.query(1,dfn[fa]-1,1),ST.query(dfn[fa]+siz[fa],n,1));
		}
        
}

我们最终选择用 lca 函数求那个直系儿子，很多情况下我们不需要返回重儿子，而是发现 x 顶点父亲就是 y 后直接返回顶点，这样儿子肯定是在路径上的。返回重儿子，当且仅当已经确定 x,y 共链。 这个真的非常重要。

另外我们少讨论了一种情况：

• 查询子树深度浅于当前根，如果当前节点不在 \((root,1)\) 的路径上，那么对答案完全没有影响。

这是完整代码。

#include<bits/stdc++.h>
#define int long long
#define MAXN 100005
using namespace std;
int n,q;
vector<int>edge[MAXN];
int root,Val[MAXN];
const int inf=1e18;
int father[MAXN],son[MAXN],dep[MAXN],siz[MAXN];
void dfs1(int u,int fa){
	father[u]=fa;
	dep[u]=dep[fa]+1;
	siz[u]=1;
	int maxson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==fa)continue;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
}
int dfn[MAXN],top[MAXN],rk[MAXN],tim;
void dfs2(int u,int topf){
	dfn[u]=++tim;
	rk[tim]=Val[u];
	top[u]=topf;
	if(!son[u])return;
	dfs2(son[u],topf);
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(v==father[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	#define push_up(p) tree[p].val=min(tree[leftson(p)].val,tree[rightson(p)].val)
	struct TREE{
		int l,r;
		int val,tag;
	}tree[MAXN<<2];
	void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].val=inf,tree[p].tag=0;
		if(l==r){
			tree[p].val=rk[l];
			return;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].val=tree[rightson(p)].val=tree[p].tag;
			tree[leftson(p)].tag=tree[rightson(p)].tag=tree[p].tag;
			tree[p].tag=0;
			return;
		}
	}
	void update(int l,int r,int k,int p){
		if(tree[p].l>=l&&tree[p].r<=r){
			tree[p].val=tree[p].tag=k;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(l<=mid)update(l,r,k,leftson(p));
		if(r>mid)update(l,r,k,rightson(p));
		push_up(p);
	}
	int query(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=inf;
		if(l<=mid)res=min(res,query(l,r,leftson(p)));
		if(r>mid)res=min(res,query(l,r,rightson(p)));
		return res;
	}
}ST;
namespace HPD{
	int lca(int x,int y){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			if(father[top[x]]==y)return top[x];
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		return son[x];
	}
	void modify(int x,int y,int k){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ST.update(dfn[top[x]],dfn[x],k,1);
			x=father[top[x]];
		}
		if(dep[x]>dep[y])swap(x,y);
		ST.update(dfn[x],dfn[y],k,1);
		return;
	}
	int getans(int x){
		if(x==root)return ST.query(1,n,1);
		if(dep[x]>=dep[root])return ST.query(dfn[x],dfn[x]+siz[x]-1,1);
		if(dep[x]<dep[root]&&father[lca(x,root)]==x){
			int fa=lca(x,root);
			return min(ST.query(1,dfn[fa]-1,1),ST.query(dfn[fa]+siz[fa],n,1));
		}
		else return ST.query(dfn[x],dfn[x]+siz[x]-1,1);
	}
}
signed main(){
	scanf("%lld%lld",&n,&q);
	for(int i=1,u,v;i<n;i++){
		scanf("%lld%lld",&u,&v);
		edge[u].push_back(v);
		edge[v].push_back(u);
	}	
	for(int i=1;i<=n;i++)scanf("%lld",&Val[i]);
	scanf("%lld",&root);
	dfs1(root,0);
	dfs2(root,root);
	ST.build(1,n,1);
	for(int i=1,opt,id,x,y,z;i<=q;i++){
		scanf("%lld",&opt);
		if(opt==1){
			scanf("%lld",&id);
			root=id;
		}
		if(opt==2){
			scanf("%lld%lld%lld",&x,&y,&z);
			HPD::modify(x,y,z);
		}
		if(opt==3){
			scanf("%lld",&id);
			printf("%lld\n",HPD::getans(id));
		}
	}
	return 0;
}

旅游

大码力水题，我就喜欢这种看题思考一分钟然后全程敲爆键盘的感觉。

运用了边权下放到点，区间求和求极值，单点修改与区间取反。

有个坑是取反一次再取反相当于没取反，打 \(tag\) 时注意用到异或。

#include<bits/stdc++.h>
#define MAXN 200005
using namespace std;
int n,q;
const int inf=1e9;
struct node{
	int v,w;
};
vector<node> edge[MAXN];
int Val[MAXN];
int dep[MAXN],father[MAXN],son[MAXN],siz[MAXN];
inline void dfs1(int u,int fa){
	father[u]=fa;
	dep[u]=dep[fa]+1;
	siz[u]=1;
	int maxson=-1;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i].v,w=edge[u][i].w;
		if(v==fa)continue;
		Val[v]=w;
		dfs1(v,u);
		siz[u]+=siz[v];
		if(siz[v]>maxson)maxson=siz[v],son[u]=v;
	}
	return;
}
int dfn[MAXN],top[MAXN],rk[MAXN],tim;
inline void dfs2(int u,int topf){
    dfn[u]=++tim;
    rk[tim]=Val[u];
    top[u]=topf;
    if(!son[u])return;
    dfs2(son[u],topf);
    for(int i=0;i<edge[u].size();i++){
        int v=edge[u][i].v;
        if(v==father[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
struct Segment_Tree{
	#define leftson(p) p<<1
	#define rightson(p) p<<1|1
	struct TREE{
		int l,r;
		int val,xval,nval;
		int tag;
	}tree[MAXN<<2];
	inline void push_up(int p){
		tree[p].val=tree[leftson(p)].val+tree[rightson(p)].val;
		tree[p].xval=max(tree[leftson(p)].xval,tree[rightson(p)].xval);
		tree[p].nval=min(tree[leftson(p)].nval,tree[rightson(p)].nval);
	}
	inline void build(int l,int r,int p){
		tree[p].l=l,tree[p].r=r,tree[p].val=tree[p].tag=0,tree[p].xval=-inf,tree[p].nval=inf;
		if(l==r){
			tree[p].val=tree[p].xval=tree[p].nval=rk[l];
			return ;
		}
		int mid=l+r>>1;
		build(l,mid,leftson(p));
		build(mid+1,r,rightson(p));
		push_up(p);
	}
	inline void spread(int p){
		if(tree[p].tag){
			tree[leftson(p)].val=-tree[leftson(p)].val;
			tree[rightson(p)].val=-tree[rightson(p)].val;
			int lx=tree[leftson(p)].xval,rx=tree[rightson(p)].xval;
			int ln=tree[leftson(p)].nval,rn=tree[rightson(p)].nval;
			tree[leftson(p)].xval=-ln;
			tree[leftson(p)].nval=-lx;
			tree[rightson(p)].xval=-rn;
			tree[rightson(p)].nval=-rx;
			tree[leftson(p)].tag^=1,tree[rightson(p)].tag^=1;
			tree[p].tag=0;
		}
	}
	inline void dupdate(int x,int k,int p){
		if(tree[p].l==tree[p].r){
			tree[p].val=tree[p].xval=tree[p].nval=k;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(x<=mid)dupdate(x,k,leftson(p));
		else dupdate(x,k,rightson(p));
		push_up(p);
	}
	inline void update(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r){
			tree[p].val=-tree[p].val;
			int xx=tree[p].xval,nn=tree[p].nval;
			tree[p].xval=-nn;
			tree[p].nval=-xx;
			tree[p].tag^=1;
			return;
		}
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		if(l<=mid)update(l,r,leftson(p));
		if(r>mid)update(l,r,rightson(p));
		push_up(p);
	}
	inline int query(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].val;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=0;
		if(l<=mid)res+=query(l,r,leftson(p));
		if(r>mid)res+=query(l,r,rightson(p));
		return res;
	}
	inline int xquery(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].xval;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=-inf;
		if(l<=mid)res=max(res,xquery(l,r,leftson(p)));
		if(r>mid)res=max(res,xquery(l,r,rightson(p)));
		return res;
	}
	inline int nquery(int l,int r,int p){
		if(tree[p].l>=l&&tree[p].r<=r)return tree[p].nval;
		spread(p);
		int mid=tree[p].l+tree[p].r>>1;
		int res=inf;
		if(l<=mid)res=min(res,nquery(l,r,leftson(p)));
		if(r>mid)res=min(res,nquery(l,r,rightson(p)));
		return res;
	}
}ST;
struct node2{
	int u,v,w;
}E[MAXN];
namespace HPD{
	inline void getval(int x,int y){
		int res=0;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			res+=ST.query(dfn[top[x]],dfn[x],1);
			x=father[top[x]];
		}
		if(dep[x]!=dep[y]){
			if(dep[x]>dep[y])swap(x,y);
			res+=ST.query(dfn[x]+1,dfn[y],1);
		}
		printf("%d\n",res);
	}
	inline void getmax(int x,int y){
		int res=-inf;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			res=max(res,ST.xquery(dfn[top[x]],dfn[x],1));
			x=father[top[x]];
		}
		if(dep[x]!=dep[y]){
			if(dep[x]>dep[y])swap(x,y);
			res=max(res,ST.xquery(dfn[x]+1,dfn[y],1));
		}
		printf("%d\n",res);
	}
	inline void getmin(int x,int y){
		int res=inf;
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			res=min(res,ST.nquery(dfn[top[x]],dfn[x],1));
			x=father[top[x]];
		}
		if(dep[x]!=dep[y]){
			if(dep[x]>dep[y])swap(x,y);
			res=min(res,ST.nquery(dfn[x]+1,dfn[y],1));
		}
		printf("%d\n",res);
	}
	inline void modify(int x,int y){
		while(top[x]!=top[y]){
			if(dep[top[x]]<dep[top[y]])swap(x,y);
			ST.update(dfn[top[x]],dfn[x],1);
			x=father[top[x]];
		}
		if(dep[x]!=dep[y]){
			if(dep[x]>dep[y])swap(x,y);
			ST.update(dfn[x]+1,dfn[y],1);
		}
	}
	inline void dmodify(int x,int y,int val){
		if(dep[x]>dep[y])swap(x,y);
		ST.dupdate(dfn[y],val,1);
	}
}
int main(){
	scanf("%d",&n);
	for(int i=1,u,v,w;i<n;i++){
		scanf("%d%d%d",&u,&v,&w);
		++u,++v;
		edge[u].push_back({v,w});
		edge[v].push_back({u,w});
		E[i].u=u,E[i].v=v,E[i].w=w;
	}
	dfs1(1,0);
	dfs2(1,1);
	ST.build(1,n,1);
	scanf("%d",&q);
	for(int i=1,x,y;i<=q;i++){
		char opt[10];
		scanf("%s%d%d",opt+1,&x,&y);
		if(opt[1]=='S'){
			++x,++y;
			HPD::getval(x,y);
		}
		else if(opt[1]=='M'&&opt[2]=='A'){
			++x,++y;
			HPD::getmax(x,y);
		}
		else if(opt[1]=='M'&&opt[2]=='I'){
			++x,++y;
			HPD::getmin(x,y);
		}
		else if(opt[1]=='N'){
			++x,++y;
			HPD::modify(x,y);
		}
		else{
			int ux=E[x].u,uy=E[x].v;
			HPD::dmodify(ux,uy,y);
		}
	}
	return 0;
}

大概就是这样，比想象中的简单。