斜率优化dp小结
这个真的好容易啊
个人总结出斜率优化一般步骤:
- 写出 \(\Theta(n^2 )\)的 1d/1d 转移方程:即状态与转移都是一维的方程
- 将dp式化为 \(Y=K*X+B\) 的一次函数形式,尽可能保证斜率 \(K\) ,自变量 \(X\) 的单调性,将本轮答案 \(dp[i]\) 置于由常数和只与 \(i\) 相关变量组成的截距 \(B\) 中。将转移用的 \(dp[j]\) 放置于因变量 \(Y\) 中。
- 通过斜率与自变量的单调性维护凸包。
按照步骤,我们假设 \(j\) 是上一次设置特别行动队的右边界,\(j+1 \sim i\) 为本次特别行动队的区间,由题得方程:
检验正确性后进行如下操作:
- 假设当前的 \(j\) 就是转移的最优解
- 省略极值符号,将转移方程按照上文步骤拆解
- 根据所得方程进行凸包维护
不妨使用前缀和维护士兵的初始战力和
转化为 \(Y=K*X+B\) 的形式:
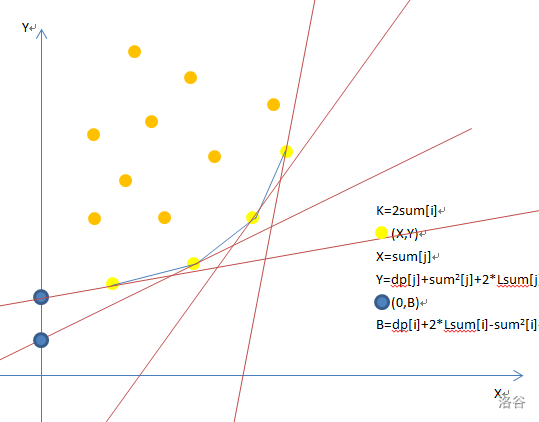
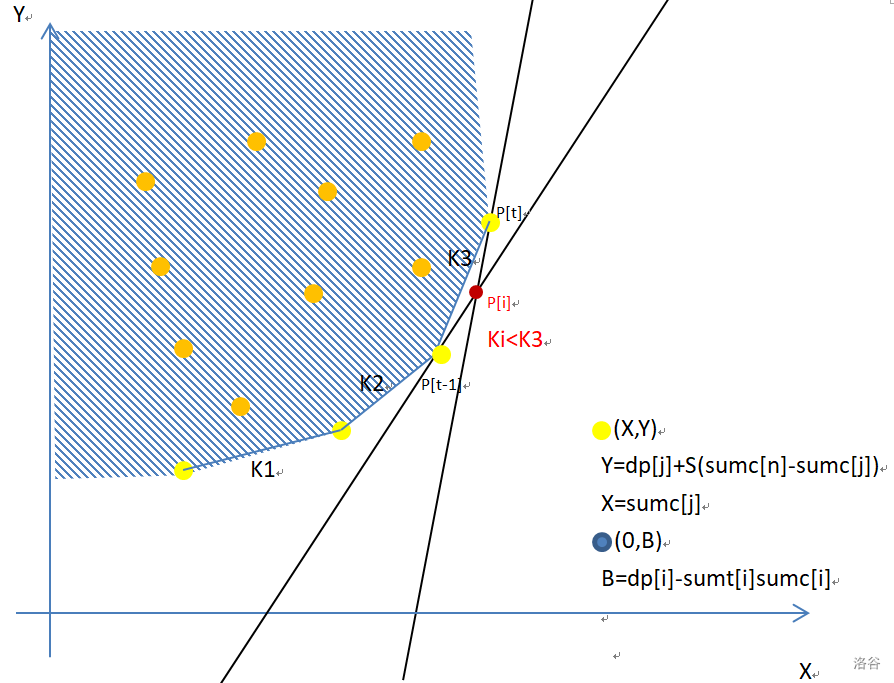
注意到截距 \(B\) 是越大越好的,对于每个固定的 \(j\) ,\(Y\) 是固定的,随着 \(i,j\) 的增长,\(K,X\) 是单调的。于是打开画图:
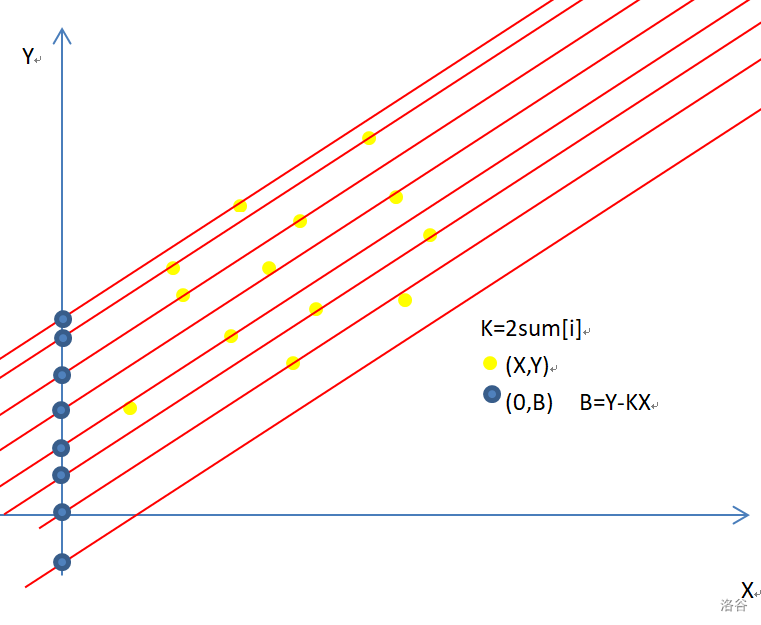
转移 \(dp[i]\) 时考虑扫描每个点
此时斜率固定,图上的黄点所对应的蓝点即截距 \(B\) 的最大值就是我们想要的答案。
因而我们注意到最下面的点不可能成为最优解,然而斜率 \(K\) 是单调递减的,经过反复试验我们得到了不同的 \(K\) 可以取到的答案区间:
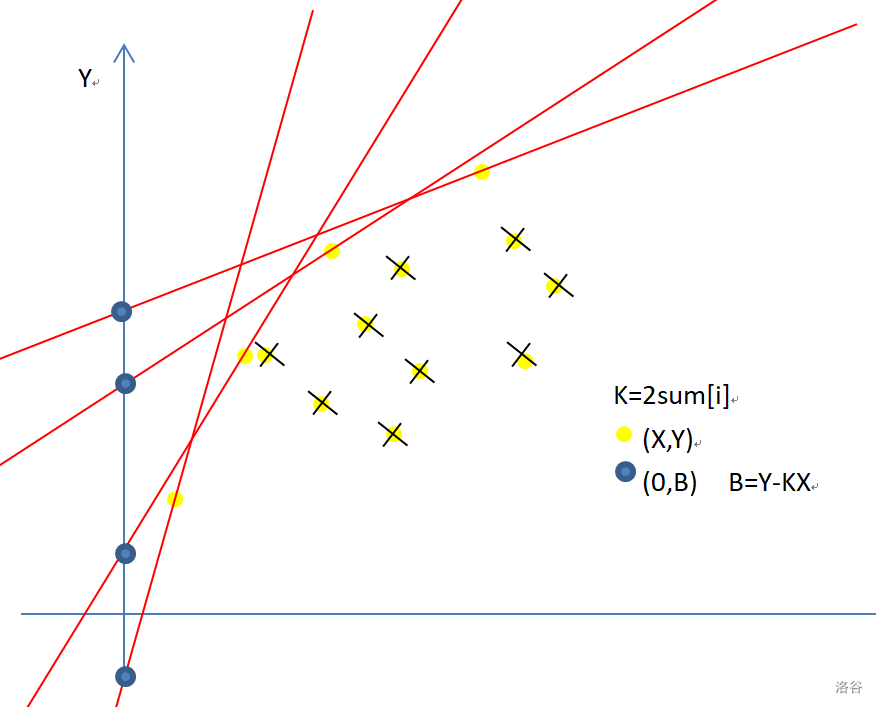
保留的四个点代表了随着斜率的减小而取得的最优解。形成了一个上凸包
考虑如何取舍当前 \(K\) 的答案,连接这个凸包,并计算每一个线段的斜率以及取该点作为答案时的斜率即可发现:
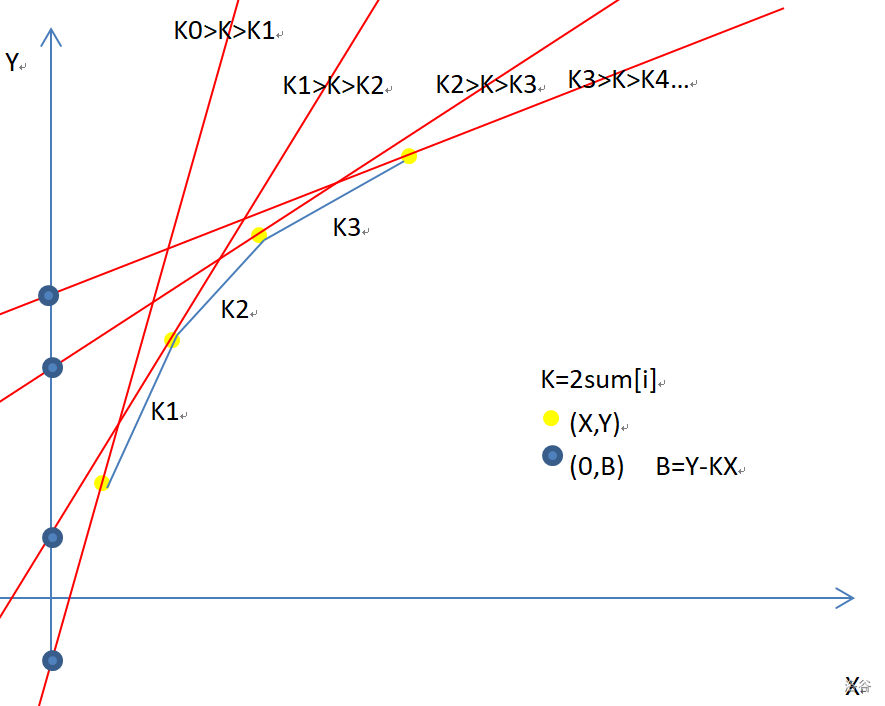
观察得:斜率 \(K\) 的最优黄点是第一对斜率小于 \(K\) 的点对的第一个点
因此我们用单调队列维护斜率,由于当前斜率 \(K\) 的单调性易得:从前不够优秀的黄点以后也不可能成为最优解(*),因此整个转移是线性的,最优决策点 q[H] 一定会递增,这一点很重要,之后会有特殊情况。
通过刚才的斜率比对并修改队头,最优的下标即 \(q[h]\) 。
黄点,也就是当前已有的用来转移的点不是凭空出现的,当前转移的点 \(i\) 也要加入到队列中,并且这一加入可能会导致凸包的破坏:当前的线段比之前的队列中所存储的最不优的最优线段(队尾)更优,当且仅当队尾与 \(i\) 所连的线段的斜率大于队尾线段的斜率。很好理解,斜率尽可能大换来的是该点能解得的截距尽可能大。
翻译成线性规划:
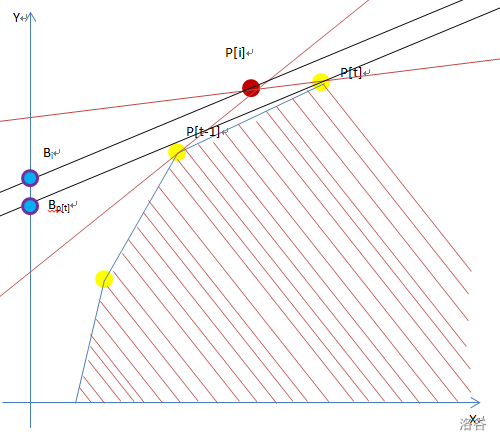
此时 \(q[t]\) 的黄点已经不是最优了,保证斜率单调的情况下弹队尾,让i入队。
#include<bits/stdc++.h>
#define int long long
#define MAXN 1000005
using namespace std;
int n;
struct function{
int a,b,c;
}f;
int sum[MAXN];
int dp[MAXN];
int q[MAXN],h,t;
int Y(int p){//根据上文分析出的X,Y,K等写出对应函数
return dp[p]+f.a*sum[p]*sum[p]-f.b*sum[p];
}
int K(int p){
return 2*f.a*sum[p];
}
double slope(int x1,int x2){
return (Y(x1)-Y(x2))/(sum[x1]-sum[x2])*1.0;
}
signed main(){
scanf("%lld",&n);
scanf("%lld%lld%lld",&f.a,&f.b,&f.c);
for(int i=1;i<=n;i++){
scanf("%lld",&sum[i]);
sum[i]+=sum[i-1];
}
for(int i=1;i<=n;i++){
while(t>h&&slope(q[h],q[h+1])>K(i))++h;//找到第一个斜率小于i对应斜率的线段
dp[i]=dp[q[h]]+f.a*(sum[i]*sum[i]-2*sum[i]*sum[q[h]]+sum[q[h]]*sum[q[h]])+f.b*(sum[i]-sum[q[h]])+f.c;//按照方程转移
while(t>h&&slope(q[t],i)>=slope(q[t],q[t-1]))--t;//将不够优秀的点弹出,点i入队。
q[++t]=i;
}
printf("%lld",dp[n]);
return 0;
}
四张图的K是 \(2*a*sum[i]\) ,wssb。
令 \(dp[i]\) 为装箱到第 \(i\) 个玩具时的最小费用,上一次装箱的右边界为 \(j\) 。
获得了一个癌症级别的多项展开式。
用前缀和替换并移项。
不妨让 \(L\) +=1,重新定义 \(sum[i]\) 为 \(\sum^i_{k=1}{c_k}+i\) ,dp方程得以简化。
然后开始拆解。
转化为 \(Y=K*X+B\) 的形式
其中,\(K\) 与 \(X\) 都单调递增。使用大脑法得出:维护下凸包。
同理,第一个大于第 \(i\) 个点斜率的线段的左端点就是最优解。
线性规划来看,一个点比之前的黄点更优,当且仅当该点在线段下方。
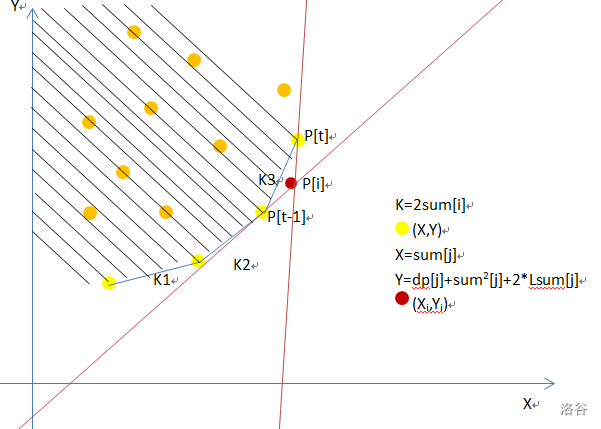
套板子即可。
#include<bits/stdc++.h>
#define int long long
#define MAXN 50005
using namespace std;
int n,l;
int w[MAXN];
int sum[MAXN];
int dp[MAXN];
int q[MAXN],h,t;
int Y(int x){
return dp[x]+sum[x]*sum[x]+2*l*sum[x];
}
int X(int x){
return sum[x];
}
double slope(int x_1,int x_2){
return 1.0*(Y(x_1)-Y(x_2))/(X(x_1)-X(x_2));
}
signed main(){
scanf("%lld%lld",&n,&l);
++l;
for(int i=1;i<=n;i++){
scanf("%lld",&w[i]);
sum[i]=sum[i-1]+w[i]+1;
}
for(int i=1;i<=n;i++){
//dp[i]=min(dp[i],dp[j]+(sum[i]-sum[j]+(i-j-1)-l)*(sum[i]-sum[j]+(i-j-1)-l)); lsum
//dp[i]=dp[j]+(sum[i]-sum[j]-l)(sum[i]-sum[j]-l)
//dp[i]=dp[j]+(sum[i]-sum[j])2+l2-2l(sum[i]-sum[j])
//dp[i]=dp[j]+sum2[i]+sum2[j]-2sum[i]sum[j]+l2-2lsum[i]+2lsum[j]
// Y = k X + B
//dp[j]+sum2[j]+2lsum[j]=2sum[i]sum[j]+dp[i]-sum2[i]+2lsum[i]-l2
while(t>h&&slope(q[h],q[h+1])<=2.0*sum[i])++h;//找最优解
dp[i]=dp[q[h]]+(sum[i]-sum[q[h]]-l)*(sum[i]-sum[q[h]]-l);//转移
while(t>h&&slope(q[t-1],q[t])>=slope(q[t-1],i))--t;//更新答案
q[++t]=i;
}
printf("%lld",dp[n]);
return 0;
}
(*)性质是一个大前提,事实上这个大前提是可以不成立的。
先推 \(\Theta(n^2)\) 方程。
\(num\) 是已分的组数,问题是我们不能使用额外的维度来运行 dp。
把方程拆开,借助题解发现方程的两部分可以分开处理。自 \(i\) 结束的每次分组影响的是 \(i+1\sim n\) 的所有货物的处理时间,进而,\(dp[i]\) 对之后所有分组的代价影响 \(C_{extra}\)表示为:
如果分组左端点下标组成的集合为\(T\),\(S\) 对最终的 \(dp[n]\) 的影响:
脑子不好想不来所以本人还画了一个图:
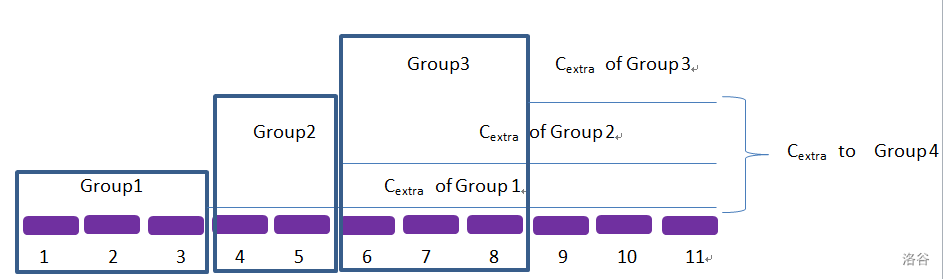
每个分组对总影响各取所需即可。但是我们只需要 \(dp[n]\) 的分组,此时的 \(C_{extra}\) 对其影响如图中 \(Group_4\) 一样,所以 \(dp[n]\) 的额外代价为先前所有额外代价之和,我们在处理 \(dp[i]\) 时顺带计算 \(C_{extra_i}\) 即可。
顺带转化为前缀和形式:
然后按照之前的方法拆解。
尝试进一步分析时发现了问题:\(|T_i|<2^8\) ,即 \(K=sumt[i]\) 不具备单调性。进而对 \(dp[i]\) 转移时的抉择不是线性复杂度。单调队列队头因此始终有利用可能,不得出队。
不过这不影响决策点的位置:第一个斜率大于 \(sumt[i]\) 的线段的左端点。
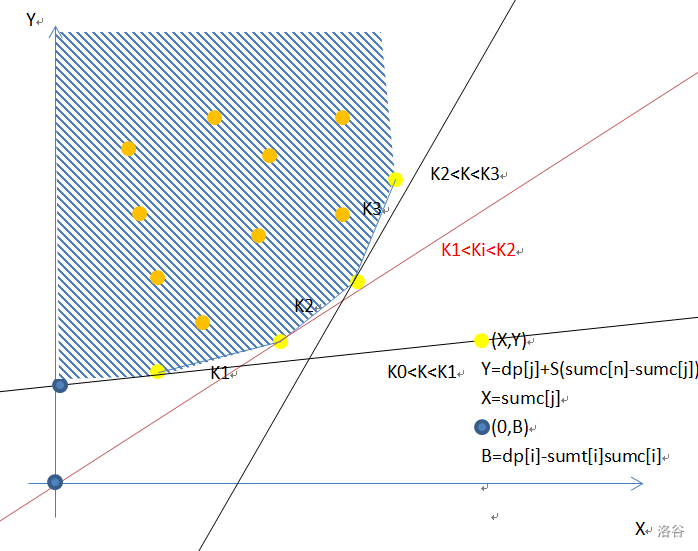
不过此时要用二分查找。
当前点比原先黄点更优,当且仅当其于末位黄点下方。
#include<bits/stdc++.h>
#define int long long
#define MAXN 300005
using namespace std;
int n,s;
struct mission{
int c,t;
}p[MAXN];
int csum[MAXN],tsum[MAXN];
int dp[MAXN];
int q[MAXN],h,t;
int Y(int x){
return dp[x]-s*csum[x];
}
int X(int x){
return csum[x];
}
double slope(int x_1,int x_2){
return 1.0*(Y(x_1)-Y(x_2))/(X(x_1)-X(x_2));
}
int geth(int x){
int l=h,r=t,res=r;//res始终没有更新说明该点的斜率是有史以来最大的,最优解为队尾。
while(l<=r){
int mid=l+r>>1;
if(slope(q[mid+1],q[mid])>=(1.0*tsum[x]))r=mid-1,res=mid;
else l=mid+1;
}
return q[res];
}
signed main(){
scanf("%lld%lld",&n,&s);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&p[i].t,&p[i].c);
tsum[i]=tsum[i-1]+p[i].t;
csum[i]=csum[i-1]+p[i].c;
}
for(int i=1;i<=n;i++){
int loc=geth(i);
dp[i]=dp[loc]+tsum[i]*(csum[i]-csum[loc])+s*(csum[n]-csum[loc]);
while(t>h&&slope(i,q[t-1])<=slope(q[t],q[t-1]))--t;
q[++t]=i;//正常处理
}
printf("%lld",dp[n]);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号