中缀表达式转逆波兰表达式(后缀表达式)
编写程序,将任意一个合法的中缀表达式转换成逆波兰式。
【问题描述】表达式计算是实现程序设计语言的基本问题之一。在计算机中进行算术表达式的计算可通过栈来实现。通常书写的算术表达式由操作数、运算符以及圆括号连接而成。为简便起见,本题只讨论双目运算符。
算术表达式的两种表示如下:
⑴中缀表达式:把双目运算符出现在两个操作数中间的表示,称为算术表达式的中缀表示。中缀表示的算术表达式,称为中缀算术表达式,也称中缀表达式。如表达式2+5*6就是中缀表达式。
⑵后缀表达式:中缀表达式的计算比较复杂。能否把中缀表达式转换成另一种形式的表达式,使计算简单化呢?波兰科学家卢卡谢维奇(Lukasiewicz)提出了算术表达式的另一种表示,即后缀表式,又称逆波兰式。
逆波兰式即是将算术表达式用后缀方法表示,即,把运算符放在两个运算对象的后面。逆波兰式也称后缀算术表达式,或后缀表达式。在逆波兰式中,不存在括号,也不存在优先级的差别,计算过程完全按运算符出现的先后次序进行,整个计算过程仅需一遍扫描便可完成,比中缀表达式的计算简单。
例如,12!4!-!5!/就是一个逆波兰式。其中’!’表示操作数间的空格,因减法运算符在前,除法运算符在后,所以应先做减法,后做除法;减法的两个操作数是它前面的12和4,其中第一个数12是被减数,第二个数4是减数;除法的两个操作数是它前面的12减4的差(即8)和5,其中8是被除数,5是除数。
请查阅中缀表达式转换成对应的后缀算术表达式的规则,完成本题。 表2是一些中缀表达式与后缀表达式对应的例子:
|
表1 中缀表达式与对应的逆波兰式 |
|
|
中缀表达式 |
后缀表达式 |
|
3/5+6 |
3!5!/!6!+ |
|
16-9*(4+3) |
16!9!4!3!+!*!- |
|
2*(x+y)/(1-x) |
2!x!y!+!*!1!x!-!/ |
|
(25+x)*(a*(a+b)+b) |
25!x!+!a!a!b!+!*!b!+!* |
【假设条件】本题应对输入的中缀表达式,输出其对应的逆波兰式。假定表达式一定是合法的,且其中的数字均为1位整数,运算符包括:+,-,*,/,(,)。输入输出均为字符串形式。可以如下形式实现:void InfixToPostfix(char *infix, char *posfix);
数据结构的周作业,应该不会有同学看到这篇文章趴hhh
虽然中缀表达式符合人们的日常习惯,但是在计算机中,为了方便计算表达式的值,一般都是采用前缀表达式或者后缀表达式,所以就需要我们能够将中缀表达式进行相应的转换,另外在题目中已经对后缀表达式进行了详细的阐述,这里不再赘述。
需要提到的是:算术表达式中由三个部分组成,操作数,运算符和圆括号。在中缀表达式中有时括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来,用于指示运算的次序。而在前缀表达式和后缀你表达式中不会存在括号,运算符都按照其优先级进行了相应的排序.
如果不储存最后的后缀表达式,我们在扫描字符串的时候直接将其输出的话,就只需要用到一个栈来储存运算符。
转换的过程如下,慢慢思考的话整个过程还是比较简单的:
1,初始化储存运算符的栈S1
2,从左往右扫描中缀表达式
3,遇到操作数的时候,将其输出
4,遇到运算符的时候,比较其与S1栈顶运算符的优先级
1,如果S1为空,或者栈顶运算符为左括号"(",直接将此运算符入栈
2,否则如果优先级比栈顶运算符高,也将该运算符压入S1,注意没有相等
3,否则将S1栈顶的运算符弹出并输出,再次转到4.1,令运算符与栈顶新的运算符进行比较
5,遇到括号:
1,如果是左括号,直接压入S1
2,如果是右括号,舍弃右括号,并依次弹出S1栈顶的运算符,直到遇到左括号,再将左括号舍弃
6,重复步骤2-->5,直到表达式最右边
7,将S1中剩余的运算符依次弹出并输出,最后显示的就是转换后的逆波兰式(后缀表达式)
接下来是代码实现,按照上面的分析步骤进行代码编写即可:
1,初始化储存运算符的栈S1:
typedef struct{
int top;
char ch[100];
}Stack;
#define LEN sizeof(Stack)
Stack *init(){
Stack* stack=(Stack*)malloc(LEN);
stack->top=0;
return stack;
}
用数组来模拟栈,初始化空间为ch[100],栈顶指针top最开始设置为0
2,从左往右扫描中缀表达式
for(i=0;i<strlen(infix);)
这里的infix数组是输入的中缀表达式字符串,没有设置i++的原因是分情况进行讨论,避免i重复累加
3,遇到操作数的时候,将其输出
if(infix[i]>='0'&&infix[i]<='9'){
while(infix[i]>='0'&&infix[i]<='9'){
printf("%c",infix[i]);
i++;
}
printf("!");
}
我们不再使用另一个队列或数组对其结果进行储存,而是直接将符合的结果直接输出,节省了空间并且简化操作,输出独立的数字之后再输出"!"进行分割
4,遇到运算符的时候,比较其与S1栈顶运算符的优先级
这里与栈顶运算符优先级的比较,为了避免重复写代码,我们将其模块化写成check()函数,传入两个栈顶运算符和当前运算符进行优先级比较。
当前运算符的优先级比栈顶运算符的优先级高的时候,我们就令其入栈,而仔细思考之后只有一种情况,也就是栈顶运算符为"+,-,("的时候,并且当前运算符为"/ *"的时候,才会入栈,其余情况是相等或者低于,就不用入栈,直接弹出栈顶元素,然后用新的栈顶元素继续比较
bool check(char a,char b){
//a为栈顶元素,b为当前元素
//返回true时,将当前元素压入栈中, 即当前运算符比栈顶运算符的优先级高
//返回false时 ,即当前运算符与栈顶运算符的优先级相等或低
if(a=='('){
return true;
}
if((a=='+'||a=='-')&&(b=='*'||b=='/')){
return true;
}else{
return false;
}
}
5,遇到括号:
括号分为左括号和右括号,左括号直接入栈,右括号的话直接抛弃,并且弹出栈中左括号上面的所有运算符,再抛弃左括号
if(infix[i]==')'){
while(stack->ch[stack->top]!='('){
pop(stack);
if(stack->top>0||i<strlen(infix)){
printf("!");
}
}
stack->top--;
i++;
}else if(stack->top==0||infix[i]=='('){
push(stack,infix[i]);
i++;
}
6,重复步骤2-->5,直到表达式最右边
第六步直接在for循环里面完成了,就不用再说
7,将S1中剩余的运算符依次弹出并输出,最后显示的就是转换后的逆波兰式(后缀表达式)
while(stack->top){
pop(stack);
if(stack->top>0||i<strlen(infix)){
printf("!");
}
}
然后是完整代码:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
typedef struct{
int top;
char ch[100];
}Stack;
int flag=1;
#define LEN sizeof(Stack)
Stack *init(){
Stack* stack=(Stack*)malloc(LEN);
stack->top=0;
return stack;
}
void push(Stack* stack,char ch){
stack->top++;
stack->ch[stack->top]=ch;
}
void pop(Stack* stack){
if(stack->top==0){
return;
}
printf("%c",stack->ch[stack->top]);
stack->top--;
}
bool check(char a,char b){
//a为栈顶元素,b为当前元素
//返回true时,将当前元素压入栈中, 即当前运算符比栈顶运算符的优先级高
//返回false时 ,即当前运算符与栈顶运算符的优先级相等或低
if(a=='('){
return true;
}
if((a=='+'||a=='-')&&(b=='*'||b=='/')){
return true;
}else{
return false;
}
}
void InfixToPostfix(char *infix){
Stack *stack=init();
int i;
for(i=0;i<strlen(infix);){
if(infix[i]>='0'&&infix[i]<='9'){
while(infix[i]>='0'&&infix[i]<='9'){
printf("%c",infix[i]);
i++;
}
printf("!");
}
if(infix[i]==')'){
while(stack->ch[stack->top]!='('){
pop(stack);
if(stack->top>0||i<strlen(infix)){
printf("!");
}
}
stack->top--;
i++;
}else if(stack->top==0||infix[i]=='('){
push(stack,infix[i]);
i++;
}else if(check(stack->ch[stack->top],infix[i])){
push(stack,infix[i]);
i++;
}else{
pop(stack);
if(stack->top>0||i<strlen(infix)){
printf("!");
}
}
}
while(stack->top){
pop(stack);
if(stack->top>0||i<strlen(infix)){
printf("!");
}
}
}
int main(){
char infix[100]="3/5+6";
InfixToPostfix(infix);
return 0;
}
主函数里面的infix是我们输入的字符串,当其中缀表达式为:16-9*(4+3) 的时候,输出的结果为:
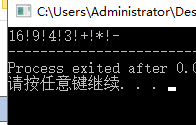
再测试一下题目里面的3/5+6式子,输出结果为:
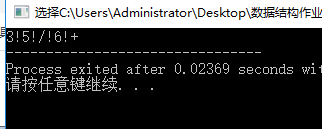
对于这种式子是会失败的:2*(x+y)/(1-x)
从前面的代码也可以看出来,我们判断数字是0--9之间,但是这里是x,y,所以判断不起作用,但是题目里面是:

给出的是一位整数,即合法的式子,我们就能够得到正确的结果,以上
参考博客:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号