字典树(Trie) 与双数组字典树(DoubleArrayTrie) - 学海一扁舟

字典树(Trie) 与双数组字典树(DoubleArrayTrie)

======================= **基础知识** =======================

字典树(Trie): 单词查找树, 可用于单词查找，字符串排序；

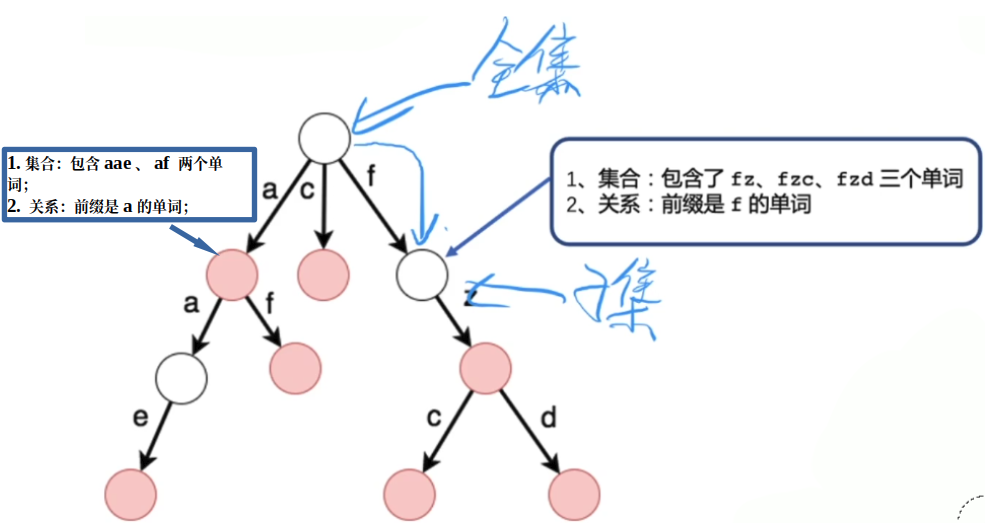
　　在大部分的树中， 节点代表集合；边代表关系；(很重要，代码实现中很多地方都体现）；

　　字典树的具体结构如下图，其中每一条边代表一个字符；不同节点颜色代表以该节点结尾的单词是否存在(粉色：存在；白色：不存在）。

双数组字典树(DoubleArrayTrie)： 逻辑结构还是那个结构，只是换了一种信息表示方法；空间利用率极高，节省空间；

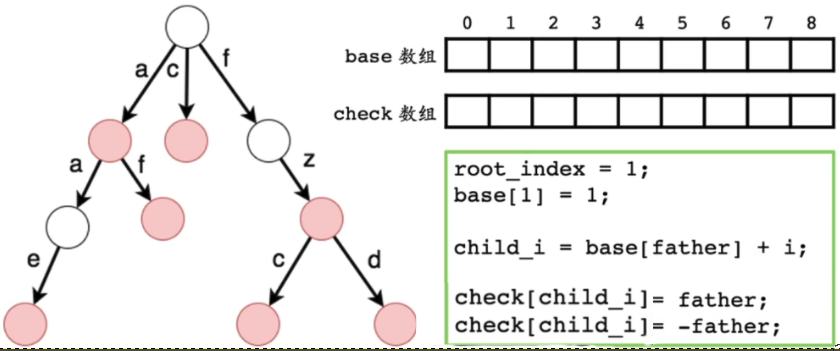
　　　　　　　　　　　　　　　　其中有类似完全二叉树知识点；（父节点与子节点之间关系child_i = base[father] + i);

　　　　　　　　　　　　　　　　也有些理念类似 hashmap ，都会涉及到冲突(check[child_i] = fater)，以及各种解决冲突方式；

　　结构性质：通过2个数组(base, check) 实现字典树的信息记录： base[] 记录每个节点的基数，其对应的所有子节点可以通过 base[father] + i 来找到；而每个父节点并不一定用完26个子节点，所有就会有部分节点信息处于可用状态。所以对于后面节点来讲，可以利用前面父节点没用上的子节点；对于子节点来讲，如果可能由 >1个父节点到达，就通过check[] 标记父节点下标，有因为下标都 >0, 所以用负数表示结尾字符；

　　这里对于父节点基数的选取，来实现所有子节点都只有唯一指向的父节点下标是 DAT 中可以做很多文章的地方；

　　这种做法类似与DP 中两种解题思路（从哪里来；到哪里去）；对于DAT 来讲，通过check 数组记录了每个节点从哪里来；而Trie 与 Updated Trie 都通过记录到从该节点可以到哪里去；这就是对于信息的不同表示方法；

　　优点在空间利用率极高，远比Updated Trie节省空间；

　　　　a. 基础版本Trie：通过在每个节点中Node *next[26] 实现每条边信息记录；每个节点空间为 sizeof(Node);

　　　　b. Updated Trie：通过数组记录下标方式实现 int next[26] 实现每条边的信息记录；(sizeof(int) <= sizeof(Node*));

　　　　c. Double Array Trie：将父节点与子节点之间关系通过类似完全二叉树的方式实现(child_i = base[father] + i)，而不再是通过数组记录方式；通过check[child_i] = father 方式指明父节点，解决冲突问题，通过-father作为字符结尾标记；最好情况下每个节点空间 sizeof(int) * 2，最差情况等价与Updated Trie;

======================= **代码演示** =======================

1. 字典树(Trie) 基本代码：

  1 #include <string>
  2 #include <iostream>
  3 using namespace std;
  4 #define BASE 26
  5 
  6 class Node{
  7 public:
  8     Node():flag(false) {
  9         for(int i = 0; i < BASE; ++i) next[i] = nullptr;
 10     }
 11     ~Node() {}
 12     bool flag;
 13     Node *next[BASE];
 14 };
 15 
 16 class Trie{
 17 public:
 18     Trie() {
 19         root = new Node();
 20     }
 21     ~Trie() {
 22         clearNode(root);
 23     }
 24     bool insert(string s) {
 25         Node *pnode = root;
 26         for(auto &x : s) {
 27             int ind = x - 'a';
 28             if(pnode->next[ind] == nullptr) pnode->next[ind] = new Node();
 29             pnode = pnode->next[ind];
 30         }
 31         if(pnode->flag) return false;
 32         pnode->flag = true;
 33         return true;
 34     }
 35 
 36     bool search(string s) {
 37         Node *pnode = root;
 38         for(auto &x : s) {
 39             int ind = x - 'a';
 40             if(pnode->next[ind] == nullptr) return false;
 41             pnode = pnode->next[ind];
 42         }
 43         return pnode->flag;
 44     }
 45     void output() {
 46         __output(root, "");
 47         return;
 48     }
 49 
 50     Node *root;
 51 
 52 private:
 53     static void clearNode(Node *pnode) {
 54         if(pnode == nullptr) return;
 55         for(int i = 0; i < BASE; ++i) clearNode(pnode->next[i]);
 56         delete pnode;
 57         return;
 58     }
 59 
 60     static void __output(Node *p, string s) {
 61         if(p == nullptr) return;
 62         if(p->flag) printf("%s\n", s.c_str());
 63         for(int i = 0; i < BASE; ++i) {
 64             if(p->next[i]) __output(p->next[i], s+(char(i + 'a')));
 65         }
 66         return;
 67     }
 68 
 69 }; 
 70 
 71 
 72 int main()
 73 {
 74     int n,op;
 75     string input; 
 76     Trie t1;
 77     cin >> n;
 78     while(n--) {
 79         cin >> input;
 80         t1.insert(input);
 81     }
 82 
 83     printf("out put all words in seq:\n");
 84     t1.output();
 85 
 86     while(cin >> input) {
 87         printf("find string: %10s, result is %d\n", input.c_str(), t1.search(input));
 88     }
 89 
 90     return 0;
 91 }
 92 
 93  //input EXAM
 94 7
 95 hello
 96 world
 97 angle
 98 trie
 99 doublearray
100 test
101 check
102 llo
103 trie
104 hel
105 twes
106 angle

Trie

2. 使用数组下标代替指针，减少Trie 占用空间；其中index = 0 为特殊位，index = 1 为根节点；

 1 #include <string>
 2 #include <iostream>
 3 using namespace std;
 4 
 5 #define BASE 26
 6 #define MAX_CNT 10000
 7 class Node {
 8 public:
 9     bool flag;
10     int next[BASE];
11     void clear(){
12         flag = 0;
13         for(int i = 0; i < BASE; ++i) next[i] = 0;
14         return;
15     }
16 }Trie[MAX_CNT];
17 
18 int root, cnt;
19 void clearTrie() {          //通过函数实现初始化
20     root = 1,cnt = 2;       //index = 0: 作为空值； index = 1 ： 作为根； cnt = 2: 取决于下面NewNode实现；
21     Trie[root].clear();
22     return;
23 }
24 
25 int getNewNode(){
26     Trie[cnt].clear();
27     return cnt++;
28 }
29 
30 void insert(string s) {
31     int p = root;
32     for(auto x : s) {
33         int ind = x - 'a';
34         if(Trie[p].next[ind] == 0) Trie[p].next[ind] = getNewNode();
35         p = Trie[p].next[ind];
36     }
37     Trie[p].flag = true;
38     return;
39 }
40 
41 bool search(string s) {
42     int p = root;
43     for(auto x : s) {
44         int ind = x - 'a';
45         p = Trie[p].next[ind];
46         if(p == 0) return false;
47     }
48     return Trie[p].flag;
49 }
50 
51 void __output(int idx, string s) {
52     if(idx == 0) return;
53     if(Trie[idx].flag) printf("%s\n", s.c_str());
54     for(int i = 0; i < BASE; ++i) {
55         if(Trie[idx].next[i] == 0) continue;
56         __output(Trie[idx].next[i], s + char(i + 'a'));
57     }
58     return;
59 }
60 
61 void output() {
62     __output(root, "");
63     return;
64 }
65 
66 int main()
67 {
68     int n;
69     string input; 
70     clearTrie();
71     cin >> n;
72     while(n--) {
73         cin >> input;
74         insert(input);
75     }
76 
77     printf("out put all words in seq:\n");
78     output();
79 
80     while(cin >> input) {
81         printf("find string: %10s, result is %d\n", input.c_str(), search(input));
82     }
83 
84     return 0;
85 }

Updated_Trie

3.双数组字典树(Double Array Trie): 使用2个数组以及类似完全二叉树父/子映射方式，记录树的一层层关系；；独立成词通过负数实现；

　　下面代码实现中：对于check 数组中冲突问题，使用最简单的不断查找方式实现；

  1 #include <iostream>
  2 #include <cstring>
  3 using namespace std;
  4 #define BASE 26
  5 #define TEST_SEARCH(func, input) printf("%15s return %d\n", #func, func(input))
  6 //Default Trie
  7 struct Node {
  8     bool flag;
  9     Node *next[BASE];
 10     Node():flag(false){
 11         for(int i = 0; i < BASE; ++i) next[i] = nullptr;
 12     }
 13 };
 14 int cnt = 1;
 15 Node *root;
 16 
 17 void insert(string s) {
 18     Node *p = root;
 19     for(int i = 0; s[i]; ++i) {
 20         int idx = s[i] - 'a';
 21         if(p->next[idx] == nullptr) {
 22             p->next[idx] = new Node();
 23             cnt++;
 24         }
 25         p = p->next[idx];
 26     }
 27     p->flag = true;
 28     return;
 29 }
 30 
 31 bool search(string s) {
 32     Node *p = root;
 33     for(int i = 0; s[i]; ++i) {
 34         int ind = s[i] - 'a';
 35         if(p->next[ind] == nullptr) return false;
 36         p = p->next[ind];
 37     }
 38     return p->flag;
 39 }
 40 
 41 void __output(Node *p, string s) {
 42     if(p->flag) cout << s << endl;
 43     for(int i = 0; i < BASE; ++i) {
 44         if(nullptr == p->next[i])  continue;
 45         __output(p->next[i], s + char(i + 'a'));
 46     }
 47     return;
 48 }
 49 
 50 void output(){
 51     __output(root, "");
 52     return;
 53 }
 54 
 55 //Updated Trie;
 56 #define MAX_N 1000
 57 struct Node_updated{
 58     bool flag;
 59     int next[BASE];
 60 }Trie[MAX_N];
 61 
 62 int root_updated, cnt_updated;
 63 void clearTrie() {          //通过函数实现初始化
 64     root_updated = 1, cnt_updated = 2;      //index = 0: 作为空值； index = 1 ： 作为根； cnt_updated = 2:
 65     Trie[root_updated].flag = false;
 66     for(int i = 0; i < BASE; ++i) Trie[root_updated].next[i] = 0;
 67     return;
 68 }
 69 
 70 int genNewNode(){
 71     Trie[cnt_updated].flag = false;
 72     for(int i = 0; i < BASE; ++i) Trie[cnt_updated].next[i] = 0;
 73     return cnt_updated;
 74 }
 75 
 76 void insert_updated(string s) {
 77     int cur = root_updated;
 78     for(int i = 0; s[i]; ++i) {
 79         int index = s[i] - 'a';
 80         if(0 == Trie[cur].next[index]) {
 81             Trie[cur].next[index] = genNewNode();
 82             cnt_updated++;
 83         }
 84         cur = Trie[cur].next[index];
 85     }
 86     Trie[cur].flag = true;
 87     return;
 88 }
 89 
 90 bool search_updated(string s) {
 91     int cur = root_updated;
 92     for(int i = 0; s[i]; ++i) {
 93         int index = s[i] - 'a';
 94         if(0 == Trie[cur].next[index]) return false;
 95         cur = Trie[cur].next[index];
 96     }
 97     return Trie[cur].flag;
 98 }
 99 
100 void __output(int idx, string s) {
101     if(Trie[idx].flag) printf("%s\n", s.c_str());
102     for(int i = 0; i < BASE; ++i) {
103         if(0 == Trie[idx].next[i]) continue;
104         __output(Trie[idx].next[i], s + char(i + 'a'));
105     }
106     return;
107 }
108 
109 void output_updated() {
110     __output(root_updated, "");
111     return;
112 }
113 
114 
115 //DOUBLE ARRAY TRIE
116 int *base, *check, root_DAT, cnt_DAT;
117 int getBase(int r, int *base, int *check) {
118     int b = 1, flag = 0;
119     while(0 == flag) {
120         b++;
121         flag = 1;
122         for(int i = 0; i < BASE; ++i) {
123             if(0 == Trie[r].next[i]) continue;
124             if(0 == check[b + i]) continue;  //不用base 数组，因为base 用来指向子节点，而叶子节点没有子节点,
125                                             //                  而check 指向父节点，每个节点都有父节点（除了根,不过根 = 1,不可能到达);
126             flag = 0;
127             break;
128         }
129     }
130     return b;
131 }
132 
133 void convertToDoubleArrayTrie(int r, int d_r, int *base, int *check) {
134     if(r == 0) return;
135     base[d_r] = getBase(r, base, check);
136     for(int i = 0; i < BASE; ++i) {
137         if(0 == Trie[r].next[i]) continue;
138         check[base[d_r] + i] = d_r;
139         if(Trie[Trie[r].next[i]].flag) check[base[d_r] + i] = -d_r;
140     }
141     cnt_DAT = max(cnt_DAT, d_r);
142     for(int i = 0; i < BASE; ++i) {
143         if(0 == Trie[r].next[i]) continue;
144         convertToDoubleArrayTrie(Trie[r].next[i], base[d_r] + i, base, check);
145         cnt_DAT = max(cnt_DAT, base[d_r] + i);
146     }
147 
148     return;
149 }
150 
151 bool search_DAT(string s) {
152     int r = root_DAT;
153     for(int i = 0; s[i]; ++i) {
154         int idx = s[i] - 'a';
155         if(abs(check[base[r] + idx]) != r) return false;
156         r = base[r] + idx;
157     }
158     return check[r] < 0;
159 }
160 
161 
162 
163 int main()
164 {
165     //Default Trie
166     root = new Node();
167     cnt = 1;
168     //Updated Trie
169     clearTrie();
170 
171     int n;
172     string input;
173     cin >> n;
174     while(n--){
175         cin >> input;
176         insert(input);
177         insert_updated(input);
178     }
179 
180     printf("--------------Output all--------------\n");
181     output();
182 #ifdef DEBUG
183     output_updated();
184 #endif
185     printf("----------Done-------------------\n");
186 
187     //Double Array Trie
188     base = (int *)malloc(sizeof(int) * MAX_N);
189     check = (int *)malloc(sizeof(int) * MAX_N);
190     memset(base, 0, sizeof(int) * MAX_N);
191     memset(check, 0, sizeof(int) * MAX_N);
192     root_DAT = 1, cnt_DAT = 1;
193     convertToDoubleArrayTrie(root_updated, root_DAT, base, check);
194 
195 #ifdef DEBUG
196     printf("%6s:","index");
197     for(int i = 0; i < cnt_DAT; ++i) {
198         printf("%3d,",i);
199     }
200     printf("\n%6s:","base");
201     for(int i = 0; i < cnt_DAT; ++i) {
202         printf("%3d,",base[i]);
203     }
204     printf("\n%6s:","check");
205     for(int i = 0; i < cnt_DAT; ++i) {
206         printf("%3d,",check[i]);
207     }
208     printf("\n");
209 #endif
210 
211     printf("%s:\n%25s:%lu\n%25s:%lu\n%25s:%lu\n","memory usage check",
212                 "default Trie size", sizeof(Node) * cnt,
213                 "Updated Trie size", sizeof(Node_updated) * cnt_updated,
214                 "Double Array Trie size", sizeof(int) * 2 * (cnt_DAT + 1));
215     printf("----------------------------------------\n");
216     while(cin >> input) {
217         printf("search word: %s\n", input.c_str());
218         TEST_SEARCH(search, input);
219         TEST_SEARCH(search_updated, input);
220         TEST_SEARCH(search_DAT, input);
221     }
222     return 0;
223 }

DoubleArrayTrie

======================= **经典问题** =======================

1. 208. 实现 Trie (前缀树) :Trie 裸题；

 1 class Trie {
 2 public:
 3 #define BASE 26
 4     struct Node{
 5         bool flag;
 6         int next[BASE];
 7         Node():flag(false) {
 8             for(int i = 0; i < BASE; ++i) next[i] = 0;
 9         }
10     };
11 
12     vector<Node> inform;
13     Trie():inform(vector<Node>(2,Node())) {}
14     
15     void insert(string word) {
16         int r = 1;
17         for(int i = 0; word[i]; ++i) {
18             int index = word[i] - 'a';
19             if(0 == inform[r].next[index]) {
20                 inform[r].next[index] = inform.size();
21                 inform.push_back(Node());
22             }
23             r = inform[r].next[index];
24         }
25         inform[r].flag = true;
26         return;
27     }
28     
29     bool search(string word) {
30         int r = 1;
31         for(int i = 0; word[i]; ++i) {
32             int index = word[i] - 'a';
33             if(0 == inform[r].next[index]) return false;
34             r = inform[r].next[index];
35         }
36         return  inform[r].flag;
37     }
38     
39     bool startsWith(string prefix) {
40         int r = 1;
41         for(int i = 0; prefix[i]; ++i) {
42             int index = prefix[i] - 'a';
43             if(0 == inform[r].next[index]) return false;
44             r = inform[r].next[index];
45         }
46         return true;
47     }
48 };
49 
50 /**
51  * Your Trie object will be instantiated and called as such:
52  * Trie* obj = new Trie();
53  * obj->insert(word);
54  * bool param_2 = obj->search(word);
55  * bool param_3 = obj->startsWith(prefix);
56  */

UpdatedTrie

2. 1268. 搜索推荐系统 : Trie + 记忆化 + 函数封装；

　　这题是字符补全的程序实现，Trie 在实际应用中根据具体需求来实现，所以并没有固定的接口与形式；

  1 class Solution {
  2 public:
  3 #define BASE 26
  4     class Node{
  5         public:
  6             Node():flag(false){
  7                 for(int i = 0; i < BASE; ++i) next[i] = nullptr;
  8             }
  9             bool flag;
 10             Node *next[BASE];
 11     };
 12     Node *root;
 13     void dfs(Node *r, string s, vector<string> &ans) {
 14         if(3 == ans.size()) return;
 15         if(!r) return;
 16         if(r->flag) ans.push_back(s);
 17         for(int i = 0; i < BASE; ++i) {
 18             if(!r->next[i]) continue;
 19             dfs(r->next[i], s + char('a' + i), ans);
 20         }
 21         return;
 22     }
 23 
 24     vector<vector<string>> suggestedProducts(vector<string>& products, string searchWord) {
 25         root = new Node();
 26         for(auto &x : products) {
 27             Node *r = root;
 28             for(int i = 0; x[i]; ++i){
 29                 int index = x[i] - 'a';
 30                 if(!r->next[index]) r->next[index] = new Node();
 31                 r = r->next[index];
 32             }
 33             r->flag = true;
 34         }
 35 
 36         vector<vector<string>> ans;
 37         Node *r = root;
 38         string s = "";
 39         for(auto &c : searchWord) {
 40             s += c;
 41             int index = c - 'a';
 42             vector<string> ret;
 43             if(r) {
 44                 dfs(r->next[index], s, ret);
 45                 r = r->next[index];
 46             }
 47             ans.push_back(ret);
 48         }
 49         return ans;
 50     }
 51 };
 52 
 53 //Updted Trie + 数组记忆化，空间换时间
 54 class Solution {
 55 #define MAX_N 20000
 56 #define BASE 26
 57 struct Trie{
 58     Trie():flag(false) {
 59         for(int i = 0; i < BASE; ++i) next[i] = 0;
 60         p_recomd = new set<string>();
 61     }
 62     bool flag;
 63     int next[BASE];
 64     set<string> *p_recomd;
 65 }trie[MAX_N];
 66 
 67 int root = 1;
 68 int next = 2;
 69 
 70 void insert(string s) {
 71     int p = root;
 72     for(auto x : s) {
 73         int ind = x - 'a';
 74         if(!trie[p].next[ind]) trie[p].next[ind] = next++;
 75         p = trie[p].next[ind];
 76         trie[p].p_recomd->insert(s);
 77         if((trie[p].p_recomd)->size() > 3) (trie[p].p_recomd)->erase(--((trie[p].p_recomd)->end()));
 78     }
 79     trie[p].flag = true;
 80     return;
 81 }
 82 
 83 vector<vector<string>> search(string s) {
 84     int p = root;
 85     vector<vector<string>> ret;
 86     for(auto x : s) {
 87         int ind = x - 'a';
 88         p = trie[p].next[ind];
 89         ret.push_back(vector<string>((trie[p].p_recomd)->begin(), (trie[p].p_recomd)->end()));
 90     }
 91     return ret;
 92 }
 93 
 94 
 95 public:
 96     vector<vector<string>> suggestedProducts(vector<string>& products, string searchWord) {
 97         for(auto x : products) insert(x);
 98         return search(searchWord);
 99     }
100 };

Trie+记忆化

3. 剑指 Offer II 067. 最大的异或 : 应用Trie 性质查找特定要求值；

 1 class Solution {
 2 public:
 3     struct Node {
 4         Node *next[2];
 5         Node(){
 6             for(int i = 0; i < 2; ++i) next[i] = nullptr;
 7         }
 8     };
 9 
10     Node *root;
11     void genTrie(vector<int>& nums) {
12         root = new Node(); 
13         for(auto x : nums) { //必须从高位往低位，优先保证满足高位；另外需要保证每位比较时候对齐,所以每个数字必须相同位数表示；
14             Node *r = root;
15             int loop = 31;
16             while(loop--){
17                 int idx = ((x >> loop) & 1);
18                 if(!r->next[idx]) r->next[idx] = new Node();
19                 r = r->next[idx];
20             }
21         }
22     }
23 
24     int search(int num) {
25         Node *r = root;
26         int loop = 31, ans = 0;
27         while(loop--) {
28             int idx = !((num >> loop) & 1);
29             if(r->next[idx]) {
30                 ans |= (1 << loop);
31                 r = r->next[idx];
32             }else {
33                 r = r->next[!idx];
34             }
35         }
36         return ans;
37     }
38 
39 
40     int findMaximumXOR(vector<int>& nums) {
41         int ans = 0;
42         genTrie(nums);
43         for(auto &x : nums) ans = max(ans, search(x));
44         return ans;
45     }
46 };

应用Trie数据结构查找特定数值

4. 440. 字典序的第K小数字：对于字典树的排序功能的应用；因为数值是指定所有数值，所以Trie 建立会浪费更多时间；

难点在与：对Trie 观察规律，从而避免建立Trie;

 1 class Solution {
 2 public:
 3 #define BASE 10
 4     struct Node{
 5         int cnt;
 6         Node *next[BASE];
 7         Node():cnt(0){
 8             for(int i = 0; i < BASE; i++) next[i] = nullptr;
 9         }
10     };
11     Node *root;
12     void insert(int n) {
13         Node *p = root;
14         vector<int> val;
15         while(n){
16             val.push_back(n % 10);
17             n /= 10;
18         }
19         n = val.size();
20         while(n--) {
21             if(nullptr == p->next[val[n]]) p->next[val[n]] = new Node();
22             p = p->next[val[n]];
23             p->cnt += 1;
24         }
25         return;
26     }
27 
28     int search(Node *p, int k, int val) {
29         if(k == 0) return val;
30         for(int i = 0; i < BASE; ++i) {
31             if(nullptr == p->next[i]) continue;
32             if(p->next[i]->cnt < k) {
33                 k -= p->next[i]->cnt;
34                 continue;
35             }
36             val = val * 10 + i;
37             return search(p->next[i], k - 1, val);
38         }
39         return -1;
40     }
41     
42     int getNodeCnt(long long n, long long cur) {
43         long long next = cur + 1, ret = 0;  //next：定义了在当前层数中，当前分支后的一个分支在当前层的第一个值；
44         n+= 1;
45         //cur: 定义了当前边在树中第几层；然后一层层树往下计算;
46         while(cur <= n) {
47             //通过后一个分支在当前层的第一位 与 当前分支的第一位之间差，求得当前层的个数
48             ret += (min(next, n) - cur);  //防止下一分支的值next已经超出上限 n ;
49             //进入下一层
50             cur *= 10;
51             next *= 10;
52         }
53         return ret;
54     }
55 
56     int search(int n, int k) {
57         int cur = 1;
58         while(k) {
59             int total_cnt = getNodeCnt(n, cur);
60             if(k > total_cnt) {
61                 k -= total_cnt;
62                 cur++;
63             } else {
64                 k -= 1;
65                 if(k) cur *= 10;
66             }
67         }
68         return cur;
69     }
70 
71     int findKthNumber(int n, int k) {
72 //将所有的数值建立Trie, 并记录每个节点值
73 //        root = new Node();
74 //        for(int i = 1; i <= n; ++i) insert(i);
75 //        return search(root, k, 0);
76         return search(n, k);  //两种search 思想是一致的，一条边判断是否满足k 要求，不满足下一条边；
77     }
78 };

Trie排序的应用

5. 676. 实现一个魔法字典： Trie 中search 实现有且只有一个字符不匹配；

　　tips: 1. 提前判断一个不存在条件(if)，在这题中时间差很大； 2. 任何一个循环都可以写成递归；

 1 class MagicDictionary {
 2 public:
 3 #define MAX_N 10000
 4 #define BASE 26
 5     struct Node {
 6         bool flag;
 7         int next[BASE];
 8         Node(): flag(false){
 9             for(int i = 0; i < BASE; ++i) next[i] = 0;
10         }
11     }Trie[MAX_N];
12     int root, cnt, error;
13     MagicDictionary() {
14         root = 1, cnt = 2;
15         error = 0;
16     }
17     
18     void buildDict(vector<string> dictionary) {
19         for(auto &x : dictionary) {
20             int p = root;
21             for(int i = 0; x[i]; ++i) {
22                 int index = x[i] - 'a';
23                 if(!Trie[p].next[index]) Trie[p].next[index] = cnt++;
24                 p = Trie[p].next[index];
25             }
26             Trie[p].flag = true;
27         }
28         return;
29     }
30    
31     bool __search(string s, int i, int p){
32         //if(!p) return false;  //没有提前判断 Trie[p].next[j], 时间差别很大!!
33         for(; s[i]; ++i){
34             int index = s[i] - 'a';
35             if(!Trie[p].next[index]) return false;
36             p = Trie[p].next[index];
37         }
38         return Trie[p].flag;
39     }
40 
41     bool search(string searchWord) {
42         int p = root;
43         for(int i = 0; searchWord[i]; ++i) {
44             int index = searchWord[i] - 'a';
45             for(int j = 0; j < BASE; ++j) {
46                 //if(j == index) continue;    //没有提前判断 Trie[p].next[j], 时间差别很大!!
47                 if(j == index || Trie[p].next[j] == 0) continue;   
48                 if(__search(searchWord, i + 1, Trie[p].next[j])) return true;
49             }
50             if(!Trie[p].next[index]) return false;
51             p = Trie[p].next[index];
52         }
53         return false;
54     }
55 };
56 
57 /**
58  * Your MagicDictionary object will be instantiated and called as such:
59  * MagicDictionary* obj = new MagicDictionary();
60  * obj->buildDict(dictionary);
61  * bool param_2 = obj->search(searchWord);
62  */

Trie中search 方法升级

6 面试题 17.17. 多次搜索 : 字符串查找应用；

  1 //Trie
  2 class Solution {
  3 public:
  4 #define BASE 26
  5 #define MAX_N 100000
  6     struct Node {
  7         int pos;
  8         int next[BASE];
  9         Node() : pos(-1) {
 10             for(int i = 0; i < BASE; ++i) next[i] = 0;
 11         }
 12     }Trie[MAX_N];
 13     int root, cnt;
 14 
 15     void buildTrie(string s, int num) {
 16         int p = root;
 17         for(int idx = 0; s[idx]; ++idx) {
 18             int index = s[idx] - 'a';
 19             if(!Trie[p].next[index]) Trie[p].next[index] = cnt++;
 20             p = Trie[p].next[index];
 21         }
 22         Trie[p].pos = num;
 23         return;
 24     }
 25 
 26     vector<int> search(string s, int i) {
 27         int p = root;
 28         vector<int> ret;
 29         for(; s[i]; ++i) {
 30             int index = s[i] - 'a';
 31             if(!Trie[p].next[index]) return ret; 
 32             p = Trie[p].next[index];
 33             if(Trie[p].pos != -1) ret.push_back(Trie[p].pos);
 34         }
 35         return ret;
 36     }
 37 
 38     vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
 39         root = 1, cnt = 2;
 40         for(int i = 0, I = smalls.size(); i < I; ++i) buildTrie(smalls[i], i);
 41 
 42         vector<vector<int>> ans(smalls.size(), vector<int>());
 43         for(int i = 0; big[i]; ++i){
 44             vector<int> temp = search(big, i);
 45             for(auto &x : temp) ans[x].push_back(i);
 46         }
 47         return ans;
 48     }
 49 };
 50 
 51 //KMP / SUNDAY
 52 class Solution {
 53 public:
 54     //KMP : 
 55     vector<int> KMP(string src, string pat) {
 56         int len_p = pat.size();
 57         if(!len_p) return vector<int>();
 58         vector<int> pre(len_p, -1), ret;
 59         for(int i = 1, j = -1; i < len_p; ++i) {
 60             while(j != -1 && pat[j + 1] != pat[i]) j = pre[j];
 61             if(pat[j + 1] == pat[i]) j += 1;
 62             pre[i] = j;
 63         }
 64 
 65         for(int i = 0, j = -1; i < src.size(); ++i) {
 66             while(j != -1 && src[i] != pat[j + 1]) j = pre[j];
 67             if(src[i] == pat[j + 1]) j += 1;
 68             if(j == len_p - 1) {
 69                 ret.push_back(i - j);
 70                 j = pre[j];
 71             }
 72         }
 73         return ret;
 74     }
 75     
 76     //Sunday:
 77     vector<int> Sunday(string& src, string& pat) {
 78         int len_p = pat.size(), len_s = src.size();
 79         if(!len_p) return vector<int>();
 80 #define BASE 128
 81         vector<int> last(BASE, -1), ret;
 82         for(int i = 0; i < len_p; ++i) last[(pat[i])] = i;
 83         for(int i = 0, I = len_s - len_p; i <= I; i += (len_p - last[(src[i + len_p])])) {
 84             int j = 0;
 85             while(j < len_p && src[i + j] == pat[j]) j += 1;
 86             if(j == len_p) ret.push_back(i);
 87         }
 88 #undef BASE
 89         return ret;
 90     }
 91 
 92     //Shift-And: 这个长度1000，比较麻烦
 93     vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
 94         vector<vector<int>> ret;
 95         for(auto x : smalls) {
 96 //            ret.push_back(KMP(big, x));
 97             ret.push_back(Sunday(big, x));
 98         }
 99         return ret;
100     }
101 };

Trie/KMP/SUNDAY

======================= **应用场景** =======================

Trie最典型的应用：Trie 的具体实现根据不同应用场景不同而不同，所以没有固定的接口或形式；

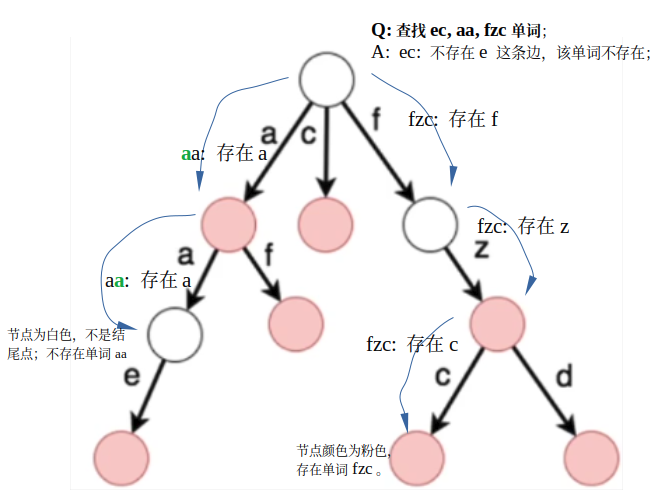
　　　　单词查找：判断是否存在边，以及是否结束节点是否存在单词；

　　　　字符串排序：1）建立字典树；2）DFS该字典树，输出单词，即可实现字符串排序；O(n)

　　　　还可以用于字符补全，拼写检查；

Double Array Trie：

　　1.字符串预处理后需要空间小，节省内存；

　　2. 将所有字符数组序列化到文件中，方便传输到其他电脑/手机；也就意味着可以将字符串处理过程放在服务器端，然后将处理好的这个很小的文件传输到用户终端，方便用户快速检索；

posted on 2022-04-28 23:42 学海一扁舟阅读(625) 评论(0) 编辑收藏举报

刷新页面返回顶部