经典字符串匹配算法

======================= **基础知识** =======================

前置知识：

　　母串S/文本串：被查找源字符串；

　　模式串T：　　 目标字符串；

　　单模匹配问题：只有一个模式串问题；

　　

　　字符串匹配算法需要极强观察能力；

 

常见的算法：

1. 暴力匹配(brute force)：保证不重不漏的进行每一次匹配，实现查找的目的；O(n * m)；

 

2. KMP算法 :  模式串T 匹配 母串S 问题 ==>模式串 匹配 模式串过程; 在处理与匹配过程中，都是寻找到重复部分，减少重复过程；

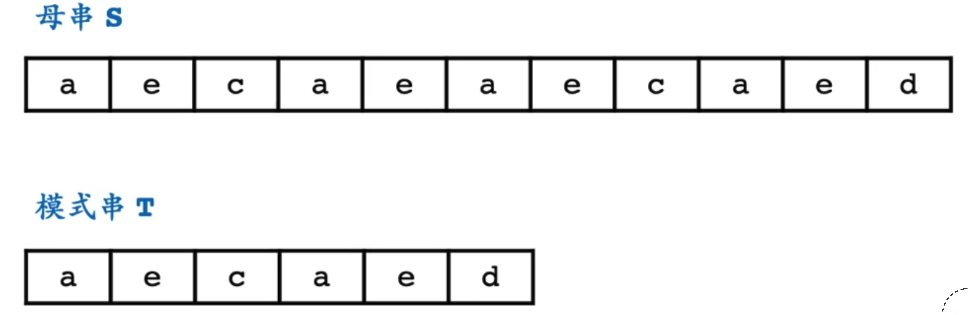
　　针对已经匹配好的部分在母串与模式串一致特性，后移模式串的失配位置前一位在模式串中匹配位置，减少重复匹配过程，继续匹配母串中失配位置，直到找到一个匹配，然后后移母串匹配位i = i + 1;

　

　　但是后移一位，明显并不能匹配；换个说法如果想要后移一位后，母串(a) 失配位置继续能够匹配，那么右边红色阴影部分必须匹配；

　　那么如何实现红色阴影部分的匹配？ 首先母串中红色阴影部分是已经与模式串匹配成功的部分，也就意味着这部分在模式串中有一模一样的(也就是模式串中绿色部分）；

　　那上面问题就变成了，在模式串绿色部分找到模式串失配位置前一位(e)，在模式串中的最长匹配位置(保证不漏)；将模式串移动至该位置，就可以继续匹配母串(a)；这里就变成了模式串 匹配 模式串问题；而模式串的数据是可以预处理的，找出其中的关键信息；

　　关于上面所说的最长匹配位置，因为上面红色阴影部分为了保证不漏，要保证最长匹配；也就是说，假设绿色匹配部分的长度为n(0 ~ (n - 1), 示例中为5)，那么先要看模式串中从头长度为(n - 1) (idx = 0 ~ (n - 2), (前缀)) 是否与 失配位置往前长度为(n - 1) (idx = 1 ~ (n - 1), (后缀)) 匹配； 如果不匹配，那么下一个长度为 n - 2 的前缀 与 后缀 之间是否匹配... ;从而保证不漏；

　　　　

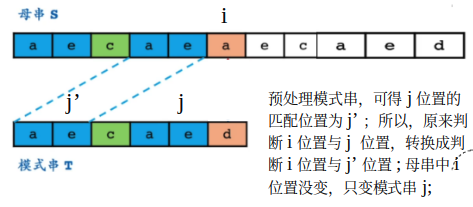
　　对上面过程总结，如果对模式串进行预处理，找到其中每个字符在模式串中匹配位置(Ta = Tb)；当位置i 与 j 发生失配时( j之前是匹配好的数据部分），就将模式串后移(Ta与 Sb 重合), 将 i 与 j' 比较；不断重复这个过程，直到在模式串中找到匹配 i 位置（可以在模式串-1位置设立万能匹配位，保证一定能找到匹配）；然后将i = i + 1 继续匹配；

 

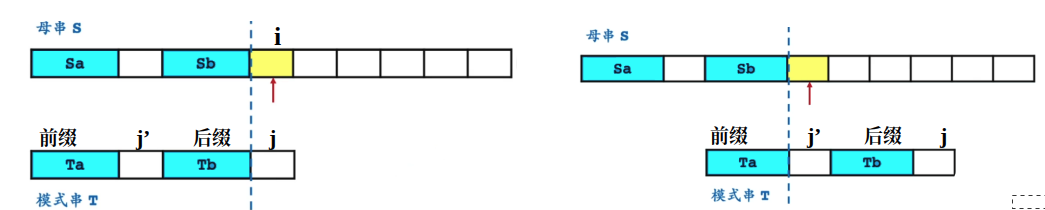
3. Sunday:通过黄金对齐点位，保证不重不漏，同时减少不必要的位置匹配；

 

　　其中对模式串的黄金点位求取过程，必须要保证是该字符在模式串中的最后一位；保证不漏；

 

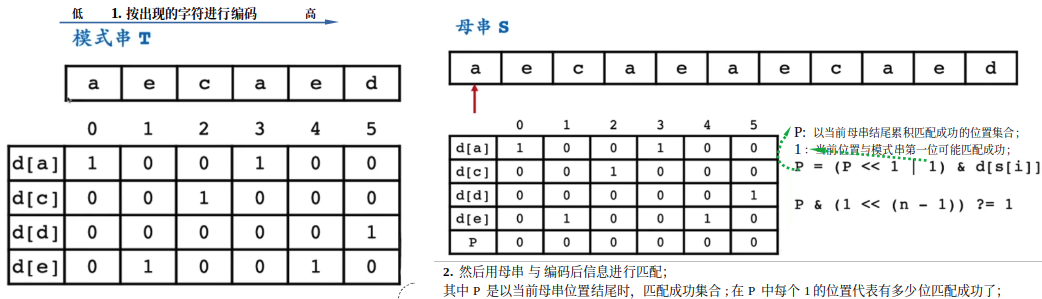
4. ShiftAnd：将模式串转换成信息编码，然后比较母串与信息串

　　这里有点类似拿一个打卡条，然后对着一位位去比较，match就为1，否则为0， 然后不断向后移动；

　　对于大于32 位的数据，可以使用bitmap；

 

5. 马拉车(Manacher)算法: 针对回文子串判断；

        a). 预处理：避免回文串长度为偶数；
            　　aba -> #a#b#a#
 　　           abab-> #a#b#a#b#
        b). 针对字符串进行回文串匹配操作，记录每个点对应的最大回文字节半径，然后根据最大半径的长度可以根据对称性,减少这个对称位置的判断过程;

　　　  对于当前位置是否有对应已判断过的点有以下3中情况：其中 i / j 为 当前最远回文位置对应的P 的对称点，P 点半径为len[p];　　

　　　　　　1). i / j 位置没有在已匹配过的回文串内，只能使用暴力;　

　　　　　　2). i / j 在已判断的回文串范围内，并且j 对应回文半径小于等于P 的回文范围内；

　　　　　　3). i / j 在已判断的回文串范围内，并且j 对应回文半径大于等于P 的回文范围内；

　　　　　　　　

 　　　　　　5. 最长回文子串　： 标准Manacher 题目：

class Solution {
public:
    string preprocess(string s) {
        string ret = "#";
        for(int i = 0; s[i]; ++i) ret = ret + s[i] + "#";
        return ret;
    }

    string longestPalindrome(string s) {
        string ns = preprocess(s), ans = "";
        int len = ns.size(), l = 0, r = 0;
        vector<int> radius(len, 0);

        int ret = 0;
        for(int i = 0; ns[i]; ++i) {
            //判断当前点是否可以使用之前的判断结果；min 过程是为处理2/3 中情况
            if(i < r) radius[i] = min(radius[l + r - i], r - i);
            //对当前位置进行判断；
            while(i - radius[i] > 0 && ns[i - radius[i] - 1] == ns[i + radius[i] + 1]) radius[i]++;
            //判断是否更新 l / r;
            if(i + radius[i] > r) r = i + radius[i], l = i - radius[i];
            //判断结果；
            if(radius[ret] < radius[i]) ret = i;
        }

        for(int i = ret - radius[ret], I = ret + radius[ret]; i <= I; ++i) {
            if(ns[i] == '#') continue;
            ans += ns[i];
        }
        return ans;
    }
};

 

6. 字典树(Trie) 与 双数组字典树（double Array Trie):

 

======================= **代码演示** =======================

1. 上面bruteForce/KMP/Sunday/shiftAnd 基本代码过程：

//#include "string_match.h"
#include <iostream>
#include <cstring>
using namespace std;

#define MAX_N 1000
#define CHAR_LEN 256
#define TESTFUNC(func, s1, s2) printf("func:%15s, idx:%3d\n", #func, func(s1,s2))
int brute_force(const char* text, const char* pattern) {
    for(int i = 0; text[i]; ++i) {
        bool flag = 1;
        for(int j = 0; pattern[j]; ++j) {
            if(text[i + j] == pattern[j]) continue;
            flag = 0;
            break;
        }
        if(flag) return i;
    }
    return -1;
}

void getPre(const char* text, int *pre) {
    pre[0] = -1;
    for(int i = 1, j = -1; text[i]; ++i) {
        while(j != -1 && text[i] - text[j + 1]) j = pre[j];   //这以前j 都是前一个匹配位置
        if(text[i] == text[j + 1]) ++j;                       //这里才将j 设置为与当前i 匹配的位置 ,如果没有匹配则为-1
        pre[i] = j;
    }
    return;
}
int getNextj(const char ch, const char* pattern, int *preMatch, int j) {
    while(j != -1 && ch - pattern[j + 1]) j = preMatch[j];
    if(ch == pattern[j + 1]) j++;                         
    return j;
}

//算法核心:在于对于模式串进行分析，找出模式串中每个index 中前面匹配的位置(以当前位置为结尾时，模式串前n位 与 当前结尾处前n位一致)
//         这样当某个位置不匹配时候，只要找模式串当前失配位置前一个值对应前置匹配的index 继续比较；
//编程技巧: 定义一个前置节点，作为一个万能匹配位置
//          对于母串匹配中的节点位置，不会倒回去
//          模式串前置匹配数组初始化：这里重点在于j 表示的是当前位置i 为结尾时，前缀n == 后缀n  对应的index 位置
int KMP(const char *text, const char *pattern) {
    int n = strlen(pattern);
    int *preMatch = (int *)malloc(sizeof(int) * n);
    getPre(pattern, preMatch);

    for(int i = 0, j = -1; text[i]; i++) {
//        while(j != -1 && text[i] - pattern[j + 1]) j = preMatch[j];  //这之前的j 都是表示i - 1 位置对应匹配patter 中的位置
//        if(text[i] == pattern[j + 1]) j++;                           //这里才更新了当前text[i] 对应到pattern 中 j 的值
//将上面过程变成getNextj, 相当于每次输入一个值，就会更新一次状态,类似状态机的过程；
        j = getNextj(text[i], pattern, preMatch, j);  
        if(pattern[j + 1] == '\0') return i - j;
    }
    return -1;
}

int SUNDAY(const char* text, const char* pattern) {
    //所有可能字符串对应last position，即使模式串只包含26字母,但是字符串结尾是'\0'，所以last_pos也必须保证有'\0';
    int *last_pos = (int *)malloc(sizeof(int) * CHAR_LEN),  
        n = strlen(text), m = strlen(pattern);
    for(int i = 0; i < CHAR_LEN; ++i) last_pos[i] = -1;
    for(int i = 0; pattern[i]; ++i) last_pos[pattern[i]] = i;
    bool flag = 1;
    for(int i = 0; i + m <= n; i += (m - last_pos[text[i + m]])) {
        flag = 1;
        for(int j = 0; pattern[j]; ++j) {
            if(text[i + j] == pattern[j]) continue;
            flag = 0;
            break;
        }
        if(flag) return i;
    }
    return -1;
}


int ShiftAnd(const char *text, const char *pattern) {
    //模式串长度小于32;
    unsigned int P = 0, code[CHAR_LEN] = {0};
    int n = 0;
    for(; pattern[n]; ++n) code[pattern[n]] |= (1 << n);

    for(int i = 0; text[i]; ++i) {
        P = (P << 1| 1) & code[text[i]];   //这里就是getNextP 过程；
        if(P & (1 << (n- 1))) return (i - n + 1);
    }
    return -1;
}


int main()
{
    char text[MAX_N], pattern[MAX_N];
    while(~scanf("%s %s", text, pattern)) {
        TESTFUNC(brute_force, text, pattern);
        TESTFUNC(KMP, text, pattern);
        TESTFUNC(SUNDAY, text, pattern);
        TESTFUNC(ShiftAnd, text, pattern);
    }
    return 0;
}

======================= **经典问题** =======================

1.KMP 中主要分为求模式串预处理过程，预处理后使用过程；很多时候是对于这两点分别考察的；

　　 459. 重复的子字符串 :

class Solution {
public:
    bool repeatedSubstringPattern(string s) {

        vector<int> pre(s.size(), -1);
        for(int i = 1, j = -1; s[i]; ++i) {
            while(j != -1 && s[i] - s[j + 1]) j = pre[j];
            if(s[j + 1] == s[i]) pre[i] = ++j;
        }

        //这里隐藏着前缀 与 后缀之间差值,如果可以被字符长度除尽，那么字符一定是以这部分差重复的；可以自己证明下
        return pre.back() != -1 && !(s.size() % (s.size() - 1 - pre.back()));
//brute force
//        int pos = 0;
//        while((pos = s.find(s[0], pos + 1)) != s.npos) {
//            if(s.size() % pos) continue;
//            int flag = 1;
//            for(int i = pos; s[i];) {
//                for(int j = 0; j < pos; ++j) {
//                    if(s[i] == s[j]) {
//                        i++;
//                        continue;
//                    }
//                    flag = 0;
//                    break;
//                }
//                if(!flag) break;
//            }
//            if(flag) return true;
//        }
//        return false;
    }
};

 　　1392. 最长快乐前缀  ：  

class Solution {
public:
    string longestPrefix(string s) {
        vector<int> pre(s.size(), -1);
        for(int i = 1, j = -1; s[i]; ++i) {
            while(j != -1 && s[i] - s[j + 1]) j = pre[j];
            if(s[j + 1] == s[i]) j++;
            pre[i] = j;
        }
        return s.substr(0, pre.back() + 1);
    }
};

 　　214. 最短回文串 ： 对于回文串，从前向后 与 从后向前都是一样，利用这一性质去掉满足回文的部分（也就是去掉重复的过程）；

class Solution {
public:
    string shortestPalindrome(string s) {
        if(!s.size()) return s;
        string reverse_s = s, temp_s = "";
        reverse(reverse_s.begin(), reverse_s.end());
        //下面操作是解题的精髓,利用了下面几个特性；
        //1.回文串自身性质是正着读/反着读都是一样的信息；
        //2.将s 取反后，回文串部分顺序没有变化，那么回文串部分是能找到重复的;
        //即可利用KMP 中对模式串的预处理过程；
        //3. 编程技巧，中间'#'; Exam: aaaaaa
        temp_s = s + '#' + reverse_s;  

        vector<int> pre(temp_s.size(), -1);
        for(int i = 1, j = -1; temp_s[i]; ++i) {
            while(j != -1 && temp_s[j + 1] - temp_s[i]) j = pre[j];
            if(temp_s[i] == temp_s[j + 1]) j++;
            pre[i] = j;
        }

        int pos = pre.back() + 1;
        s = temp_s.substr(pos, s.size() - pos);
        return  reverse_s + s;
    }
};

 

2. 标准求匹配字符串题： 

　　28. 实现 strStr()

class Solution {
public:
    void getNext(string pat, vector<int>& next){
        for(int i = 1, j = -1, I = next.size(); i < I; ++i) {
            while(j != -1 && pat[i] - pat[j + 1]) j = next[j];
            if(pat[i] == pat[j + 1]) ++j;
            next[i] = j;
        }
        return;
    }

    int KMP(string src, string pat) {
        int m = pat.size();
        vector<int> next(m, -1);
        getNext(pat, next);
        for(int i = 0, j = -1, I = src.size(); i < I; ++i){
            while(j != -1 && src[i] - pat[j + 1]) j = next[j];
            if(src[i] == pat[j + 1]) ++j;
            if(j == m - 1) return i - j;
        }
        return -1;
    }

    int Sunday(string src, string pat) {
#define MAX_CHAR 256
        int m = pat.size();
        vector<int> last_pos(MAX_CHAR, -1);
        for(int i = 0; i < m; ++i) last_pos[pat[i]] = i;

        for(int i = 0, I = src.size() - m; i <= I; i += (m - last_pos[src[i + m]])) {
            int flag = 1;
            for(int j = 0; j < m; ++j) {
                if(src[i + j] == pat[j]) continue;
                flag = 0;
                break;
            }
            if(flag) return i;
        }
        return -1;
    }

    void leftShift(vector<unsigned int>& P, int val) {
        int size = P.size();
        P[size - 1] = P[size - 1] << 1;
        for(int i = size - 2; i >= 0; --i) {
            if(P[i] & 0x80000000) P[i + 1] |= 1;
            P[i] = P[i] << 1;
        }
        P[0] |= 1;
        return;
    }

    int shiftAnd(string src, string pat) {
        int m =  pat.size(), granularity = sizeof(int) * 8;
        int cnt = ceil(m / double(granularity)), last_shift = (m % granularity ? m % granularity - 1: granularity - 1);
#define BASE 256
        vector<vector<unsigned int>> code(BASE, vector<unsigned int>(cnt, 0));
        for(int i = 0; i < m; ++i) {
            int ind = i / granularity, shift = i % granularity;
            code[pat[i]][ind] |= 1 << shift;
        }
#undef BASE
        vector<unsigned int> P(cnt, 0);
        for(int i = 0, I = src.size(); i < I; ++i) {
            leftShift(P, 1);
            for(int j = 0; j < cnt; ++j) P[j] = P[j] & code[src[i]][j];
            if(P[cnt - 1] & (1 << last_shift)) return i - m + 1;
        }
        return -1;
    }

    int strStr(string haystack, string needle) {
        if(!needle.size()) return 0;
        return KMP(haystack, needle);
        //return Sunday(haystack, needle);
        //return shiftAnd(haystack, needle);
    }
};

 

3. sunday 算法中对于字符串黄金对齐点的应用；

　　3. 无重复字符的最长子串

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(!s.size()) return 0;
        int pre = -1, ans = 0, n = s.size();
        vector<int> index(256, -1);
        for(int i = 0; i < n; ++i) {
            //当前字符在当前计算范围内出现了，就要更新pre节点 与 ans;
            if(index[s[i]] > pre) {
                ans = max(ans, i - 1 - pre);
                pre = index[s[i]];
            }
            index[s[i]] = i;
        }
        ans = max(ans, n - 1 - pre);
        return ans;
    }
};

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int ret = 0, before = -1;
        vector<int> last(256, -1);
        for(int i = 0, I = s.size(); i < I; ++i) {
//优化，每次算下当前字符是否重复过，如果重复就要更新 before
//减少if 判断过程，时间有减少
            before = max(before, last[s[i]]);
            last[s[i]] = i;
            ret = max(ret, i - before);
        }
        return ret;
    }
};

 

4. 面试题 17.17. 多次搜索 ： 多次匹配问题；

class Solution {
public:
    //KMP : 
    vector<int> KMP(string src, string pat) {
        int len_p = pat.size();
        if(!len_p) return vector<int>();
        vector<int> pre(len_p, -1), ret;
        for(int i = 1, j = -1; i < len_p; ++i) {
            while(j != -1 && pat[j + 1] != pat[i]) j = pre[j];
            if(pat[j + 1] == pat[i]) j += 1;
            pre[i] = j;
        }

        for(int i = 0, j = -1; i < src.size(); ++i) {
            while(j != -1 && src[i] != pat[j + 1]) j = pre[j];
            if(src[i] == pat[j + 1]) j += 1;
            if(j == len_p - 1) {
                ret.push_back(i - j);
                j = pre[j];
            }
        }
        return ret;
    }
    
    //Sunday:
    vector<int> Sunday(string& src, string& pat) {
        int len_p = pat.size(), len_s = src.size();
        if(!len_p) return vector<int>();
#define BASE 128
        vector<int> last(BASE, -1), ret;
        for(int i = 0; i < len_p; ++i) last[(pat[i])] = i;
        for(int i = 0, I = len_s - len_p; i <= I; i += (len_p - last[(src[i + len_p])])) {
            int j = 0;
            while(j < len_p && src[i + j] == pat[j]) j += 1;
            if(j == len_p) ret.push_back(i);
        }
#undef BASE
        return ret;
    }

    //Shift-And: 这个长度1000，比较麻烦
    vector<vector<int>> multiSearch(string big, vector<string>& smalls) {
        vector<vector<int>> ret;
        for(auto x : smalls) {
            ret.push_back(KMP(big, x));
//            ret.push_back(Sunday(big, x));
        }
        return ret;
    }
};

 

======================= **应用场景** =======================

KMP：本质是一个状态机，它的状态就是每次匹配后得到的子串对应位置(j 值）；根据每次输入的一个母串字符，得到更新后的状态；

　　在KMP 算法中，对于母串匹配过程,不会有回退过程（就是程序中getNextj部分）；

　　针对这一特点，KMP可以用于流文件以及一些大文件的单模式匹配，比较适合。因为每次只需要匹配当前字符，不用存储所有的母串；

　　时间复杂度位 n + m(极限情况位n * m);

 

SUNDAY:

　　在文章中查找单词，最优情况下，时间复杂度O(n / m) (n:母串长度, m:模式串长度)，远优于bruteForce, KMP;

　　但是没有办法处理流数据，因为需要存储相当一部分母串信息；

 

ShiftAnd：

　　时间复杂度O(n), 支持流数据处理，类比KMP 算法， shiftAnd 更高效，天生支持正则的多模式匹配；每行可以存在多种匹配；

　　同样也诠释了自动机思想，每次进入一个字符，更新状态；

 　 EXAM： 正则表达式：（a|b|c) & (c|d) & e & (f|a|b), 用shiftAnd 方法很方便，编码后的信息如下；

 　　　　　　

 

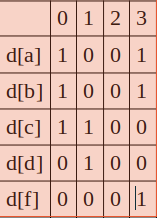
 题外话：关于自动机，主要用于编译原理；但是自动机本质就是图灵机，也就是当代计算机的基础；