AVL-平衡二叉搜索树(Self-balancing binary search tree)

======================= **基础知识** =======================

二叉排序树（二叉搜索树）：思维结构中可以是有序数组，树；

　　性质： 左子树  < 根节点 ； 右子树  > 根节点；

　　　　　　中序遍历结果：就是递增排序的有序序列；(3,17, 20, 28, 28, 29, 30, 32)

　　　　　

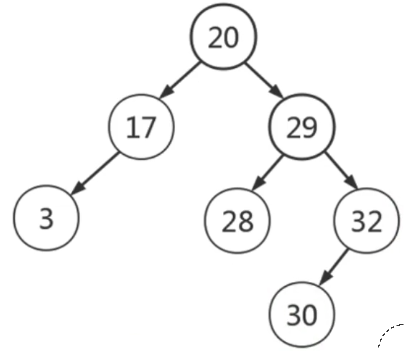
 　　操作：

　　　　增（插入）： 与根结点比较：小于:进入左子树；大于:进入右子树；重复操作，直到找到一个空节点插入该数；

　　　　查：与根节点比较，小于进入左子树，大于进入右子树，直到找到该数；

　　　　删：对应多种情况，分类处理；

　　　　　　1.删除叶子节点：直接删除；

　　　　　　2.删除度为1 的节点： 只要存在上一个根节点，直接将孩子顶替当前被删除的节点；

　　　　　　3. 删除度为2 的节点： 前驱节点 ：相对删除节点，左子树中离他最近的节点（左子树一直往右），左子树中最大值；

　　　　　　　　　　　　　　　　后置节点： 相对删除节点，右子树中离他最近的节点（右子树一直往左），右子树中最小值；

　　　　　　　　　　对于前驱/后置节点：它们最多为度为1 的节点；如果度为2 ，一定存在左右子树，那就不会是当前子树中最值；

　　　　　　　　　　所以就可以把前驱（后置）节点替换删除节点，然后将问题转换为删除度为1/0 的操作；

 　　　　　　　　

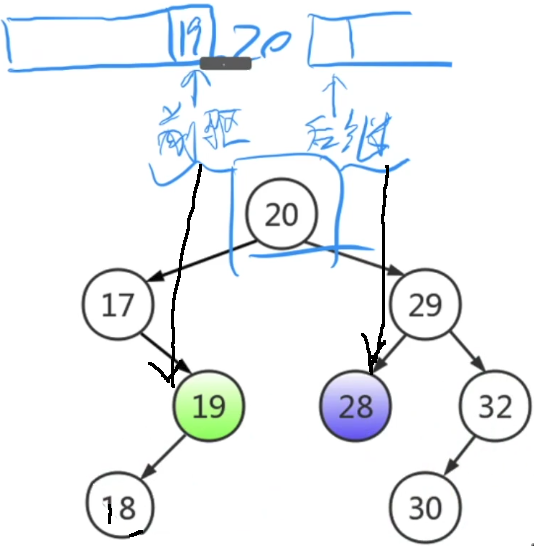
　　缺点： 二叉排序树，有可能退化成如下的链表，使得所有的操作时间复杂度变成O(n);

　　　　　　　　

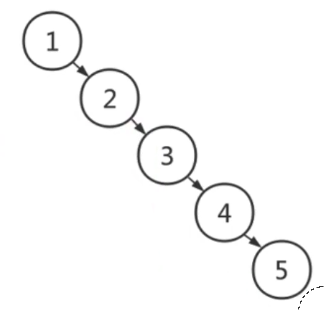
　　用途： 用于解决排名相关的检索需求；

 

AVL 树：平衡二叉排序树：重点在于平衡条件！！

AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An algorithm for the organization of information》中发表了它。

　　性质：除了上面的二叉排序树的性质以外： | H(left) - H(right) | <= 1;  左右子树的高度差不超过1；

　　优点：对于每个节点的左右子树的树高做了限制，所以整个树不会退化成链表；

　　特点：对于AVL 树的旋转操作，它使得一部分树高 - 1， 一部分树高 + 1， 还有一部分树高不变；这一特点使得平衡调整有可能成功；

　　基本操作：　

　　　　　　左旋： 以k1 为基点，将k3 点左旋上来；A 节点变成K1 的右子树；

　　　　　　右旋： 左旋的反向操作：

　　　　　　左/右旋操作后，仍然保证了二叉排序的性质；

　　　　　　

　　　　

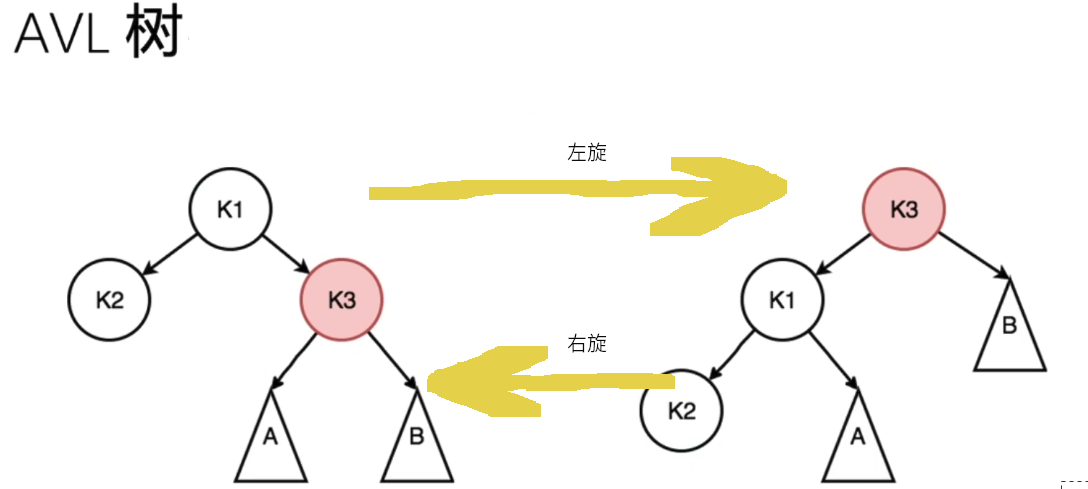
　　　　在增删改查操作中，只有增/删 会有可能引起AVL 树失衡；

　　　　在增/删 以后的递归回溯过程中，在当前节点向下看，如果AVL 树失衡，为了维护AVL 树的性质，就需要进行调整；调整可能会进行多次；

　　　　经典的AVL 树 -失衡类型： 主要3大类： LL/RR型，LR型，RL 型；注意：删除/插入操作，每次只会增加（减少）一个节点，而原树也是AVL 树，这也是下面公式推导中要注意的点；

　　　　　　LL/RR 型： 在K1节点向下看, 左子树K2节点高(L); 在K2节点中，左子树A节点高(L);

　　　　　　解决方案：LL ： 抓住K1 大右旋，将K2 旋转上来； RR： 直接抓住K1 大左旋；

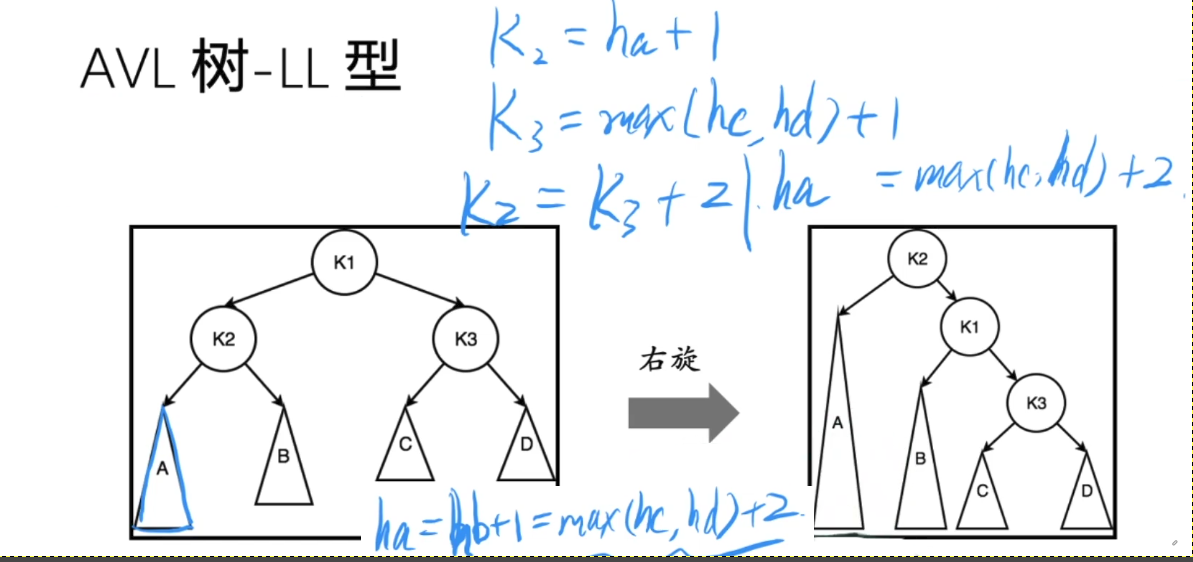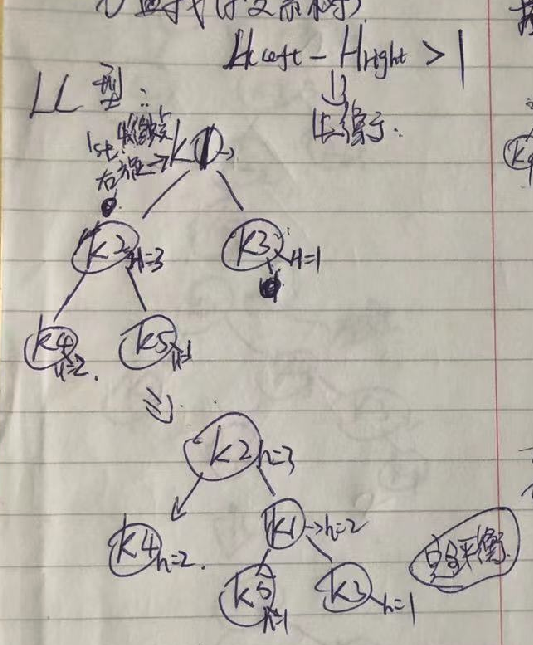　　　　　　      LL型：   RR型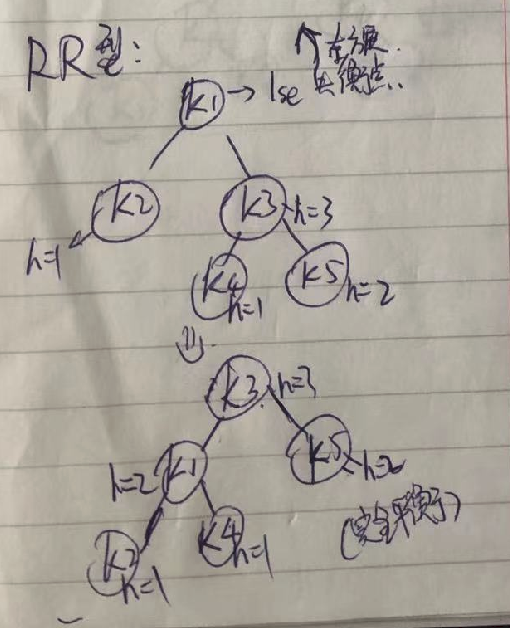

　　　　　　LR 型： 在K1节点向下看, 左子树K2节点高(L); 在K2节点中，左子树K3节点高(R); 　

　　　　　　　　解决方案： 先抓K2左旋，变成LL 型； 然后再抓K1 右旋；

 

  　　　　　  RL 型： 与LR 型相反；

　　　　　　　　解决方案： 与LR 型相反，先小右旋，变成RR型； 再大左旋；

　　　　　　

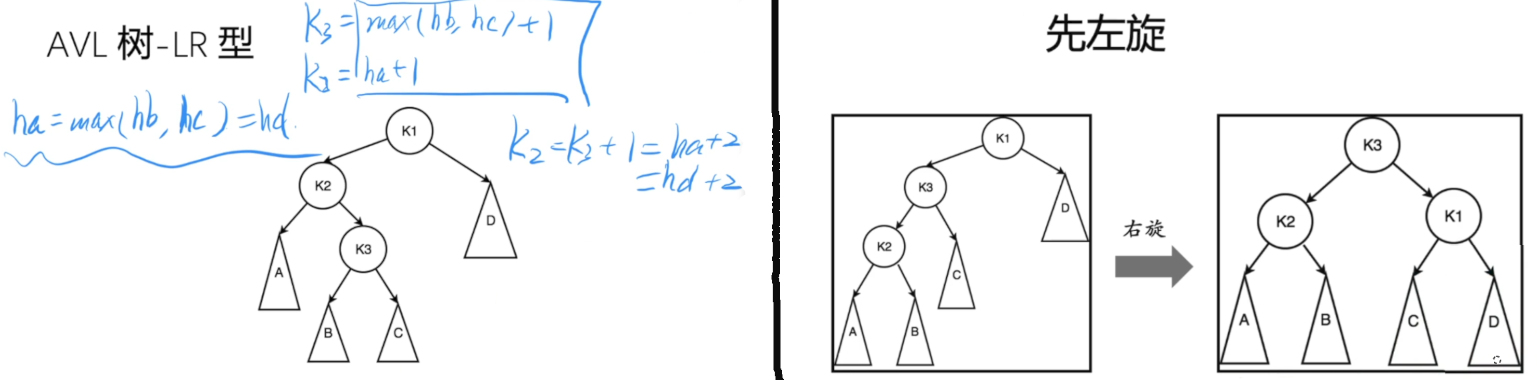
　　　　对于LR/RL 类型旋转的过程： 

　　LR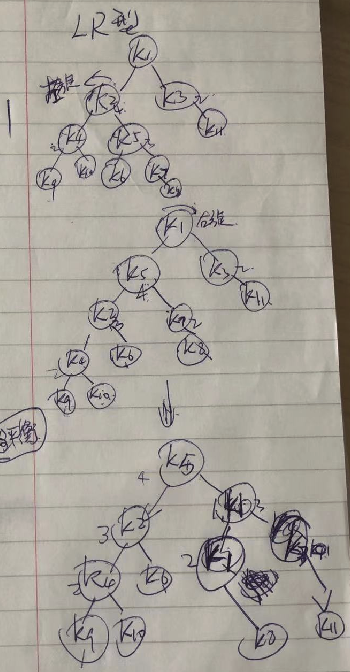型：　RL型：

======================= **代码演示** =======================

数据结构是定义一种性质，并维护这种性质；

1. 实现二叉排序树：代码中注意对于erase 的删除部分的处理，尤其是对于度为2 节点的删除；插入/删除过程返回更新后的节点；

//#include "binaryTree.h"
#include <iostream>
using namespace std;

struct Node{
    Node(int key = 0, Node *left = nullptr, Node *right = nullptr)
        : key(key), left(left), right(right) {}
    int key;
    Node *left, *right;

};

Node *getNewnode(int key) {
    return new Node(key);
}

Node *insert(Node *root, int key){    //返回插入新节点以后的root 地址
    if(root == nullptr) return getNewnode(key);
    if(root->key == key) return root;

    if(key < root->key) root->left = insert(root->left,key);  //这里就用到返回值,减少操作，多体会
    if(key > root->key) root->right = insert(root->right,key);
    return root;
}

Node *predeccessor(Node *root) {  //左子树最大值
    Node *temp = root->left;
    while(temp->right) temp = temp->right;
    return temp;
}

Node *erase(Node *root, int key) {
    if(root == nullptr) return root;
    if(key < root->key) root->left = erase(root->left, key);
    else if(key > root->key) root->right = erase(root->right, key);
    else {
//        if(root->left == nullptr && root->right == nullptr){ //度为0
//            delete root;
//            return nullptr;
        if( root->left == nullptr || root->right == nullptr){//度为1
            Node *temp = root->left ? root->left : root->right;
            delete root;
            return temp;
        } else {
            Node *temp = predeccessor(root);
            root->key = temp->key;
            root->left = erase(root->left, temp->key);
        }
    }
    return root;
}

void clear(Node *root)  {
    if(root == nullptr) return;
    clear(root->left);
    clear(root->right);
    delete root;
    return;
}

void output(Node *root) {
    if(!root) return;
    output(root->left);
    cout << root->key << " ";
    output(root->right);
    return;
}

int main()
{
    int op, val;
    Node *root = nullptr;
    while(cin >> op >> val) {
        switch (op) {
            case 0 : root = insert(root, val); break;
            case 1 : root = erase(root, val); break;
        }
        output(root);
        cout << endl;
    }
    return 0;
}

//input :
//0 3
//0 2
//0 1
//0 5 
//0 4 
//1 3
//1 4

#include <iostream>
using namespace std;

struct Node {
    Node(int v = -1, Node *l = nullptr, Node *r = nullptr) : val(v), left(l), right(r){}
    Node *left, *right;
    int val;
};

class BinaryTree{
    private:
        Node *root;
        void clear(Node *root){
            if(!root) return;
            if(root->left) clear(root->left);
            if(root->right) clear(root->right);
            delete root;
            return;
        }

        Node *__insert(Node* r, int key) {
            if(!r) return new Node(key);
            if(key < r->val) r->left  = __insert(r->left, key);
            else if(key > r->val) r->right = __insert(r->right, key);
            return r;
        }

        Node *__find(Node *r, int key) {
            if(!r) return nullptr;
            if(key < r->val) return __find(r->left,  key);
            else if(key > r->val) return __find(r->right, key);
            return r;
        }

        Node *predeccessor(Node *r) { //后驱节点
            Node *temp = r->right;
            while(temp->left) temp = temp->left;
            return temp;
        }

        Node *__erase(Node *r, int key) {
            if(!r) return nullptr;

            if(key < r->val) r->left  = __erase(r->left , key);
            else if(key > r->val) r->right = __erase(r->right, key);
            else {
                if(!r->left || !r->right) {
                    Node *son = r->left ? r->left : r->right;
                    delete r;
                    return son;
                } else {
                    Node *__predec = predeccessor(r);
                    r->val = __predec->val;
                    r->right = __erase(r->right, __predec->val);
                }
            }
            return r;
        }

        void __output(Node *r) {
            if(!r)  return;
            __output(r->left);
            cout << r->val << " ";
            __output(r->right);
            return;
        }


    public:
        BinaryTree(Node *pn) = delete;
        BinaryTree(int key) {
            root = new Node(key);
        }
        //copy/move ...
        ~BinaryTree() {
            clear(root);
        }
        
        void insert(int key) {
            root = __insert(root, key);
            return;
        }

        void erase(int key){
            root = __erase(root, key);
            return;
        }

        Node *find(int key){
            return __find(root, key);
        }

        void output() {
            __output(root);
            return;
        }

};

int main()
{
    int op, val;
    BinaryTree *pbt = nullptr;
    while(cin >> op >> val) {
        switch(op) {
            case 0: {
                        if(!pbt) pbt = new BinaryTree(val);
                        else pbt->insert(val);
                        break;
                    }
            case 1: {
                        if(pbt) pbt->erase(val);
                        break;
                    }
        }
        pbt->output();
        cout << endl;
    }
    return 0;
}

 

2. AVL树 代码实现：代码中注意点：虚拟空节点的引入，优化程序（虚拟空节点的 代码技巧）；

　　　　　　　　　　　　　　　　对于每个变化的节点都要重新更新深度；左旋/右旋/插入/删除

　　　　　　　　　　　　　　　　以及上面二叉排序树中的注意点；

//input
//0 5
//0 9
//0 8
//0 3
//0 2
//0 4
//0 1 
//0 7
//1 8
//1 1
//1 5


#include <iostream>
using namespace std;

#define NIL (&Node::__NIL)

struct Node {
    Node(int k = 0, int h = 0,  Node *l = NIL, Node *r = NIL) 
        : key(k), h(h), left(l), right(r) {}
    int key, h;
    Node *left, *right;
    static Node __NIL;  //这里只是声明
};

Node Node::__NIL;  //对于静态变量的使用,这里才是定义

Node *getNewNode(int key) {
    return new Node(key,1);
}

void clear(Node *root) {
    if(root == NIL) return;
    clear(root->left);
    clear(root->right);
    cout << "del root key: " << root->key << endl;
    delete root;
    return;
}

void update_height(Node *root) {
    //NIL if(root->left = nullptr  && root->right == nullptr) return;
    //NIL if(root->left == nullptr) root->h = root->right->h + 1;
    //NIL else if(root->right == nullptr) root->h = root->left->h + 1;
    root->h = max(root->left->h, root->right->h) + 1;
    return;
}

Node *left_rotate(Node *root){
    Node *new_root = root->right;
    root->right = new_root->left;
    new_root->left = root;
    update_height(root);
    update_height(new_root);
    return new_root;
}

Node *right_rotate(Node *root){
    Node *new_root = root->left;
    root->left= new_root->right;
    new_root->right= root;
    update_height(root);
    update_height(new_root);
    return new_root;
}

const char *Type[5] = {"", "LL", "RR", "LR", "RL"};

Node *maintain(Node *root) {
    if(abs(root->left->h - root->right->h) < 2) return root;
    int type = 0;
    if(root->left->h > root->right->h) {
        if(root->left->right->h > root->left->left->h) {
            //lr
            printf("%d : left rotate\n", root->left->key);
            type = 3;
            root->left = left_rotate(root->left);
        }
        //ll
        if(!type) type = 1;
        printf("%d : right rotate\n", root->key);
        root = right_rotate(root);
    }else {
        if(root->right->left->h > root->right->right->h) {
            //rl
            type = 4;
            printf("%d : right rotate\n", root->right->key);
            root->right = right_rotate(root->right);
        }
        //rr
        printf("%d : left rotate\n", root->key);
        if(!type) type = 2;
        root = left_rotate(root);
    }
    printf("maintian the type = %s;\n", Type[type]);
    return root;
}

Node *insert(Node *root, int key) {
    if(root == NIL) return getNewNode(key);
    if(root->key == key) return root;

    if(key < root->key) root->left = insert(root->left, key);
    else  root->right = insert(root->right, key);
    update_height(root);
    return maintain(root);
} 

Node* predeccesor(Node *root) {
    Node *temp = root->left;
    while(temp->right != NIL) temp = temp->right;
    return temp;
}

Node *erase(Node *root, int key){
    if(root == NIL) return root;
    if(key < root->key) root->left = erase(root->left, key);
    else if(key > root->key) root->right = erase(root->right, key);
    else {
        //删除节点数为0 或 1 的节点
        if(root->left == NIL || root->right == NIL) {
            Node *temp = root->left == NIL ? root->right : root->left;
            delete root;
            return temp;
        }else {  //删除节点数为2 , 这里使用左子树最右边的值替补被删除的数（也可以通过右子树最左边的值替补被删除的值）
            Node *temp = predeccesor(root);
            root->key = temp->key;
            root->left = erase(root->left, temp->key);
        }
    }
    update_height(root);
    return maintain(root);
}

void print(Node *root) {
    printf("(%d[%d] | %d, %d)\n", root->key, root->h, root->left->key, root->right->key);
    return;
}

void output(Node *root) {
    if(root == NIL) return;
    print(root);
    output(root->left);
    output(root->right);
    return;
} 

int main()
{
    int op, val;
    Node *root = NIL;
    while(cin >> op >> val) {
        cout << endl << "====AVL tree print ====" << endl;
        switch (op) {
            case 0 : {
                        printf("insert %d\n", val);
                         root = insert(root, val); break;
                     }
            case 1 : {
                        printf("erase the %d\n", val);
                         root = erase(root, val); break;
                     }
        }
        output(root);
        cout << "====tree print end====" << endl;
    }

    clear(root);

    return 0;
}

======================= **经典问题** =======================

1. 前驱/后继的求取： 面试题 04.06. 后继者 : 非常好的锻炼结构化思维的例题！； 使用pre 记录前一个节点值，代码技巧；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* pre;
    TreeNode *inOrder(TreeNode *r, TreeNode *p)  {
        if(!r) return nullptr;
        TreeNode *ans = nullptr;
        if(ans = inOrder(r->left, p)) return ans;
        if(pre && pre == p) return r;
        pre = r;  //精髓
        return inOrder(r->right, p);
    }

    TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
//利用二叉树结构化思维方式求解
        pre = nullptr;
        return inOrder(root, p);
// 利用二叉排序树性质求解
//        TreeNode *ans = nullptr;
//
//        if(p->val < root->val) ans = inorderSuccessor(root->left, p);
//        else if(p->val > root->val) return inorderSuccessor(root->right, p);
//        else {
//            if(!root->right) return nullptr;
//            TreeNode *next = root->right;
//            while(next->left) next= next->left;
//            return next;
//        }
//        if(!ans) ans = root;
//        return ans;
    }
};

 2. 450. 删除二叉搜索树中的节点 : BST 删除节点的裸题：对于不同度的节点处理；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode *predecessor(TreeNode *root){
        TreeNode *temp = root->left;
        while(temp->right) temp = temp->right;
        return temp;
    }

    //这题目就是BST 中删除指定节点操作
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(!root) return nullptr;

        if(key < root->val) root->left = deleteNode(root->left, key);
        else if(key > root->val) root->right = deleteNode(root->right, key);
        else {
            //出度为0 或 1
            if(root->left == nullptr || root->right == nullptr) {
                TreeNode *temp = root->left ? root->left : root->right;
                delete root;
                return temp;
            } else {
                //出度为2
                TreeNode *temp = predecessor(root);
                root->val = temp->val;
                root->left = deleteNode(root->left, temp->val);
            }
        }
        return root;
    }
};

 

3.对于树类型数据，结构化思维是很重要的一种手段；上面的AVL 树的代码实现中也利用了结构化思维来实现；

 结构化思维训练：

501. 二叉搜索树中的众数  : 结构化思维；这里对于最后节点需要判断情况下，避免重复代码有很好示范；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//这里对于减少最后节点判断过程，做了一个不错的示范；
class Solution {
public:
    int max_cnt, cnt, pre_val;
    vector<int> ans;

    void __inorder(TreeNode* root) {
        if(!root) return;
        __inorder(root->left);

        if(pre_val == root->val) cnt++;
        else {
            cnt = 1;
            pre_val = root->val;
        }

        //这里是为了解决最后一个节点,不用单独写一份判断过程;
        if(cnt == max_cnt) {
            ans.push_back(pre_val);
        } else if(cnt > max_cnt) {
            max_cnt = cnt;
            ans.clear();
            ans.push_back(pre_val);
        }

        __inorder(root->right);
        return;
    }

    vector<int> findMode(TreeNode* root) {
        pre_val = root->val,    //体会这样做的好处
                max_cnt = 0, cnt = 0;
        ans.clear();

        __inorder(root);
        return ans;
    }
};


//original
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int cnt, max_cnt;
    TreeNode *pre;

    void findMax(TreeNode *root, vector<int> &ans){
        if(!root) return;

        findMax(root->left, ans);
        if(!pre) cnt = 1;
        else {
            if(pre->val == root->val) cnt++;
            else{
                if(cnt >= max_cnt) {
                    if(cnt > max_cnt) ans.clear(), max_cnt = cnt;
                    ans.push_back(pre->val);
                }
                cnt = 1;
            }
        }
        pre = root;

        findMax(root->right, ans);
        return;
    }

    vector<int> findMode(TreeNode* root) {
        cnt = max_cnt = 0;
        pre = nullptr;
        vector<int> ans;
        findMax(root, ans);
        if(cnt < max_cnt) return ans;
        if(cnt > max_cnt) ans.clear();
        ans.push_back(pre->val);
        return ans;
    }
};

1382. 将二叉搜索树变平衡  :  二叉排序树的实现方式也有很多，在树结构中，很多时候使用结构性思维；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode *root, vector<TreeNode*> &nums) {
        if(!root) return;
        inorder(root->left, nums);
        nums.push_back(root);
        inorder(root->right, nums);
        return;
    }

    TreeNode *buildTree(vector<TreeNode*> &nums, int l, int r) {
        if(l > r) return nullptr;
        int ind = (l + r) >> 1;
        TreeNode *node = nums[ind];
        node->left = buildTree(nums, l, ind - 1);
        node->right = buildTree(nums, ind + 1, r);
        return node;
    }

    TreeNode* balanceBST(TreeNode* root) {
        vector<TreeNode*> nums;
        inorder(root, nums);
        return buildTree(nums,0, nums.size() - 1);
    }
};

108. 将有序数组转换为二叉搜索树  ： 结构化思维

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode *buildTree(vector<int> &nums, int l, int r) {
        if(l > r) return nullptr;
        int mid = (l + r + 1) >> 1;
        TreeNode *new_node = new TreeNode(nums[mid]);
        new_node->left = buildTree(nums, l , mid - 1);
        new_node->right = buildTree(nums, mid + 1, r);
        return new_node;
    }

    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return buildTree(nums, 0, nums.size() - 1);
    }
};

98. 验证二叉搜索树 ： 结构化思维， 甚至可以理解为就是for 循环遍历有序数组；

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode *pre;
    bool __isValidVBST(TreeNode *root) {
        if(!root) return true;
        if(!__isValidVBST(root->left)) return false;
        if(pre && pre->val >= root->val)  return false;
        pre = root;
        if(!__isValidVBST(root->right)) return false;
        return true;
    }
    bool isValidBST(TreeNode* root) {
        pre = nullptr;
        return __isValidVBST(root);
    }
};

 剑指 Offer 33. 二叉搜索树的后序遍历序列  : pre的使用在于它的定义，以及在结构化中的使用方式；与前/中/后 序都没任何关系；前/中/后序都可以用pre实现按顺序循环；

//结构化思维方式: 这里是为了表达pre对于结构化思维意义；
//当然这里pre初始值设定有缺陷(要取一个不在范围内值); leetcode 23 个test case 可以过；
//fail case： [-6, -3, 9, -5, -1]
class Solution {
public:
    int pre;
    bool __postorder(vector<int>& nums, int l, int r) {
        if(l >= r) return true;
        int ind = l;
        while(nums[ind] < nums[r]) ind++;
        if(!__postorder(nums, l, ind - 1)) return false;
        if(pre != -1 && nums[r] < pre) return false;
        pre = nums[r];
        if(!__postorder(nums, ind, r - 1)) return false;
        return true;
    }

    bool verifyPostorder(vector<int>& postorder) {
        pre = -1;
        return __postorder(postorder, 0, postorder.size() - 1);
    }
};

//orignial
class Solution {
public:

    bool checkPostorder(vector<int> &nums, int l, int r) {
        if(l >= r) return true;
        int ind = l;
        while(nums[ind] < nums[r]) ind++;
        if(!checkPostorder(nums, l, ind - 1) || !checkPostorder(nums, ind, r - 1)) return false;
        while(nums[ind] > nums[r]) ind++;
        return ind == r;
    }


    bool verifyPostorder(vector<int>& postorder) {
        return checkPostorder(postorder, 0, postorder.size() - 1);
    }
};

1008. 前序遍历构造二叉搜索树

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode *buildTree(vector<int> &nums, int l, int r) {
        if(l > r) return nullptr;
        int ind = l + 1;
        while(ind <= r && nums[ind] <= nums[l]) ind++;
        TreeNode *node =  new TreeNode(nums[l]);
        node->left = buildTree(nums, l + 1, ind - 1);
        node->right = buildTree(nums, ind, r);
        return node;
    }

    TreeNode* bstFromPreorder(vector<int>& preorder) {
        return buildTree(preorder, 0, preorder.size() - 1);
    }
};

 

 思维锻炼结果检验：

面试题 04.09. 二叉搜索树序列:  对于vector<vector<int>> 套娃式结构中，对于空节点的返回值为vector<vector<int>>{vector<int>()};

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void mergeSequence(vector<int>&l, int idx_l, vector<int>&r, int idx_r, vector<int> cur, vector<vector<int>> &ans) {
        if(idx_l == l.size() || idx_r == r.size()) {
            if(idx_l == l.size()) while(idx_r < r.size()) cur.push_back(r[idx_r++]);
            else while(idx_l < l.size()) cur.push_back(l[idx_l++]);
            ans.push_back(cur);
            return;
        }

        cur.push_back(l[idx_l]);
        mergeSequence(l, idx_l + 1, r, idx_r, cur, ans);
        cur.pop_back();
        cur.push_back(r[idx_r]);
        mergeSequence(l, idx_l, r, idx_r + 1, cur, ans);
        return;
    }


    vector<vector<int>> BSTSequences(TreeNode* root) {
        vector<vector<int>> ans;
        if(!root) {
            ans.push_back(vector<int>());  //对于vector<vector<int>>这类套圈的返回值对于nullptr 处理方案；
            return ans;
        }
        vector<vector<int>> pre = BSTSequences(root->left),
            next = BSTSequences(root->right);

        vector<int> cur{root->val};
        for(int i = 0, I = pre.size(); i < I; ++i) {
            for(int j = 0, J = next.size(); j < J; ++j) {
                mergeSequence(pre[i], 0, next[j], 0, cur, ans);
            }
        }
        return ans;
    }
};

//original
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    void merge(vector<vector<int>> &ans, vector<int>&now,
                vector<int> &l, int li, vector<int> &r, int ri) {

        if(li == l.size() && ri == r.size()) {
            ans.push_back(now);
            return;
        }

        if(li < l.size()) {
            now.push_back(l[li]);
            merge(ans, now, l, li + 1, r, ri);
            now.pop_back();
        }
        if(ri < r.size()) {
            now.push_back(r[ri]);
            merge(ans, now, l, li, r, ri + 1);
            now.pop_back();
        }
        return;
    }


    vector<vector<int>> BSTSequences(TreeNode* root) {
        vector<vector<int>> ans;
        if(!root) {
            ans.push_back(vector<int>());
            return ans;
        }

        vector<vector<int>> left = BSTSequences(root->left);
        vector<vector<int>> right = BSTSequences(root->right);

        vector<int> temp;
        temp.push_back(root->val);

        if(!left.size() && !right.size())  ans.push_back(temp);
        for(int i = 0; i < left.size(); i++) {
            for(int j = 0; j < right.size(); j++) {
                merge(ans, temp, left[i], 0, right[j], 0);
            }
        }

        return ans;
    }
};

======================= **应用场景** =======================

1. 单从数据类型来讲，AVL 是可以用来实现map/set 的功能的，但是因为AVL 是一种高度平衡二叉树，左右树高差不超过1；所以在不断插入/删除过程中，为了保证数据性质，需要不断进行旋转；在大量数据插入/删除，这一操作有可能会降低速度；

　　所以使用RB Tree(这是一种弱平衡二叉树，只要保证没有一条路径会是其他路径的2倍以上），旋转的次数会更少，所以在STL种使用了RB tree 作为其底层数据结构；

 

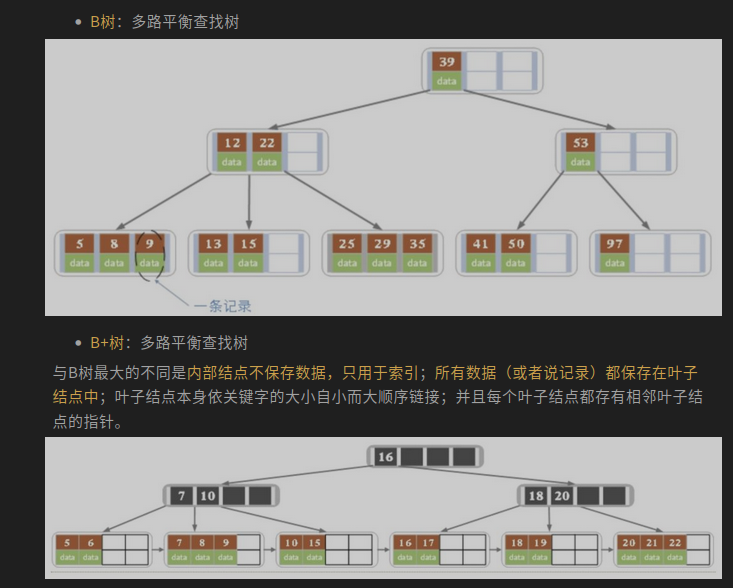
2. 类似的数据结构有： B树，B+树；都是针对具体的应用场景，对数据结构进行优化；

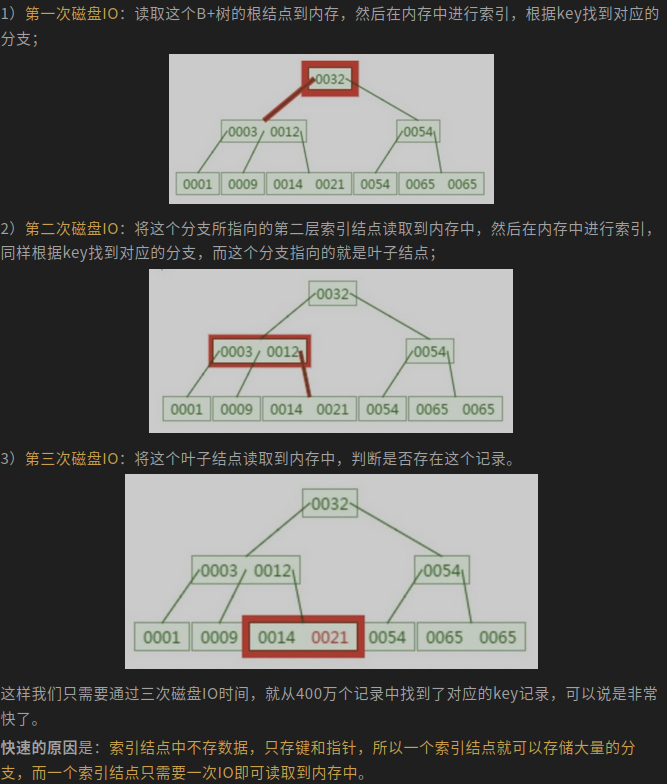
　　在实际存储引擎中一般都是使用B+ 树，这其中的原因与好处，下面文章写的很好，摘录部分信息；

数据存储技术：单机篇