经典排序算法(快排/归并） - 学海一扁舟

经典排序算法(快排/归并）

======================= **基础知识** =======================

排序算法重要性：问题系统熵决定了一个问题被解决的难易程度，排序可以有效降低熵值；

排序中有很多算法中都有分治的思想;

======================= **代码演示** =======================

1. 一些基本的排序方法及优化(选择，冒泡，插入排序，堆排序）；

　　注意边界条件，特别是递归中下一次递归的范围没有减少，就会陷入死循环中；

　　对于判断中使用 >= 还是 > , 至少要以遍历完所有的节点为基本要求，减少遗漏；有时候还会根据实际处理中保证各个分类部分的平衡等要求具体判断；

  1 #include <iostream>
  2 #include <vector>
  3 #include <algorithm>
  4 using namespace std;
  5 
  6 #define MAX_N 1000
  7 
  8 #ifdef DEBUG
  9 #define logmsg(frm, args...) printf(frm, ##args);
 10 #else
 11 #define logmsg(frm, args...)  1;
 12 #endif
 13 
 14 #define TEST_FUNC(func, arg, a...) vector<int> arg(nums);\
 15     start = clock();\
 16     func(arg, ##a);\
 17     elapseTime = (double (clock() - start)) / CLOCKS_PER_SEC;\
 18     printf("after %s, time is %f\n", #func, elapseTime);\
 19     for(auto x : arg)  len += logmsg("%4d", x);\
 20     logmsg("\n");
 21 
 22 void swap(int &a, int &b) {
 23     int t = a;
 24     a = b;
 25     b = t;
 26     return;
 27 }
 28 
 29 void selectionSort(vector<int> &nums, int l, int r) {
 30     while(l < r) {
 31         int min_idx = l, max_idx = r - 1;
 32         //必须要下面一行，以防最值在下面两步swap 中被移动了;
 33         if(nums[min_idx] > nums[max_idx]) swap(nums[min_idx], nums[max_idx]);
 34         for(int i = l; i < r; ++i) {
 35             if(nums[i] < nums[min_idx]) min_idx = i;
 36             if(nums[i] > nums[max_idx]) max_idx = i;
 37         }
 38         swap(nums[l], nums[min_idx]);
 39         swap(nums[r - 1], nums[max_idx]);
 40         l++;
 41         r--;
 42     }
 43     return;
 44 }
 45 
 46 
 47 //排序 从小到大, 区间 左闭右开
 48 void bubbleSort(vector<int> &nums, int l, int r) {  //O(n * n)
 49     for(int i = r - 1; i > l; --i) {
 50         bool sortedFlag = true;  //优化： 一旦某次遍历没有任何交换，意味着所有数字都已经有序了；
 51         for(int j = l; j < i; ++j) {
 52             if(nums[j] > nums[j + 1]) {
 53                 swap(nums[j], nums[j + 1]);
 54                 sortedFlag = false;
 55             }
 56         }
 57         if(sortedFlag) return;
 58     }
 59     return;
 60 }
 61 
 62 //insert sort 在小数量数据，并且基本排序完成的 时间复杂度较好，极限(已经排序好的数组）可以到O(n) 比较即可
 63 void insertSort(vector<int> &nums, int l, int r) { // O(n) ~ O(n * n);
 64     for(int i = l + 1; i < r; ++i) {
 65 //way2:减少swap 次数
 66 #ifndef WAY1
 67         int base = nums[i], j = i;
 68         while(j > l && nums[j - 1] > base){
 69             nums[j] = nums[j - 1];
 70             j--;
 71         }
 72         nums[j] = base;
 73 
 74 #else
 75 //way1:
 76         for(int j = i; j > l; --j) {
 77             if(nums[j] >= nums[j - 1]) break;
 78             swap(nums[j], nums[j - 1]);
 79         }
 80 #endif
 81     }
 82     return;
 83 }
 84 
 85 void unguardedInsertSort(vector<int> &nums, int l, int r) {
 86     int min_idx = l;
 87     for(int i = l + 1; i < r; ++i) if(nums[i] < nums[min_idx]) min_idx = i;
 88     while(min_idx > l) {
 89         swap(nums[min_idx], nums[min_idx - 1]);
 90         --min_idx;
 91     }
 92     for(int i = l + 2; i < r; ++i) {
 93 #ifndef WAY1
 94         int base = nums[i], j = i;
 95         while(nums[j - 1] > base) {
 96             nums[j] = nums[j - 1];
 97             j--;
 98         }
 99         nums[j] = base;
100 
101 #else
102         int j = i;
103         while(nums[j] < nums[j - 1]) { //减少一次判断（j > l)
104             swap(nums[j], nums[j - 1]);
105             --j;
106         }
107 #endif
108     }
109     return;
110 }
111 
112 //heapSort
113 void make_heap(vector<int> &nums, int father, int end) {
114     int son;
115     while((son = 2 * father + 1) < end) {
116         if(son + 1 < end && nums[son + 1] > nums[son]) ++son;
117         if(nums[father] >= nums[son]) return;
118         swap(nums[father], nums[son]);
119         father = son;
120     }
121     return;
122 }
123 
124 void heapSort(vector<int> &nums, int l, int r) { //O(n * lgn)
125     //heap 从第一非叶子节点开始初始化;
126     for(int i = r / 2 - 1; i >= l; --i) make_heap(nums, i, r);
127 
128     for(int i = r - 1; i > 0;) {
129         swap(nums[0], nums[i]);
130         make_heap(nums, 0, i--);
131     }
132     return;
133 }

Select/Bubble/Insert/Heap Sort

2. 快排(QuickSort) 及各种优化:

  1 //#include "sort.h"
  2 #include <iostream>
  3 #include <vector>
  4 #include <algorithm>
  5 using namespace std;
  6 
  7 #define MAX_N 1000
  8 
  9 #ifdef DEBUG
 10 #define logmsg(frm, args...) printf(frm, ##args);
 11 #else
 12 #define logmsg(frm, args...)  1;
 13 #endif
 14 
 15 #define TEST_FUNC(func, arg, a...) vector<int> arg(nums);\
 16     start = clock();\
 17     func(arg, ##a);\
 18     elapseTime = (double (clock() - start)) / CLOCKS_PER_SEC;\
 19     printf("after %s, time is %f\n", #func, elapseTime);\
 20     for(auto x : arg)  len += logmsg("%4d", x);\
 21     logmsg("\n");
 22 
 23 void swap(int &a, int &b) {
 24     int t = a;
 25     a = b;
 26     b = t;
 27     return;
 28 }
 29 
 30 void selectionSort(vector<int> &nums, int l, int r) {
 31     while(l < r) {
 32         int min_idx = l, max_idx = r - 1;
 33         //必须要下面一行，以防最值在下面两步swap 中被移动了;
 34         if(nums[min_idx] > nums[max_idx]) swap(nums[min_idx], nums[max_idx]);
 35         for(int i = l; i < r; ++i) {
 36             if(nums[i] < nums[min_idx]) min_idx = i;
 37             if(nums[i] > nums[max_idx]) max_idx = i;
 38         }
 39         swap(nums[l], nums[min_idx]);
 40         swap(nums[r - 1], nums[max_idx]);
 41         l++;
 42         r--;
 43     }
 44     return;
 45 }
 46 
 47 
 48 //排序 从小到大, 区间 左闭右开
 49 void bubbleSort(vector<int> &nums, int l, int r) {  //O(n * n)
 50     for(int i = r - 1; i > l; --i) {
 51         bool sortedFlag = true;  //优化： 一旦某次遍历没有任何交换，意味着所有数字都已经有序了；
 52         for(int j = l; j < i; ++j) {
 53             if(nums[j] > nums[j + 1]) {
 54                 swap(nums[j], nums[j + 1]);
 55                 sortedFlag = false;
 56             }
 57         }
 58         if(sortedFlag) return;
 59     }
 60     return;
 61 }
 62 
 63 //insert sort 在小数量数据，并且基本排序完成的 时间复杂度较好，极限(已经排序好的数组）可以到O(n) 比较即可
 64 void insertSort(vector<int> &nums, int l, int r) { // O(n) ~ O(n * n);
 65     for(int i = l + 1; i < r; ++i) {
 66 //way2:减少swap 次数
 67 #ifndef WAY1
 68         int base = nums[i], j = i;
 69         while(j > l && nums[j - 1] > base){
 70             nums[j] = nums[j - 1];
 71             j--;
 72         }
 73         nums[j] = base;
 74 
 75 #else
 76 //way1:
 77         for(int j = i; j > l; --j) {
 78             if(nums[j] >= nums[j - 1]) break;
 79             swap(nums[j], nums[j - 1]);
 80         }
 81 #endif
 82     }
 83     return;
 84 }
 85 
 86 void unguardedInsertSort(vector<int> &nums, int l, int r) {
 87     int min_idx = l;
 88     for(int i = l + 1; i < r; ++i) if(nums[i] < nums[min_idx]) min_idx = i;
 89     while(min_idx > l) {
 90         swap(nums[min_idx], nums[min_idx - 1]);
 91         --min_idx;
 92     }
 93     for(int i = l + 2; i < r; ++i) {
 94 #ifndef WAY1
 95         int base = nums[i], j = i;
 96         while(nums[j - 1] > base) {
 97             nums[j] = nums[j - 1];
 98             j--;
 99         }
100         nums[j] = base;
101 
102 #else
103         int j = i;
104         while(nums[j] < nums[j - 1]) { //减少一次判断（j > l)
105             swap(nums[j], nums[j - 1]);
106             --j;
107         }
108 #endif
109     }
110     return;
111 }
112 
113 //heapSort
114 void make_heap(vector<int> &nums, int father, int end) {
115     int son;
116     while((son = 2 * father + 1) < end) {
117         if(son + 1 < end && nums[son + 1] > nums[son]) ++son;
118         if(nums[father] >= nums[son]) return;
119         swap(nums[father], nums[son]);
120         father = son;
121     }
122     return;
123 }
124 
125 void heapSort(vector<int> &nums, int l, int r) { //O(n * lgn)
126     //heap 从第一非叶子节点开始初始化;
127     for(int i = r / 2 - 1; i >= l; --i) make_heap(nums, i, r);
128 
129     for(int i = r - 1; i > 0;) {
130         swap(nums[0], nums[i]);
131         make_heap(nums, 0, i--);
132     }
133     return;
134 }
135 
136 
137 int partition(vector<int> &nums, int l, int r) {
138     int base = nums[l], ret = l;
139     for(int i = l + 1; i < r; ++i) {
140         if(nums[i] < base) swap(nums[i], nums[++ret]);
141     }
142     swap(nums[l], nums[ret]);
143     return ret;
144 }
145 
146 //相比下面quickSort_pivot，这里递归只对左边；
147 void quickSort_single(vector<int> &nums, int l, int r) {
148     while(l < r) {
149         int pivot = partition(nums, l, r);
150         quickSort_single(nums, l, pivot);
151         l = pivot + 1;
152     }
153     return;
154 }
155 
156 void quickSort_pivot(vector<int> &nums, int l, int r) {
157     if(l >= r) return;
158 //way2: 找到小的往左边放;
159 #ifndef WAY1
160     int pivot = partition(nums, l, r);
161     quickSort_pivot(nums, l, pivot);
162     quickSort_pivot(nums, pivot + 1, r); // 对于递归，如果每次递归不能保证一定有区间的变化(pivot = l)，则有可能变成无限循环
163 #else
164 //左闭右开, 左边是未处理过，右边是处理过的数据,重合时候必然是右边被处理过的数据, 还可以不用判断 == 条件
165 //way1:  左边大的往右边放
166     int base = nums[l]; // 选定基准值
167     int l_shift = l + 1, r_shift = r;
168     while(l_shift < r_shift) {
169         if(nums[l_shift] < base) ++l_shift;
170         else swap(nums[l_shift], nums[--r_shift]);
171     }
172     //重合必然是右边的数据;
173     swap(nums[l], nums[--l_shift]);
174 
175     quickSort_pivot(nums, l, l_shift);  //base 对应位置已经确定了，所以不用在计入判断；
176                                         //所以树高相当于lg(n) ～ n (极限退化为n, 类似冒泡排序);
177                                         //整个复杂度为 O(n * log n) ~ O(n * n);
178     quickSort_pivot(nums, r_shift, r);
179 #endif
180     return;
181 }
182 
183 
184 const int threshold = 16;
185 
186 //三点取中值
187 int getMid(vector<int> &nums, int a, int b, int c) {
188     if(nums[a] > nums[b]) swap(a, b);
189     if(nums[a] > nums[c]) swap(a, c);
190     if(nums[b] > nums[c]) swap(b, c);
191     return b;
192 }
193 
194 int __unguarded_partition(vector<int> &nums, int base, int l, int r) {
195     while(l < r) {
196         while(nums[l] < base) l++;
197         r--;
198         while(nums[r] > base)  r--;  //不使用>= 判断条件是为了保证当数组中存在大量相等的数值，导致左右树极度不平衡
199         if(l < r) swap(nums[l++], nums[r]);
200     }
201     return l;
202 }
203 
204 void __quickSort(vector<int> &nums, int depth, int l, int r) {
205     while((r - l) > threshold) {
206         if(depth == 0)  {
207             heapSort(nums, l, r);
208             return;
209         }
210         depth--;
211 
212         int base = getMid(nums, l, r - 1, (l + (r - l) >> 1));
213 
214         //这里将mid 转换到l,保证 后面一定有值 >= base, 不会导致下面 __unguarded_partition 返回值越界
215         swap(nums[l], nums[base]);
216         base = nums[l];
217 
218         int __cnt = __unguarded_partition(nums, base, l + 1, r);
219         __quickSort(nums, depth, __cnt, r);
220         r = __cnt;
221     }
222     return;
223 }
224 
225 void quickSort_STL(vector<int> &nums, int l, int r) {
226     __quickSort(nums, __lg(r - l) * 2, l, r);
227     unguardedInsertSort(nums, l, r);
228     return;
229 }
230 
231 
232 int main()
233 {
234     int n = 0, len = 0;
235     scanf("%d", &n);
236     srand(time(0));
237     vector<int> nums;
238     clock_t start;
239     double elapseTime;
240     while(n--) nums.push_back(random() % MAX_N);
241 
242     for(auto x : nums)  len += printf("%8d", x);
243     printf("\n");
244     while(len--) printf("-");
245     printf("\n");
246 
247     TEST_FUNC(bubbleSort, b_nums, 0, nums.size());
248     TEST_FUNC(selectionSort, ss_nums, 0, nums.size());
249     TEST_FUNC(insertSort, i_nums,  0, nums.size());
250     TEST_FUNC(unguardedInsertSort, ui_nums, 0, nums.size());
251     TEST_FUNC(heapSort, hs_nums, 0, nums.size());
252     TEST_FUNC(quickSort_pivot, qs_nums, 0, nums.size());
253     TEST_FUNC(quickSort_single, qss_nums, 0, nums.size());
254     TEST_FUNC(quickSort_STL, qss2_nums, 0, nums.size());
255 
256 
257     start = clock();
258     sort(nums.begin(), nums.end(), greater<int>());
259     elapseTime = (clock() - start ) / CLOCKS_PER_SEC;
260     printf("std_sort time is %f\n", elapseTime);
261 
262 
263     return 0;
264 }

AllSortCode

STL 中sort 方法中使用的优化方法：初始混合排序(quickSort + heap Sort) + 后期 insertSort;

1). 单边递归（减少递归中栈空间深度）；

2). unguarded partition方法

3). base 取值采用三点取中法

4). 后期大部分数都已经在基本在正确位置，小规模数据，停止快排，使用插入排序；因为此时数组已经趋于有序，除非是整个逆序排序；

但是按照上面优化方式，速度还是没有STL 中sort快(与iterator 使用有关系？）

3. 归并排序(MergeSort) ; 其中核心思想在于先处理左边问题，再处理右边问题，最后处理横跨左右两边的信息；尽量将大的问题分解为几个小问题，通过堆小问题的处理，最终解决大的问题；分治思想；

　　如果对于一些问题，要求左边元素与右边元素有先后关系，那这类问题，天生就适合使用归并来处理；

 1 #include <iostream>
 2 #include <vector>
 3 
 4 #ifdef DEBUG 
 5     #define log(frm, arg...) printf(frm, ##arg);
 6 #else
 7     #define log(frm, arg...)
 8 #endif
 9 #define MAX_VAL 10000
10 using namespace std;
11 
12 void merge_sort(vector<int> &arr, int l, int r) {
13     if( l >= r ) return;
14     int mid = (l + r) >> 1;
15     merge_sort( arr, l, mid);
16     merge_sort( arr, mid + 1, r);
17 
18     int *temp = (int *) malloc(sizeof(int) * (r - l + 1));
19     int k = 0, p1 = l, p2 = mid + 1;
20     while( p1 <= mid || p2 <= r) {
21         if((p2 > r) || (p1 <= mid && arr[p1] <= arr[p2])) temp[k++] = arr[p1++];
22         else temp[k++] = arr[p2++];
23     }
24 
25     for( int i = l; i <=r; i++) arr[i] = temp[i-l];
26     free(temp);
27     return ;
28 }
29 
30 
31 int main()
32 {
33     int n;
34     scanf("%d", &n);
35     vector<int> arr;
36     srand(time(0));
37     for(int i = 0; i < n; i++) arr.push_back(rand() % MAX_VAL);
38 
39     log("%s\n", "before sort");
40     for(int i = 0; i < n; i++) {
41         log("%d ", arr[i]);
42     }
43 
44     merge_sort(arr, 0, n - 1);
45 
46     log("%s\n", "\nafter sort");
47     for(int i = 0; i < n; i++) {
48         log("%d ", arr[i]);
49     }
50     log("\n");
51     return 0;
52 }

MergeSort

上面code sample 中使用二路归并，其他还有三路，四路... 等多路归并，还有变路归并(在不同的递归层中，使用不同路归并); 对于多路排序中，可以直接使用优先队列寻找最值；

　　归并过程中，可以 从前合并，也可以从后面合并，核心在于按照顺序去处理已经有序的答案，实现有序；

　　思路不要局限，可以看这题：面试题 10.01. 合并排序的数组

 1 class Solution {
 2 public:
 3     void merge(vector<int>& A, int m, vector<int>& B, int n) {
 4         for(int i = m - 1, j = n - 1, end = m + n - 1; i >= 0 || j >= 0;) {
 5             if(j < 0 || (i >= 0 && A[i] >= B[j]))  A[end] = A[i--];
 6             else A[end] = B[j--];
 7             end--;
 8             if(end == i) return;
 9         }
10         return;
11     }
12 };

MergeSort(从后面进行归并）

4. 其他一些有意思的排序思想：

　　计数排序： 简单的单值排序问题，排序问题中数据的值域很有限；如统计14亿人的年龄，这样时间复杂度O(n)(人数+ 年龄范围）; 但是对于统计少量跨度极大的数据，则很不划算，如统计世界前100 首富与随机100人的财富，数据跨度很大，导致时间复杂度，财富范围远大于 n * n;

　典型题目：数据跨度有限　1122. 数组的相对排序

 1 class Solution {
 2 public:
 3     vector<int> relativeSortArray(vector<int>& arr1, vector<int>& arr2) {
 4         vector<int> cnt(1001, 0);
 5         for(auto &x : arr1) cnt[x] += 1;
 6         int ind = 0;
 7         for(auto &x : arr2) {
 8             while(cnt[x]--) arr1[ind++] = x;
 9             cnt[x] = 0;
10         }
11 
12         for(int i = 0; i <= 1000; i++) {
13             while(cnt[i]--) arr1[ind++] = i;
14         }
15 
16         return arr1;
17     }
18 };

计数排序

　　基数排序(RadixSort)：核心在于利用了数据的稳定性，某些情况下时间复杂度可以到O(n),比如最大数字为有限的位数。这里位数不局限于十进制，可以以0xFFFF 为第一位，0xFFFF0000 为第二位，只是计数空间会大点（空间换时间）;

　　借用到计数排序统计某位(个位/十位/百位...)中的数值个数，及计数结果的前缀和(代表各个计数数据的尾坐标)；然后将各个数值按照对应的尾坐标位置排列；

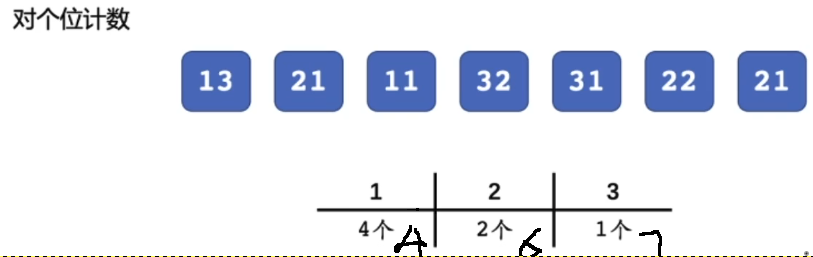
　　基于个位数字，排序结束以后数字顺序如下；然后基于十位数字计数结果，以及当前数字位置，将各个数按顺序放入由尾坐标对应的各个位置上。

 1 #include <iostream>
 2 #include <vector>
 3 #include <algorithm>
 4 using namespace std;
 5 
 6 #define BASE 0xFFFF
 7 #define LOWBIT(x) (x & BASE)
 8 #define __HIGHBIT(x) ((x >> 16) & BASE)
 9 
10 #define HIGHBIT(x) ((__HIGHBIT(x) > 0x7FFF) ? (__HIGHBIT(x) - 0x8000) : (__HIGHBIT(x) + 0x8000))
11 #ifdef DEBUG
12 #define LOG(frm, args ...) printf(frm, ##args)
13 #else 
14 #define LOG(frm, args ...) 
15 #endif
16 void radix_sort(vector<int> &nums) {
17     vector<int> cnt(BASE + 1, 0), temp(nums.size(), 0);
18 
19     for(auto &x : nums) cnt[LOWBIT(x)] += 1;
20     for(int i = 1; i <= BASE; ++i) cnt[i] += cnt[i - 1];
21     for(int i = nums.size() - 1; i >= 0; i--) temp[--cnt[LOWBIT(nums[i])]] = nums[i];
22 
23     for(auto &x : cnt) x = 0;
24 
25     for(auto &x : temp) cnt[HIGHBIT(x)] += 1;
26     for(int i = 1; i <= BASE; ++i) cnt[i] += cnt[i - 1];
27     for(int i = temp.size() - 1; i >= 0; --i) nums[--cnt[HIGHBIT(temp[i])]] = temp[i];
28 
29     return;
30 }
31 
32 void generateNums(vector<int>& nums) {
33     srand(time(0));
34     for(auto &x : nums) x = (random() % 2 ? -1 : 1) * (random() % (0xFFFFFFFF));
35     return;
36 }
37 
38 
39 int main()
40 {
41     int n = 0;
42     scanf("%d", &n);
43     vector<int> nums(n, 0), CMP(n, 0);
44 
45     generateNums(nums);
46     std::copy(nums.begin(), nums.end(), CMP.begin());
47     for(auto &x : nums) {
48         n += LOG("%10d,", x);
49     }
50     LOG("\n");
51     radix_sort(nums);
52     while(n--) LOG("-");
53     LOG("\nAfter Sort\n");
54     for(auto &x  : nums) {
55         LOG("%10d,", x);
56     }
57     LOG("\n");
58 
59     sort(CMP.begin(), CMP.end());
60     for(auto &x  : CMP) {
61         LOG("%10d,", x);
62     }
63     LOG("\n");
64 
65     return 0;
66 }

RadixSort

note: 如果将数组替换成map，看似减少空间以及遍历次数，但实际结果却并不快；hash 公式以及 map 的遍历会更加费时间...

具体差异如下面leetcode164解答;

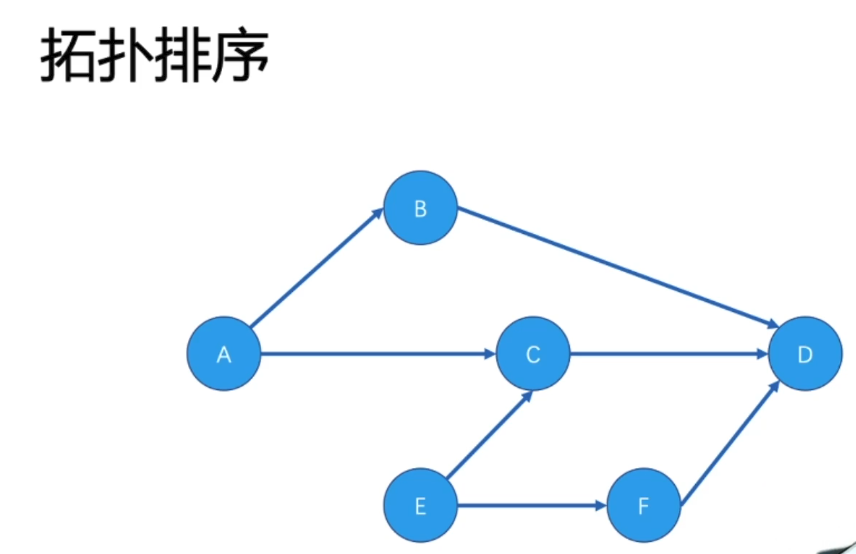
5. 拓扑排序：很多图论中排序都会涉及到拓扑排序，在实际应用中要学会抽象出问题核心进行建模；

　　比如下题可以对应的具体问题场景：某些点(C) 必须要有2 个来源才为真,有些点可以直接为真，有些点(B)有一个来源为真，有些永远不会为真(D); 那么针对这些点，寻找其中一种可能的传播顺序；（对各个点初始不同入度值，在入度值未耗尽前，不会进入下一个节点);

　　还可以对应为：选修课程，某些课程必须有前置课程需要（207. 课程表 & 210. 课程表 II）；

======================= **经典问题** =======================

//快排（partition 思想）

1. 只要求分布在某一范围内的数值，对于这些数值没有排序要求； leetcode17.14

　　直观的做法就是用堆来做，这里是应用了partition 的思路；

 1 class Solution {
 2 public:
 3 
 4     int getMid(int l, int m, int r) {
 5         if(l > r) swap(l, r);
 6         if(l > m) swap(l, m);
 7         if(m > r) swap(m ,r);
 8         return  m;
 9     }
10 
11     void _QS(vector<int> &arr, int head, int end) {
12         if(head >= end) return;
13 
14         int l = head, r = end, mid = getMid(arr[l], arr[(l + r) >> 1], arr[r]);
15         while(l < r) {
16             while(arr[l] < mid) l++;
17             while(arr[r] > mid) r--;
18             if(l <= r) swap(arr[l++], arr[r--]);
19         }
20         _QS(arr, head, r);
21         _QS(arr, l, end);
22         return;
23     }
24     
25     void partition(vector<int> &nums, int l, int r, int k) {
26         if(l >= r) return;
27         int x = l, y = r, base = getMid(nums[l], nums[r - 1], nums[(r + l) >> 1]);
28 
29         while(x < y) {
30             while(nums[x] < base) x++;
31             y--;
32             while(nums[y] > base) y--;
33             if(x < y) swap(nums[x++], nums[y]);
34         }
35 
36         int now = x - l;
37 
38         if(now == k) return;
39         else if(now < k) partition(nums, x, r, k - now);
40         else partition(nums, l, x, k);
41         return;
42     }
43 
44     vector<int> smallestK(vector<int>& arr, int k) {
45 //        _QS(arr, 0, arr.size() - 1);
46         partition(arr, 0, arr.size(), k);
47         return vector<int>(arr.begin(),arr.begin()+ k);
48     }
49 };

17.14

2. 二叉树的完全性验证 leetcode958 ：这题天然适合队列，不过也可以通过partition 方式来验证；

　　其中涉及完全二叉树中几个数值与编程技巧：假定root 对应树高为 1, 那么对于每个完全层对应的节点数 2^{depth - 1} ，从root 到当前完全层对应的节点总数为 2^depth- 1;

　　完全二叉数种最后一层中，左右子树中对应的节点个数，只有两种情况，左子树节点完全左子树节点不完全；所以最下面一层中，左子树对应的节点数为 min(total_cnt - (2^{depth - 1} - 1), 2 ^{depth - 2});

　　//这里还有一个关于数值边界条件注意，对于一定 >= 0 的范围，式子中包含 (2^{depth - 1} - 1)，自然就要有考虑到 -1 的可能性的习惯

 1 /**
 2  * Definition for a binary tree node.
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 8  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 9  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
10  * };
11  */
12 class Solution {
13 public:
14     int getCnt(TreeNode *root, int &cnt) {
15         if(!root) return 0;
16         cnt += 1;
17         return max(getCnt(root->left, cnt) , getCnt(root->right, cnt)) + 1;
18     }
19 
20     bool judge(TreeNode *root, int cnt, int depth_cnt) {
21         if(!root) return cnt == 0;
22         if(cnt == 0) return false;
23 
24         int left = min(cnt - (depth_cnt - 1), depth_cnt / 2) +  max(depth_cnt / 2 - 1, 0),
25             right = cnt - left - 1;
26 
27         return judge(root->left, left, depth_cnt / 2) && judge(root->right, right, depth_cnt / 2);
28     }
29 
30 
31     bool isCompleteTree(TreeNode* root) {
32         int cnt = 0, depth = 0;
33         depth = getCnt(root, cnt); //depth 从1 开始;
34         if(depth > 7) return false;  //不超过100 个节点
35 
36         int depth_cnt = pow(2, depth - 1);
37 
38         return  judge(root, cnt, depth_cnt);
39 
40 
41 
42 //        queue<TreeNode *> que;
43 //        que.push(root);
44 //        bool null_cut = false;
45 //        while(que.size()) {
46 //            for(int i = 0, I = que.size(); i < I; ++i) {
47 //                TreeNode *temp = que.front();
48 //                que.pop();
49 //                if(temp->left) {
50 //                    if(null_cut) return false;
51 //                    que.push(temp->left);
52 //                } else null_cnt = true;
53 //                if(temp->right) {
54 //                    if(null_cut) return false;
55 //                    que.push(temp->right);
56 //                } else null_cut = true;
57 //            }
58 //        }
59 //        return true;
60     }
61 };

二叉树完全性验证

//归并：

3. 合并K个升序链表 (leetcode23) :比较典型的归并思想题目，还有对于多个数值比较时候，常用堆来实现；

 1 /**
 2  * Definition for singly-linked list.
 3  * struct ListNode {
 4  *     int val;
 5  *     ListNode *next;
 6  *     ListNode() : val(0), next(nullptr) {}
 7  *     ListNode(int x) : val(x), next(nullptr) {}
 8  *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 9  * };
10  */
11 class Solution {
12 public:
13     struct CMP {
14         bool operator() (ListNode* a, ListNode* b) {
15             return a->val > b->val;
16         }
17     };
18     ListNode* mergeKLists(vector<ListNode*>& lists) {
19         ListNode head, *pre = &head;
20         priority_queue<ListNode*, vector<ListNode*>,  CMP> pq;
21         for(auto &x : lists) if(x) pq.push(x);
22 
23         while(pq.size()) {
24             pre->next = pq.top();
25             pre = pre->next;
26             pq.pop();
27             if(pre->next) pq.push(pre->next);
28         }
29         return head.next;
30     }
31 };

归并/堆

4.基本版： 315. 计算右侧小于当前元素的个数 (leetcode315) :

 1 class Solution {
 2 public:
 3     vector<int> temp;
 4     void getCnt(vector<int>& nums, vector<int> &index, vector<int> &cnt, int l, int r) {
 5         if(l >= r) return;
 6         int mid = (l + r) >> 1,
 7             p1 = l, p2 = mid + 1, ind = l;
 8         getCnt(nums, index, cnt, l, mid);
 9         getCnt(nums, index, cnt, mid + 1, r);
10 
11         while(p1 <= mid || p2 <= r) {
12             if(p1 > mid || (p2 <= r && nums[index[p2]] >= nums[index[p1]])) temp[ind++] = index[p2++];
13             else {
14                 if(p2 <= r) cnt[index[p1]] += (r - p2 + 1);
15                 temp[ind++] = index[p1++];
16             }
17         }
18 
19         std::copy(temp.begin() + l, temp.begin() + r + 1, index.begin() + l);
20         return;
21     }
22 
23     vector<int> countSmaller(vector<int>& nums) {
24         vector<int> ans(nums.size(), 0), index(nums.size(), 1);
25         index[0] = 0;
26         std::partial_sum(index.begin(), index.end(), index.begin());
27         while(temp.size() < index.size()) temp.push_back(0);
28         getCnt(nums, index, ans, 0, nums.size() - 1);
29         return ans;
30     }
31 };

前缀和/分治

　　进阶版，求区间：区间和的个数(leetcode327) : 将大问题分解为小问题，然后求解小问题；

 1 class Solution {
 2 public:
 3     vector<long long> temp;
 4     int countTwoPart(vector<long long> &ps, int l1, int r1, int l2, int r2, int lower, int upper) {
 5         int ans = 0, k1 = l1, k2 = l1;
 6         for(int j = l2; j <= r2; ++j) {
 7             long long j_low = ps[j] - upper,
 8                  j_upper = ps[j] - lower;
 9             while(k1 <= r1 && ps[k1] < j_low) k1++;
10             while(k2 <= r1 && ps[k2] <= j_upper) k2++;
11             ans += (k2 - k1);
12         }
13         return ans;
14     }
15 
16     int getCnt(vector<long long>& ps, int l, int r, int lower, int upper) {
17         if(l >= r) return 0;
18 
19         int mid = (l + r) >> 1, 
20         ret = getCnt(ps, l, mid, lower, upper) + getCnt(ps, mid + 1, r, lower, upper),
21         lp = l, rp = l,  // 左边满足条件的下标
22         l_ind = l, r_ind = mid + 1, ind = l; //merge 中下标
23 
24 //使用这个单独函数时间会少很多，但是下面将这个过程放在下面不是可以减少循环次数？这里时间和cpu命中有关系？
25 //        ret += countTwoPart(ps, l, mid, mid + 1, r, lower, upper);
26 
27         while(l_ind <= mid || r_ind <= r) {
28             if(r_ind > r|| (l_ind <= mid && ps[l_ind] <= ps[r_ind])) {
29                 temp[ind++] = ps[l_ind++];
30             } else {
31                 long long i_low = ps[r_ind] - upper, i_upper = ps[r_ind] - lower;
32                 while(lp <= mid && ps[lp] < i_low) lp++;
33                 rp = lp;
34                 while(rp <= mid && ps[rp] <= i_upper) rp++;
35                 ret += (rp - lp);
36                 temp[ind++] = ps[r_ind++];
37             }
38         }
39         std::copy(temp.begin() + l, temp.begin() + r + 1, ps.begin() + l);
40         return ret;
41     }
42 
43     int countRangeSum(vector<int>& nums, int lower, int upper) {
44         int len = nums.size();
45         vector<long long> pSum(len + 1);
46         temp.push_back(0);
47         for(int i = 0; i < len; ++i) {
48             pSum[i + 1] = pSum[i] + nums[i];
49             temp.push_back(0);
50         }
51 //        std::partial_sum(nums.begin(), nums.end(), pSum.begin());
52 
53         return getCnt(pSum, 0, len, lower, upper);
54     }
55 };

前缀和/分治

5. 多路归并： 1508. 子数组和排序后的区间和

 1 class Solution {
 2 public:
 3 #define MOD_NUM (long long)(1e9 + 7)
 4     struct Data{
 5         Data(int i, int j, int sum) : i(i), j(j), sum(sum){}
 6         int i, j, sum;
 7     };
 8     struct CMP{
 9         bool operator()(const Data &a, const Data&b) {
10             return a.sum > b.sum;
11         }
12     };
13     
14     int rangeSum(vector<int>& nums, int n, int left, int right) {
15         long long ans = 0;
16         priority_queue<Data, vector<Data>, CMP> pq;
17         for(int i = 0; i < n; ++i) pq.push(Data(i, i, nums[i]));
18 
19         for(int i = 1; i <= right; ++i) {
20             Data temp = pq.top();
21             pq.pop();
22             if(temp.j + 1 < n) pq.push(Data(temp.i, temp.j + 1, temp.sum + nums[temp.j + 1]));
23             if(i < left) continue;
24             ans =(ans + temp.sum) % MOD_NUM;
25         }
26 
27         return ans;
28     }
29 #undef MOD_NUM
30 };

多路归并

//计数与基数等排序方式：

6. 164. 最大间距：针对题目要求，使用线性空间，以及线性时间复杂度：

 1 class Solution {
 2 public:
 3 #define BASE 0xFFFF
 4 #define LOWBIT(X)  (X & BASE)
 5 #define HIGHBIT(X) ((X >> 16) & BASE)
 6     
 7     int maximumGap(vector<int>& nums) {
 8 //计数排序
 9 //正常计数思路
10 //        map<int,int> cnt;
11 //        int ans = 0, pre = -1;
12 //        for(auto &x : nums) cnt[x] += 1;
13 //        for(auto &x : cnt) {
14 //            if( -1 == pre) pre = x.first;
15 //            ans = max(ans, x.first - pre);
16 //            pre = x.first;
17 //        }
18 //针对题意优化
19 //        set<int> num(nums.begin(), nums.end());
20 //        int ans = 0;
21 //        for(auto iter = num.begin(); next(iter) != num.end(); iter++) ans = max(ans, (*next(iter) - *iter));
22 //        return ans;
23 
24 //Radix_Sort
25 //使用STL map, 看似减少空间及遍历次数，但是实际消耗时间更长; 只能说hasp 公式更费时间；
26 //        int cnt_sum = 0, len = nums.size();
27 //        map<int, int> cnt, ind;
28 //        vector<int> temp(len, 0);
29 //
30 //        for(auto &x : nums) cnt[LOWBIT(x)] += 1;
31 //        for(auto &x : cnt) ind[x.first] = (cnt_sum += x.second);
32 //        for(int i = len - 1; i >= 0; --i) temp[--ind[LOWBIT(nums[i])]] = nums[i];
33 //
34 //        cnt.clear();
35 //        ind.clear();
36 //        cnt_sum = 0;
37 //
38 //        for(auto &x : temp) cnt[HIGHBIT(x)] += 1;
39 //        for(auto &x : cnt) ind[x.first] = (cnt_sum += x.second);
40 //        for(int i = len - 1; i >= 0; --i) nums[--ind[HIGHBIT(temp[i])]] = temp[i];
41 //
42 //        cnt_sum = 0;
43 //        for(int i = 1; i < len; ++i) cnt_sum = max(cnt_sum, (nums[i] - nums[i - 1]));
44 //        return cnt_sum;
45         int cnt[BASE + 1] = {0};
46         vector<int> temp(nums.size(), 0);
47         for(auto &x : nums) cnt[LOWBIT(x)] += 1;
48         for(int i = 1; i <= BASE; ++i) cnt[i] += cnt[i - 1];
49         for(int i = nums.size() - 1; i >= 0; --i) temp[--cnt[LOWBIT(nums[i])]] = nums[i];
50 
51         memset(cnt, 0, sizeof(cnt));
52         for(auto &x : temp) cnt[HIGHBIT(x)] += 1;
53         for(int i = 1; i <= BASE; ++i) cnt[i] += cnt[i - 1];
54         for(int i = temp.size() - 1; i >= 0; --i) nums[--cnt[HIGHBIT(temp[i])]] = temp[i];
55         int ans = 0;
56         for(int i = 1, I = nums.size(); i < I; ++i) ans = max(ans, nums[i] - nums[i -1]);
57         return ans;
58 
59 //STL sort
60 //        sort(nums.begin(), nums.end());
61 //        int ans = 0;
62 //        for(int i = 1, I = nums.size(); i < I; ++i) ans = max(ans, nums[i] - nums[i - 1]);
63 //        return ans;
64 
65     }
66 #undef BASE
67 #undef LOWBIT
68 #undef HIGHBIT
69 };

计数/基数/STL sort

//拓扑排序：

7. 207. 课程表 & 210. 课程表 II ：通过不断将有依赖的课程中减去（通过入度-1 操作）无依赖（入度为0）的课程；最终查看是否所有课程都入度为0；

 1 class Solution {
 2 public:
 3     bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
 4         vector<int> indeg(numCourses, 0);
 5         vector<vector<int>> toNext(numCourses);
 6         queue<int> finishCourse;
 7 
 8         for(auto &x : prerequisites) {
 9             indeg[x[0]] += 1;
10             toNext[x[1]].push_back(x[0]);
11         }
12 
13         for(int i = 0; i < numCourses; i++) {
14             if(indeg[i]) continue;
15             finishCourse.push(i);
16         }
17 
18         while(finishCourse.size()) {
19             int cur = finishCourse.front();
20             finishCourse.pop();
21             numCourses -= 1;
22             for(auto &x : toNext[cur]) {
23                 indeg[x] -= 1;
24                 if(!indeg[x]) finishCourse.push(x);
25             }
26         }
27 
28         return !numCourses;
29     }
30 };

207

 1 class Solution {
 2 public:
 3     vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
 4         vector<int> indeg(numCourses, 0);
 5         vector<vector<int>> toNext(numCourses);
 6         queue<int> finishCourse;
 7         vector<int> ans;
 8 
 9         for(auto &x : prerequisites) {
10             indeg[x[0]] += 1;
11             toNext[x[1]].push_back(x[0]);
12         }
13 
14         for(int i = 0; i < numCourses; i++) {
15             if(indeg[i]) continue;
16             finishCourse.push(i);
17         }
18 
19         while(finishCourse.size()) {
20             int cur = finishCourse.front();
21             finishCourse.pop();
22             ans.push_back(cur);
23             for(auto &x : toNext[cur]) {
24                 indeg[x] -= 1;
25                 if(!indeg[x]) finishCourse.push(x);
26             }
27         }
28         if(ans.size() < numCourses) return vector<int>();
29         return ans;
30     }
31 };

210

======================= **应用场景** =======================

1. 归并排序：大数据排序是霸主级排序方式；

　　　　　　大数据排序时，可以将排序的结果不断的放在外存中（因为只需要不断的在文件后写入数据），然后在内存中只需要存储这几个部分的对应指针就可以进行上一层排序；

posted on 2022-01-17 22:57 学海一扁舟阅读(67) 评论(0) 编辑收藏举报

刷新页面返回顶部