堆(heap) & 优先队列(priority_queue)

======================= **基础知识** =======================

1. 应用 完全二叉树 结构，通过连续数组空间储存( 左子树：2 * n,  右子树 ： 2 * n + 1; root = 1) ， 实现一个完全二叉树;

　　要学会 数组（表现形式） 与 完全二叉树 （思维结构）之间的转换！

　　数据结构：本质就是定义一种性质，并在所有操作中都要维护这种性质的；

　　　　　　　　　　   也就意味这数据结构中包含 数据定义 + 结构操作(增删改查）两部分，对于这段的理解，结合下面 2& 3 部分仔细理解；

 

2.  任意 三元组中，顶点节点 是最大节点： 大顶堆；下一大节点，在第一大节点下一层; 下下大节点，是在下一层或下下一层中；所以兄弟节点之间大小没有直接关系；

　　　　　　　　   顶点节点 是最小节点： 小顶堆； 同样性质类似大顶堆;

 

3.  增操作，结尾插入新元素， 然后将堆进行满足性质的位置调整（上浮调整）；

　  删操作，弹出堆定元素，然后将数组中最后一个元素调整到堆顶（保证是完全二叉树），然后做弹出后为满足性质的位置调整（下沉调整）；

 

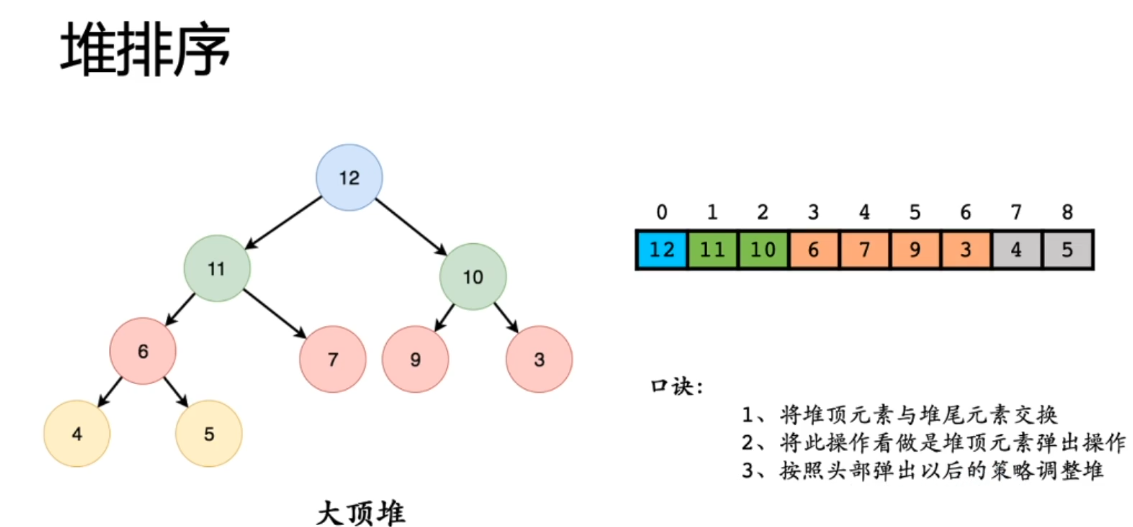
4. 堆排序（如下图）：

参考下面示意图：使用大顶堆，然后每次将弹出的最大值放到数组末尾，弹出所有元素以后，数组的值就是从小到排序！

 

5. 堆 为什么 又叫优先队列?

　比较下面的性质，会发现下面很多类似的地方；所以堆是优先队列的实现方式；

普通队列	优先队列
尾部入队	尾部插入数据
头部出队	头部弹出数据
先进先出(FIFO)	每次出队权值(最大/小元素)
数组实现	数组实现，逻辑上是一个堆

 

======================= **代码演示** =======================

1. 实现一个大顶堆(顺带实现堆排序);

//#include "heap.h"
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;

//定义大顶堆

struct my_heap{
#define MAX_N 1000
    int h[MAX_N + 5], len;
    my_heap(): len(0) {
        memset(h, 0, sizeof(int) * (MAX_N + 5));
    }
    bool empty(){
        return len == 0;
    }

    int size() {
        return len;
    }

    int top() {
        if(empty()) return -1;
        return h[0];
    }
    void push(int val) {
        int next = (len - 1) / 2, cur =  len;
        h[len++] = val;
        while(cur && h[next] < h[cur]) {
            swap(h[next], h[cur]);
            cur = next;
            next = (cur - 1) / 2;
        }
        return ;
    }

    void pop() {
        if(empty()) return;
        swap(h[0], h[--len]);
        int cur = 0, next = 2 * cur + 1;
        while(next < len){
            if(next + 1 < len && h[next] < h[next + 1]) next += 1;
            if(h[cur] > h[next]) break;
            swap(h[cur], h[next]);
            cur = next;
            next = 2 * cur + 1;
        }
        return;
    }

    void output(int cnt) {
        cout << "now heap: " ;
        for(int i = 0; i < cnt; ++i) cout << h[i] << " ";
        cout << endl;
        return;
    }

};


int main()
{
    my_heap h1;
    int op, val, max_cnt = 0;
    cout << "Pls input op & val.\n 0: stop;\n 1: push;\n 2: pop;\n 3: size;\n 4: output;\n" << endl;
    while(cin >> op) {
        if(!op) break; // 0: stop;
        switch (op) {
            case 1: {  //push
                         cin >> val;
                         h1.push(val);
                         cout << "after push ," ;
                         max_cnt = max(max_cnt, h1.size());
                         h1.output(h1.size());
                    } break;
            case 2: {
                        h1.pop();
                        cout << "after pop ,";
                        h1.output(h1.size());
                    } break;
            case 3: cout << h1.size() << endl; break;
            case 4: h1.output(h1.size()); break;
            default : cout << "error op code\n";
        }
    }

    cout << "the seq:" ;
    h1.output(max_cnt);  //输出一个升序数组，必须是先都push, 后面都pop
    return 0;
}

 下面用C++ 实现heap， 泛型编程，继承，STL, 仿函数，const；

C++ 中有很多实现了的方法，这些方法 怎样在实际工作复用，并针对异常等处理， 存在很多细节...

#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>

using namespace std;

template<typename T>
class heap_cpp : public vector<T> {
    private:
        function<bool(T, T)> cmp;
        int _size;
    public:
        template<typename Func_T>
        heap_cpp(Func_T fn) : cmp(fn), _size(0){}
        bool empty() {
            return this->empty();
        }
        int size() const{
            return _size;
        }
        T top() const{
            return this->at(0);
        }
        void push(T t){
            this->push_back(t);
            push_heap(this->begin(), this->end(), cmp);
            _size += 1;
            return;
        }
        void pop() {
            pop_heap(this->begin(), this->end(), cmp);
            this->pop_back();
            _size -= 1;
            return;
        }
};

template<typename T>
void output(T t1) {
    for(auto &x : t1) cout << x << " ";
    cout << endl;
}

int main()
{
    heap_cpp<int> h1{less<int>()};
    int val;
    while(cin >> val) {
        h1.push(val);
        cout << "after push :";
        output(h1);
    }

    while(h1.size()) {
        cout << h1.top() << endl;
        h1.pop();
    }

    return 0;
}

======================= **经典问题** =======================

堆适合维护： 集合最值！！

(所以针对一个数组，要不断取得其中最值，用堆来处理这个数组);

1. 最小/大 的k个数(leetcode:offer40)

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {
        priority_queue<int,vector<int>, greater<int>> pq;
        for(auto x : arr) pq.push(x);
        vector<int> ans;
        while(k--) {
            ans.push_back(pq.top());
            pq.pop();
        }
        return ans;
    }
};

2. 数据流中第K 大元素：(leetcode703) 

　　 数据不断变化中，然后要求第K 大值，要不断对新增加数据排序，所以堆最优；

　　(set/multiset 也可以实现排序，但是指定位置值返回不方便，更适合寻找特定的值是否存在；vector 等线性结构不具备排序功能，每次都要重新排序，费时）；

　　固定数组的话，直接排序，然后求值即可;(leetcode215)

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end(), greater<int>());
        return nums[k - 1];
    }
};

3. 查找和最小的K 对数字(leetcode373): 这里有个比较有意思的点，求的是小的值，实现的却是大顶堆(限制k个数);

　　　　通过超出就有目的性的删除或跳出循环，来实现最小k 组；这也是heap 数据结构自身的特性决定的；

　　　　set 这里也可以用来取代heap；

class Solution {
public:

    template<typename T>
    class heap : public vector<T> {
        public:

            template<typename Func_T>
            heap(Func_T fun):cmp(fun){}
            T& top() { return this->at(0);} 
            void pop(){
                pop_heap(this->begin(),this->end(),cmp);
                this->pop_back();
                return ;
            }
            void push(const T& a){
                this->push_back(a);
                push_heap(this->begin(),this->end(),cmp);
                return ;
            }

        private:
            function<bool(T,T)> cmp;

    };

    struct CMP {
        bool operator()(vector<int> a, vector<int> b){
            return a[0]+a[1] < b[0]+b[1] ;
        }
    };
    vector<vector<int>> kSmallestPairs(vector<int>& nums1, vector<int>& nums2, int k) {
        CMP less_than;
        heap<vector<int>> h{less_than};
        vector<int> temp(2) ;
        for (auto i : nums1) {
            for(auto j : nums2) {
                temp[0] = i, temp[1] = j;
                if (h.size() < k || less_than(temp,h.top())) {
                    h.push(temp);
                    if (h.size() > k) h.pop();
                } else {
                    break;
                }
            }
        }
        return h;
    }
};

4. 数据流中的中位数 (leetcode295)

class MedianFinder {
public:
    priority_queue<int, vector<int>, less<int>> front;
    priority_queue<int, vector<int>, greater<int>> back;

    MedianFinder(){}
    
    void addNum(int num) {
        if(front.size() == 0 || num <= front.top()) front.push(num);
        else back.push(num);

        if(back.size() > front.size()) {
            int temp = back.top();
            back.pop();
            front.push(temp);
        }
        if(front.size() > back.size() + 1) {
            int temp = front.top();
            front.pop();
            back.push(temp);
        }

        return;
    }
    
    double findMedian() {
        int len = front.size() + back.size();
        if(len % 2) return front.top();
        return (double(front.top() + back.top()) / 2.0);
    }
};

/**
 * Your MedianFinder object will be instantiated and called as such:
 * MedianFinder* obj = new MedianFinder();
 * obj->addNum(num);
 * double param_2 = obj->findMedian();
 */

5.  丑数(leetcode264) : 这题解法中包含了Euler 素数筛概念，每一个合数必定由 最小质数 * 最大因子 ，因此对于每一个合数，都可以由最小素因子标定；

至于这里的heap，则是用来决定顺序的；

(如果能找到某个数对应的具体位置(没找到算法），也可以用二分来找）;

class Solution {
public:
    int nthUglyNumber(int n) {
        priority_queue<long long, vector<long long>, greater<long long>> pq;
        int factor[3] = {2, 3, 5};
        pq.push(1);
        while(--n) {
            long long temp = pq.top();
            pq.pop();
            for(int i = 0; i < 3; ++i) {
                pq.push(temp * factor[i]);
                if(0 == temp % factor[i]) break;
            }
        }
        return pq.top();
    }
};

 

======================= **应用场景** =======================

基本 前K 个大/小的值问题,

　　不断变化(插入/删除) 的数组，寻找一个某个有序情况下的值， 大都适合heap 来处理