======================= **基础知识** =======================
1. 树形结构: 从代码结构来看,Tree 与 链表类似,主要在指针域的区别; 链表可以看成一叉树;
树形结构中: 节点代表集合,边代表关系 (RB tree/ trie...), 比如说 左边是小于关系,所以左边拎出来都是小于根节点的集合; 右边是大于关系,右边拎出来都是大于根节点的集合;细节还要后面更多数据结构体会;

1 typedef struct Node { 2 int data; 3 struct Node *next; 4 5 }Node, *LinkedList; 6 7 8 typedef struct Node { 9 int data; 10 struct Node *next[3]; 11 12 }Node, *Tree;
2. 二叉树: (图论中有出度 与 入度差别), tree 中说的度是节点中有几个子孩子;
a: 每个节点度最多为2;
b: 度为0 的节点比度为2 的节点多一个;(n 个节点的树有 n - 1 边,n0 + n1 + n2 = n1 + 2 * n2 + 1 --> n2 = n0 - 1;)
3. 二叉树遍历:基本用递归/迭代方式实现;
a: 遍历方式: 前序遍历(根, 左, 右);中序遍历(左, 根, 右);后续遍历(左,右, 根);还有层序遍历;
b: 还原一个二叉树(中序遍历 + 前序(后序) 遍历 就可以还原一个二叉树); leetcode105

1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode() : val(0), left(nullptr), right(nullptr) {} 8 * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 9 * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} 10 * }; 11 */ 12 class Solution { 13 public: 14 TreeNode *generateList(vector<int>& preorder, int s1, int e1, 15 vector<int>& inorder, int s2, int e2) { 16 if(s1 == e1) return nullptr; 17 int val = preorder[s1], idx2 = s2; 18 while(inorder[idx2] != val) idx2 += 1; 19 int l2 = idx2 - s2, r2 = e2 - idx2; 20 21 TreeNode *n = new TreeNode(val); 22 n->left = generateList(preorder, s1 + 1, s1 + 1 + l2, inorder, s2, idx2); 23 n->right = generateList(preorder, s1 + 1 + l2, e1, inorder, idx2 + 1, e2); 24 return n; 25 } 26 27 TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) { 28 return generateList(preorder, 0, preorder.size(), inorder, 0, inorder.size()); 29 } 30 };
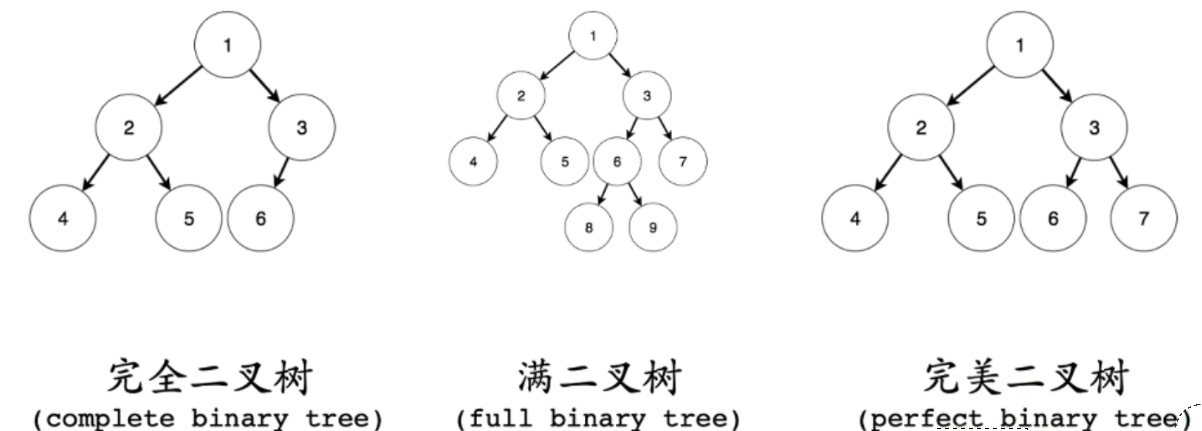
4. 完全二叉树(堆/优先队列 : 维护集合最值):在最后一层尾部缺少节点的二叉树;
a: 实现时候可以用连续储存空间,不通过指针域方式来得到子结点位置(左孩子: 2 * i , 右孩子: 2 * i + 1);
b: 计算式方式 与 记录式 相互转换实现方式;
c: 因为可以通过数组方式实现,所以一个数组,既可以是一组数字,也可以是一个完全二叉树结构;
相同的数据,在不同结构的体现出来的思维方式不同;
满二叉树: 只有度为0 与 度2 节点;
完美二叉树: 所有层级中节点都是全的;
5. 多叉树/森林:(字典树Trie / AC 自动机 : 字符串查找及其相关转换问题; 并查集 : 连同性问题)
6. 二叉排序树(AVL tree/ RB tree / 2-3 树: STL中数据结构中数据检索容器的底层实现方式)
7. B树/B+ 树(多叉平衡树): 文件系统/数据库 底层重要数据结构;
======================= **代码演示** =======================
1. 随即插入节点,实现二叉树, 然后以前序遍历 与 中序遍历 打印出来;
代码小技巧:在random_insert 函数中,返回节点值,并被上一层函数接住;树中经常能看到类似的做法,递归或回溯中也会有可能用到;

1 #include <iostream> 2 using namespace std; 3 4 typedef struct Node{ 5 int key; 6 struct Node *lchild, *rchild; 7 } Node; 8 9 Node* getNewNode(int key){ 10 Node *p = (Node*) malloc(sizeof(Node)); 11 p->key = key; 12 p->lchild = NULL; 13 p->rchild = NULL; 14 return p; 15 } 16 17 Node *random_insert(Node *root, int key){ 18 if (root == NULL) return getNewNode(key); 19 if (rand()%2){ 20 root->lchild = random_insert(root->lchild,key); 21 } else { 22 root->rchild = random_insert(root->rchild,key); 23 } 24 return root; 25 } 26 27 void pre_order(Node *root){ 28 if(root == NULL) return; 29 cout<<root->key<<" "; 30 pre_order(root->lchild); 31 pre_order(root->rchild); 32 return ; 33 } 34 35 void in_order(Node *root){ 36 if(root == NULL) return; 37 pre_order(root->lchild); 38 cout<<root->key<<" "; 39 pre_order(root->rchild); 40 return ; 41 } 42 43 int main(int argc, char* argv[]) 44 { 45 srand(time(0)); 46 if( argc != 2) return 0; 47 int MAX_N = atoi(argv[1]); 48 Node *root = NULL; 49 for (int i = 1; i <= MAX_N; i++){ 50 root = random_insert(root,i); 51 } 52 pre_order(root); 53 cout<<endl; 54 in_order(root); 55 cout<<endl; 56 57 return 0; 58 }
======================= **经典问题** =======================
1. 前/中/后序遍历:(leetcode589) 递归/迭代都可以

1 /* 2 // Definition for a Node. 3 class Node { 4 public: 5 int val; 6 vector<Node*> children; 7 8 Node() {} 9 10 Node(int _val) { 11 val = _val; 12 } 13 14 Node(int _val, vector<Node*> _children) { 15 val = _val; 16 children = _children; 17 } 18 }; 19 */ 20 21 class Solution { 22 public: 23 void _preorder(Node* _root, vector<int>& _ans) { 24 if(_root == nullptr) return ; 25 _ans.push_back(_root->val); 26 for(auto i: _root->children) { 27 _preorder(i,_ans); 28 } 29 return ; 30 } 31 vector<int> preorder(Node* root) { 32 vector<int> ans; 33 // _preorder(root, ans); 34 if(!root) return ans; 35 36 stack<Node*> s1; 37 s1.push(root); 38 stack<int> idx; 39 idx.push(0); 40 ans.push_back(root->val); 41 while(s1.size()) { 42 Node* temp = s1.top(); 43 int index = idx.top(); 44 if((temp->children).size() <= index) { 45 s1.pop(); 46 idx.pop(); 47 continue; 48 } 49 idx.pop(); 50 idx.push(index + 1); 51 Node *n_temp = temp->children[index]; 52 ans.push_back(n_temp->val); 53 s1.push(n_temp); 54 idx.push(0); 55 } 56 57 return ans; 58 } 59 };
平衡二叉树判断(leetcode110) : 这题有意思的点是递归函数意义的定义,递归函数中意义定义是关键!

1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode() : val(0), left(nullptr), right(nullptr) {} 8 * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 9 * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} 10 * }; 11 */ 12 class Solution { 13 public: 14 int getDeepth(TreeNode* root) { 15 if(!root) return 0; 16 int left = getDeepth(root->left); 17 int right = getDeepth(root->right); 18 if(left < 0 || right < 0 || abs(left - right) > 1) return -2; 19 return max(left, right) + 1; 20 } 21 bool isBalanced(TreeNode* root) { 22 return (getDeepth(root) >= 0); 23 } 24 };
2. 二叉树层序遍历: leetcode_offer32 ,基本大部分树结构的问题都可以通过递归来实现;

1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 void getResult(TreeNode *r, int level, vector<vector<int>> &ret) { 13 if(r == nullptr) return; 14 if(ret.size() < level) ret.push_back(vector<int>(1, r->val)); 15 else ret[level - 1].push_back(r->val); 16 getResult(r->left, level + 1, ret); 17 getResult(r->right, level + 1, ret); 18 return; 19 } 20 vector<vector<int>> levelOrder(TreeNode* root) { 21 vector<vector<int>> ans; 22 getResult(root, 1, ans); 23 return ans; 24 } 25 };
另外deque 结构天生就适合树的层序遍历(leetcode662);

1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode() : val(0), left(nullptr), right(nullptr) {} 8 * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} 9 * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} 10 * }; 11 */ 12 class Solution { 13 public: 14 int widthOfBinaryTree(TreeNode* root) { 15 if(!root) return 0; 16 17 typedef pair<TreeNode*, int> PTI; 18 deque<PTI> dq; 19 int ans = 0, start = 0; 20 21 dq.push_back(make_pair(root, 0)); 22 while(dq.size()) { 23 int cnt = dq.size(); 24 ans = max(ans, dq.back().second - dq.front().second + 1); 25 start = dq.front().second; 26 for(int i = 0; i < cnt; ++i) { 27 PTI temp = dq.front(); 28 dq.pop_front(); 29 if(temp.first->left) dq.push_back(make_pair(temp.first->left, (temp.second - start) * 2)); 30 if(temp.first->right) dq.push_back(make_pair(temp.first->right, (temp.second - start) * 2 + 1)); 31 } 32 } 33 return ans; 34 } 35 };
3. 241. 为运算表达式设计优先级 : 二叉树结构 也适合处理 计算式 的优先级类型,优先级最低的是根节点;

1 class Solution { 2 public: 3 void processStr(string s, vector<int> &num, vector<char> &op) { 4 int val = 0; 5 for(int i = 0; s[i]; ++i) { 6 if(s[i] >= '0' && s[i] <= '9') { 7 val = val * 10 + (s[i] - '0'); 8 continue; 9 } 10 num.push_back(val); 11 val = 0; 12 op.push_back(s[i]); 13 } 14 num.push_back(val); 15 return; 16 } 17 18 vector<int> getAns(vector<int> &nums, vector<char> &op, int l, int r) { 19 if(l == r) return vector<int>{nums[l]}; 20 vector<int> ans; 21 for(int i = l; i < r; i++) { 22 vector<int> left = getAns(nums, op, l, i), 23 right = getAns(nums, op, i + 1, r); 24 for(auto &x: left) { 25 for(auto &y: right) { 26 int val = 0; 27 switch (op[i]) { 28 case '+' : ans.push_back(x + y); break; 29 case '-' : ans.push_back(x - y); break; 30 case '*' : ans.push_back(x * y); break; 31 } 32 } 33 } 34 } 35 return ans; 36 } 37 38 vector<int> diffWaysToCompute(string expression) { 39 vector<int> nums, ans; 40 vector<char> op; 41 processStr(expression, nums, op); 42 43 return getAns(nums, op, 0, op.size()); 44 45 } 46 };
======================= **应用场景** =======================
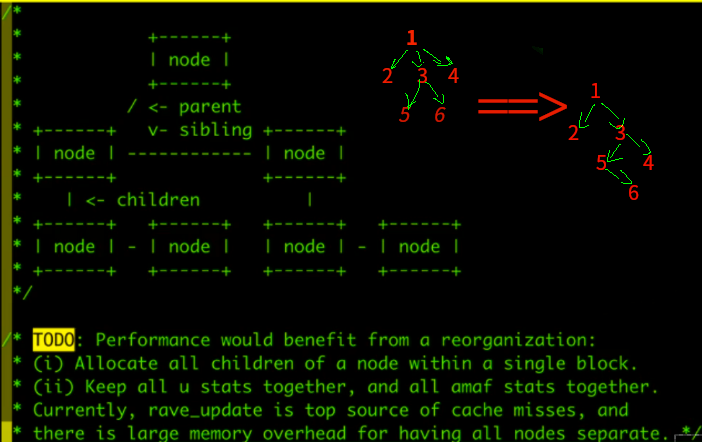
1. 左孩子 右兄弟表示法节省空间: AlphaGo 中实现棋盘数据存储;
多叉树中,并不是每一个节点都能将所有的指针域用起来,此时如果用多叉树结果,每个节点都会占用相当的内存空间;所以用左孩子,右兄弟表示方法可以有效减少指针域中所占用的空间;不过这样操作有可能增加树高哦!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号