======================= 基础知识 =======================
一段连续存储区存储任意数据,包含head,tail(最后一个元素的下一位:因为一般都是采用前开后闭区间,这样 cnt = tail - head);
支持操作有push(队尾入队),pop(队首出队);
先入先出(FIFO);
队列出队,入队多次操作以后,如果没有重复利用先前出队的空间,而队尾空间已经用完,会导致假溢出(队列前有未用空间,但是队尾已经无法插入了),所以可以使用 循环队列 实现重复利用前段空间。如果所有空间都被用了,那就是真溢出了,此时需要动态扩容(有可能用块状链表,hash 链表等方式实现,具体语言实现可能不同,可扩展)
表现形式可以是数组,链表(环形链表,从头出队,从尾入队);
======================= 代码演示 =======================
//循环队列:

1 class Queue { 2 public : 3 Queue(int n = 10) : arr(n), head(0), tail(0), cnt(0) {} 4 5 int size() { return cnt;} 6 bool empty() { return cnt == 0;} 7 bool full() { return cnt == arr.size();} 8 9 void push(int x) { 10 if (full()) { 11 cout << "queue full" << endl; 12 return ; 13 } 14 arr[tail++] = x; 15 tail %= arr.size(); 16 cnt += 1; 17 return ; 18 } 19 void pop(){ 20 if (empty()) return ; 21 cnt -= 1; 22 head = ++head % arr.size(); 23 return ; 24 } 25 int front() { 26 if (empty()) return 0; 27 return arr[head]; 28 } 29 void clear() { 30 head = tail = cnt = 0; 31 return ; 32 } 33 void output() { 34 cout << "Queue : "; 35 for (int i = 0, j = head; i < cnt; i++) { 36 cout << arr[j] << " "; 37 j += 1; 38 if (j == arr.size()) j = 0; 39 } 40 cout << endl; 41 return ; 42 } 43 44 private: 45 int head, tail; 46 int cnt; 47 vector<int> arr; 48 };

1 class MyCircularDeque { 2 private : 3 int size; 4 int front; 5 int tail; 6 int *p; 7 8 public: 9 MyCircularDeque(int k):size(k), front(0), tail(0) { 10 p = (int *) malloc(sizeof(int) * k); 11 } 12 13 bool insertFront(int value) { 14 if(isFull()) return false; 15 front = (front - 1 + size) % size; 16 *(p + front) = value; 17 len += 1; 18 return true; 19 } 20 21 bool insertLast(int value) { 22 if(isFull()) return false; 23 *(p + tail) = value; 24 len += 1; 25 tail = (tail + 1) % size; 26 return true; 27 } 28 29 bool deleteFront() { 30 if(isEmpty()) return false; 31 front = (front + 1) % size; 32 len -= 1; 33 return true; 34 } 35 36 bool deleteLast() { 37 if(isEmpty()) return false; 38 tail = (tail - 1 + size) % size; 39 len -= 1; 40 return true; 41 } 42 43 int getFront() { 44 if(isEmpty()) return -1; 45 return *(p + front); 46 } 47 48 int getRear() { 49 if(isEmpty()) return -1; 50 return *(p + (tail - 1 + size) % size); 51 } 52 53 bool isEmpty() { 54 return len == 0; 55 } 56 57 bool isFull() { 58 return len == size; 59 } 60 };
======================= 经典问题 =======================
1. 设计前中后队列(leetcode1670): 这题目很好的诠释了,复杂的结构 如何通过简单数据结构来 实现:

1 class FrontMiddleBackQueue { 2 private: 3 class DEQUE{ 4 private: 5 class Node { 6 public: 7 Node *pre; 8 Node *next; 9 int val; 10 Node(int v, Node *p = nullptr, Node *n = nullptr) : val(v), pre(p), next(n){}; 11 }; 12 13 int _size; 14 Node *front; 15 Node *back; 16 public: 17 bool isEmpty(){ 18 return _size == 0; 19 } 20 int size(){ 21 return _size; 22 } 23 DEQUE(): _size(0){ 24 front = new Node(0); 25 back = new Node(0); 26 front->next = back; 27 back->pre = front; 28 } 29 ~DEQUE() { 30 while(front) { 31 Node *temp = front; 32 front = front->next; 33 delete temp; 34 } 35 } 36 void insertFront(int val){ 37 Node *temp = new Node(val); 38 temp->next = front->next; 39 front->next = temp; 40 temp->pre = temp->next->pre; 41 temp->next->pre = temp; 42 _size += 1; 43 return; 44 } 45 int popFront(){ 46 if(isEmpty()) return -1; 47 Node* temp = front->next; 48 int val = temp->val; 49 front->next = temp->next; 50 temp->next->pre = temp->pre; 51 _size -= 1; 52 delete temp; 53 return val; 54 } 55 void insertBack(int val){ 56 Node *temp = new Node(val); 57 58 temp->pre = back->pre; 59 temp->next = temp->pre->next; 60 back->pre = temp; 61 temp->pre->next = temp; 62 63 _size += 1; 64 return; 65 } 66 int popBack(){ 67 if(isEmpty()) return -1; 68 Node *temp = back->pre; 69 int val = temp->val; 70 71 temp->pre->next = temp->next; 72 back->pre = temp->pre; 73 74 _size -= 1; 75 return val; 76 } 77 78 }; 79 DEQUE front, back; 80 int size; 81 public: 82 FrontMiddleBackQueue():size(0), front(DEQUE()), back(DEQUE()) {} 83 84 bool isEmpty() { 85 return size == 0; 86 } 87 88 void adjustFB(){ 89 if(front.size() > back.size()){ 90 int val = front.popBack(); 91 back.insertFront(val); 92 } 93 if(back.size() - front.size() > 1){ 94 int val = back.popFront(); 95 front.insertBack(val); 96 } 97 return; 98 } 99 100 void pushFront(int val) { 101 front.insertFront(val); 102 size += 1; 103 adjustFB(); 104 return; 105 } 106 107 void pushMiddle(int val) { 108 front.insertBack(val); 109 size += 1; 110 adjustFB(); 111 return; 112 } 113 114 void pushBack(int val) { 115 back.insertBack(val); 116 size += 1; 117 adjustFB(); 118 return; 119 } 120 121 int popFront() { 122 if(isEmpty()) return -1; 123 int ret; 124 if(size == 1) ret = back.popFront(); 125 else ret = front.popFront(); 126 size -= 1; 127 adjustFB(); 128 return ret; 129 } 130 131 int popMiddle() { 132 if(isEmpty()) return -1; 133 int ret; 134 if(size % 2) ret = back.popFront(); 135 else ret = front.popBack(); 136 size -= 1; 137 // adjustFB(); 138 return ret; 139 } 140 141 int popBack() { 142 if(isEmpty()) return -1; 143 int ret = back.popBack(); 144 size -= 1; 145 adjustFB(); 146 return ret; 147 } 148 }; 149 150 /** 151 * Your FrontMiddleBackQueue object will be instantiated and called as such: 152 * FrontMiddleBackQueue* obj = new FrontMiddleBackQueue(); 153 * obj->pushFront(val); 154 * obj->pushMiddle(val); 155 * obj->pushBack(val); 156 * int param_4 = obj->popFront(); 157 * int param_5 = obj->popMiddle(); 158 * int param_6 = obj->popBack(); 159 */
2. 灵活运用数据结构自身的性质,来实现一些要求(leetcode143)

1 /** 2 * Definition for singly-linked list. 3 * struct ListNode { 4 * int val; 5 * ListNode *next; 6 * ListNode() : val(0), next(nullptr) {} 7 * ListNode(int x) : val(x), next(nullptr) {} 8 * ListNode(int x, ListNode *next) : val(x), next(next) {} 9 * }; 10 */ 11 class Solution { 12 public: 13 void reorderList(ListNode* head) { 14 deque<ListNode*> dq; 15 ListNode *temp = head; 16 while(temp) { 17 dq.push_back(temp); 18 temp = temp->next; 19 } 20 21 temp = dq.front(); 22 dq.pop_front(); 23 while(dq.size() > 1) { 24 temp->next = dq.back(); 25 dq.pop_back(); 26 temp = temp->next; 27 28 temp->next = dq.front(); 29 dq.pop_front(); 30 temp = temp->next; 31 } 32 if(dq.size()) { 33 temp->next = dq.back(); 34 temp = temp->next; 35 } 36 37 temp->next = nullptr; 38 return; 39 } 40 };
======================= 应用场景 =======================
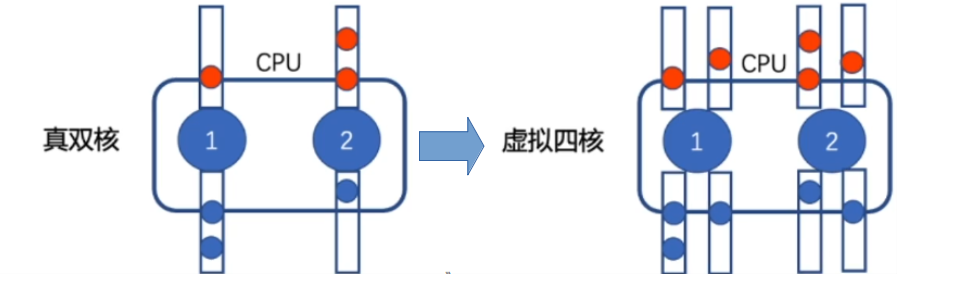
1. cpu 超线程技术(不同于系统的process & thread):利用cpu处理速度更快,增加每个核对应的 任务队列(并不一定越多越好,2个适宜);
(题外话:还有多路cpu(计算结点), 集群 概念)
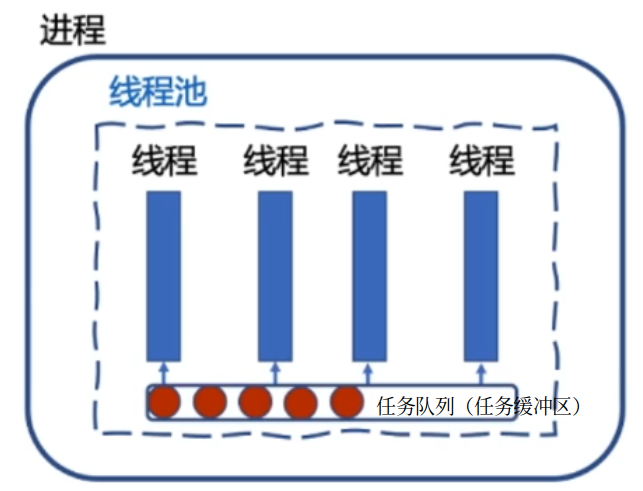
2. 线程池 的任务队列:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号