[ONTAK2010]Peaks(kruskal重构树+主席树)
题目描述
在Bytemountains有N座山峰,每座山峰有他的高度h_i。有些山峰之间有双向道路相连,共M条路径,每条路径有一个困难值,现在有Q组询问,每组询问询问从点v开始只经过困难值小于等于x的路径所能到达的山峰中第k高的山峰,如果无解输出-1。
思路
1.离线做法(启发式合并+第k大数据结构)
为了防止进行删除边的操作,我们先把询问按困难值x从小到大排序
用一个数据结构维护每一个连通块(开始时每个点为一个连通块),对于每一次加边,相当于合并两个连通块(可以使用并查集维护联通性质),合并的话直接将小的那个连通块一个点一个点的拆下来加进大的连通块就可以了
每加一个点的复杂度是(logn或者1)可以感性理解一下这样子做总共加点次数不超过nlogn,所以总复杂度就是O(\(nlog^2n\))或者O(\(nlogn\))
某数据结构可以是主席树或者平衡树什么的
Code:没有
2.在线做法(kruskal重构树+主席树)
如果两点之间已经有一条路径了,那么无论再加多少边也不会改变两点的连通性。换句话说,影响两点连通性的只是两点间的最短路径上的边。将这个性质代到n个点的图中,显然影响任意两点连通性的所有边形成了该图的最小生成树。
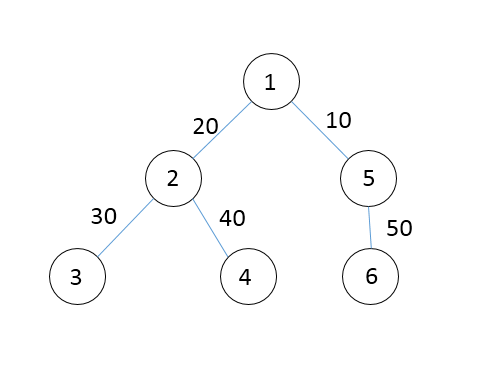
然后就可以使用重构树了。我们将n个点作为重构树的叶子节点,在kruskal求最小生成树的过程中,每得到一条树边,就将这条边用一个权值为边权的点表示,其儿子为原树边连接的两个点所分别对应的最上层的祖先节点,如下图所示。
最小生成树
对应的重构树(方节点表示边)
于是乎我们就把不能经过边的问题变成了不能经过点的问题
举个栗子,从1出发不超过40困难度能到达除了6之外的其他地方,而在下面的重构树中可以发现40这个节点所有的儿子节点即为可以到达的点。
所以我们对于从i出发不超过x困难度这个询问,从i出发向上跳,直到跳到根节点或者当前节点的父亲的权值大于x,记当前节点为j,要求第k大的数,就是在j这颗子树的叶子中找第k大。
So? 如果按照点加入的顺序对点进行了排列(比如上面的图中应该把5号点放在1和2之间,因为5比2先加入),就可以发现任意一个边节点所对应的子树的叶子节点都是连续的,我们只需要维护这个连续的区间的左右边界,那么问题就变成了经典的静态区间第k大问题,可以使用主席树来做。
Code:
#include<bits/stdc++.h>
#define N 100005
#define M 6000005
using namespace std;
int n,m,q,sum,rt,b[N],len;
int h[N<<1],fa[N],f[N<<1][20],top[N];
int seg[N],rev[N],minn[N<<1],maxx[N<<1],c;
int root[N],s[M],l[M],r[M],num;
bool vis[N<<1];
struct E { int u,v,dis; } e[N*10];
struct Edge
{
int next,to;
}edge[N*5];int head[N*2],cnt=1;
void add_edge(int from,int to)
{
edge[++cnt].next=head[from];
edge[cnt].to=to;
head[from]=cnt;
}
template <class T>
void read(T &x)
{
char c;int sign=1;
while((c=getchar())>'9'||c<'0') if(c=='-') sign=-1; x=c-48;
while((c=getchar())>='0'&&c<='9') x=(x<<1)+(x<<3)+c-48; x*=sign;
}
void ad(int x,int y,int d)
{
h[++sum]=d;
int lx=x,ly=y;
x=top[x];y=top[y];
f[x][0]=f[y][0]=sum;
top[lx]=top[ly]=sum;
}
bool cmp(E a,E b) {return a.dis<b.dis;}
int find(int x) {return fa[x]==x ? x : fa[x]=find(fa[x]);}
void kruskal()
{
for(int i=1;i<=n;++i) fa[i]=top[i]=i;
sort(e+1,e+m+1,cmp);
int cnt=0; sum=n;
for(int i=1;i<=m;++i)
{
int fu=find(e[i].u),fv=find(e[i].v);
if(fu!=fv)
{
fa[fu]=fv;
ad(fu,fv,e[i].dis);
if(++cnt==n-1) break;
}
}
}
void dfs1(int x)
{
if(vis[x]) return;
vis[x]=1;
if(f[x][0])
{
dfs1(f[x][0]);
add_edge(f[x][0],x);
}
else rt=x;
for(int i=1;i<=19;++i) f[x][i]=f[f[x][i-1]][i-1];
}
void dfs(int u)
{
minn[u]=n+1;maxx[u]=0;
if(u<=n)//叶子
{
seg[++c]=u;
rev[u]=c;
maxx[u]=minn[u]=c;
return;
}
for(int i=head[u];i;i=edge[i].next)
{
int v=edge[i].to;
if(v==f[u][0]) continue;
dfs(v);
maxx[u]=max(maxx[u],maxx[v]);
minn[u]=min(minn[u],minn[v]);
}
}
void build(int &rt,int L,int R)
{
rt=++num;
if(L==R) return;
int mid=(L+R)>>1;
build(l[rt],L,mid);
build(r[rt],mid+1,R);
}
int modify(int rt,int L,int R,int x,int v)
{
int t=++num;
l[t]=l[rt];r[t]=r[rt];s[t]=s[rt]+v;
if(L==R) return t;
int mid=(L+R)>>1;
if(x<=mid) l[t]=modify(l[rt],L,mid,x,v);
else r[t]=modify(r[rt],mid+1,R,x,v);
return t;
}
int query(int rt1,int rt2,int L,int R,int k)
{
if(L==R) return L;
int x=s[l[rt2]]-s[l[rt1]];
int mid=(L+R)>>1;
if(x>=k) return query(l[rt1],l[rt2],L,mid,k);
else return query(r[rt1],r[rt2],mid+1,R,k-x);
}
int main()
{
memset(h,-1,sizeof(h));
read(n);read(m);read(q);
for(int i=1;i<=n;++i) read(h[i]),b[++len]=h[i];
for(int i=1;i<=m;++i) read(e[i].u),read(e[i].v),read(e[i].dis);
kruskal();
for(int i=1;i<=n;++i) dfs1(i);
dfs(rt);
sort(b+1,b+len+1);
len=unique(b+1,b+len+1)-b-1;
build(root[0],1,len);
for(int i=1;i<=n;++i)
{
int x=seg[i];
int loc=lower_bound(b+1,b+len+1,h[x])-b;
root[i]=modify(root[i-1],1,len,loc,1);
}
while(q--)
{
int st,x,k;
read(st);read(x);read(k);
for(int i=19;i>=0;--i)
{
if(h[f[st][i]]<=x&&h[f[st][i]]!=-1) st=f[st][i];
}
if(maxx[st]-minn[st]+1<k) {printf("-1\n");continue;}
int rk=query(root[minn[st]-1],root[maxx[st]],1,len,maxx[st]-minn[st]+2-k);
printf("%d\n",b[rk]);
}
return 0;
}
介绍一道几乎一样的题 [HNOI2012]永无乡



 浙公网安备 33010602011771号
浙公网安备 33010602011771号