manacher算法
manacher算法是在O(n)的复杂度内求回文串长度的算法。
算法过程如下。
先在所有字符之间加上一种没有意义的字符。
比如“#”,“|”等。来去除偶数回文和奇数回文的区别。
再在第0位加上“~”,这样就可以保证不会出范围。
其中rb表示当前mid的回文串右边界。
枚举中间点 i 如果 i 在右边界之前。
p[i],也就是i时的回文半径。 j 为 i 关于mid的对称点。
关于mid的更新在下面再说。
p[ i ] = min( p[ j ] , rb-i );
这句话尝试用j的回文长度来求i的回文长度。
因为关于mid对称,所以p[i]可以等于p[j]。
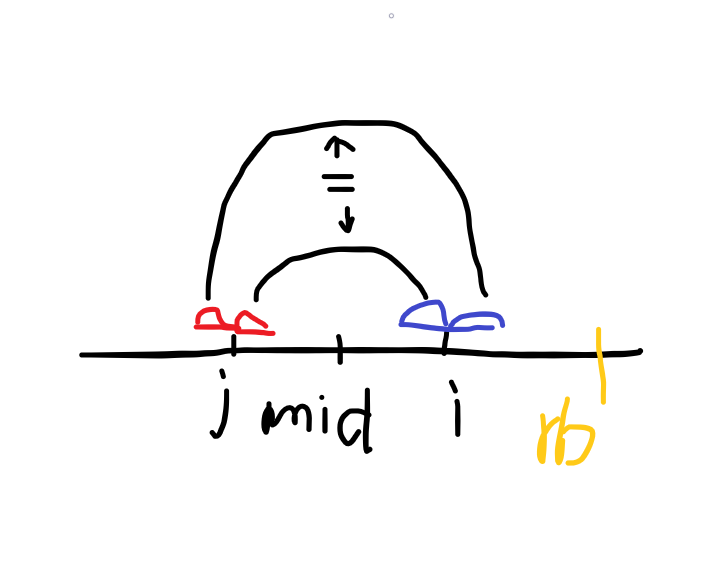
如果i在右边界之后,则p[i]=1;
那么就可以继续向后查。
while(da[i-p[i]]==da[i+p[i]])
p[i]++;
将半径扩大。
这时候如果p[i]+i大于rb,也就是现在的范围超出了原来的范围。
那么可以更新rb=p[i]+i; 那么 mid=i;
总体算法结束。
那么最后的答案,最长回文长度就是最长半径-1。(为什么减一?规律哈哈哈哈)
模板:https://www.luogu.org/problemnew/show/P3805
代码如下:
#include<bits/stdc++.h> using namespace std; const int maxn=11000001; char da[maxn<<1]; int p[maxn<<1],cnt=1; int rb,maxx,mid; int main() { char c=getchar(); da[0]='~'; da[1]='#'; while(c>'z'||c<'a') c=getchar(); while(c<='z'&&c>='a'){ da[++cnt]=c; da[++cnt]='#'; c=getchar(); } for(int i=1;i<=cnt;i++){ if(i<rb) p[i]=min(p[(mid<<1)-i],rb-i); else p[i]=1; while(da[i-p[i]]==da[i+p[i]]) p[i]++; if(p[i]+i>rb) rb=p[i]+i,mid=i; maxx=max(p[i],maxx); } printf("%d\n",maxx-1); // while(1); // system("pasue"); return 0; }

