记录相机成像原理二 （张正友标定）

由世界坐标系转换到像素坐标系的运算

 

 

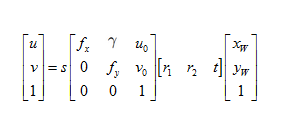
 其中，u、v表示像素坐标系中的坐标，s表示尺度因子，fx、fy、u0、v0、γ（由于制造误差产生的两个坐标轴偏斜参数，通常很小）表示5个相机内参，R,t表示相机外参，Xw、Yw、Zw（假设标定棋盘位于世界坐标系中Zw=0的平面）表示世界坐标系中的坐标。

 

其中从世界坐标系转换到像素坐标系可以称之为是单应性变换。首先学习单应性变换的推导过程，假设在齐次坐标系上，有点 [x, y, 1] 和 变换后的点 [x', y', 1]

单应性矩阵H定义为：

 

 

 

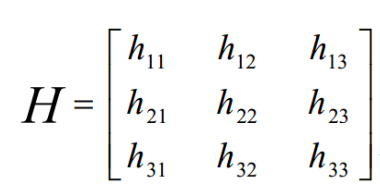
则有矩阵相乘：

 

 

 

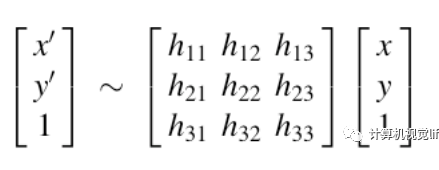
展开：

 

 

 

 

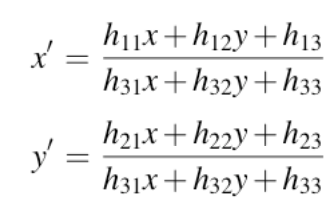
想求解矩阵，首先看其自由度，确定解的range，因为使用齐次坐标系，可以对其进行任意大小的缩放：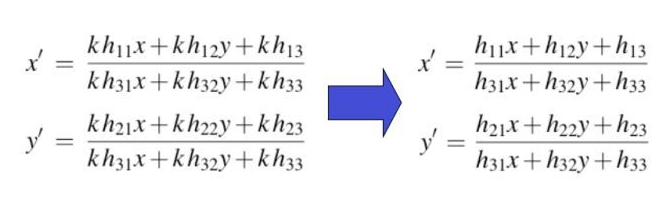

 

所以其free variable 是8

可以将其表示为如下的形式：让其模为1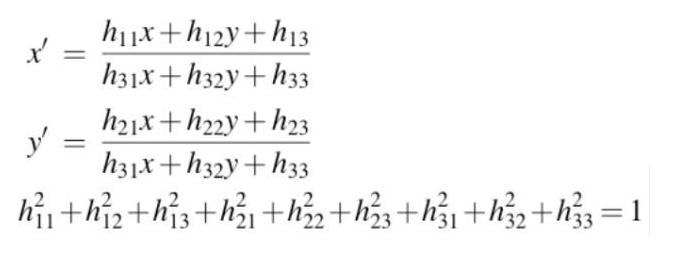

 

 

 展开整理：

 

 

 

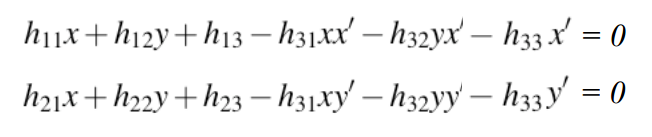
一对对应的点可以展开成：

 

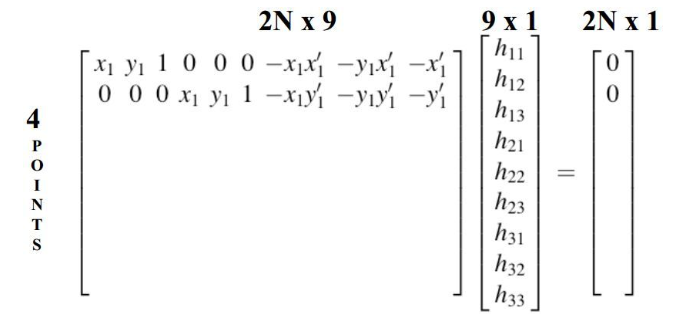
因此我们需要四组对应的点，才能求解，但是真实情况下，给出的点组是会有像素偏差的，所以在真实应用场景，会提供更多组的点来求出最优解

 

 

 在opencv中有现成的函数可以调用 cv::findHomography(...) => cv::Mat

 

求出单应性矩阵H后，要想办法将其拆分为相机的内参，外参矩阵