[BZOJ] 1798: [Ahoi2009]Seq 维护序列seq #线段树：区间加+区间乘+区间求和

1798: [Ahoi2009]Seq 维护序列seq

Time Limit: 30 Sec  Memory Limit: 64 MB
Submit: 7136  Solved: 2582
[Submit][Status][Discuss]

Description

老师交给小可可一个维护数列的任务，现在小可可希望你来帮他完成。 有长为N的数列，不妨设为a1,a2,…,aN 。有如下三种操作形式： (1)把数列中的一段数全部乘一个值; (2)把数列中的一段数全部加一个值; (3)询问数列中的一段数的和，由于答案可能很大，你只需输出这个数模P的值。

Input

第一行两个整数N和P(1≤P≤1000000000）。第二行含有N个非负整数,从左到右依次为a1,a2,…,aN, (0≤ai≤1000000000,1≤i≤N)。第三行有一个整数M，表示操作总数。从第四行开始每行描述一个操作，输入的操作有以下三种形式： 操作1：“1 t g c”(不含双引号)。表示把所有满足t≤i≤g的ai改为ai×c (1≤t≤g≤N,0≤c≤1000000000)。 操作2：“2 t g c”(不含双引号)。表示把所有满足t≤i≤g的ai改为ai+c (1≤t≤g≤N,0≤c≤1000000000)。 操作3：“3 t g”(不含双引号)。询问所有满足t≤i≤g的ai的和模P的值 (1≤t≤g≤N)。 同一行相邻两数之间用一个空格隔开，每行开头和末尾没有多余空格。

Output

对每个操作3，按照它在输入中出现的顺序，依次输出一行一个整数表示询问结果。

Sample Input

7 43
1 2 3 4 5 6 7
5
1 2 5 5
3 2 4
2 3 7 9
3 1 3
3 4 7

Sample Output

2
35
8

HINT

【样例说明】

初始时数列为(1,2,3,4,5,6,7)。
经过第1次操作后，数列为(1,10,15,20,25,6,7)。
对第2次操作，和为10+15+20=45，模43的结果是2。
经过第3次操作后，数列为(1,10,24,29,34,15,16}
对第4次操作，和为1+10+24=35，模43的结果是35。
对第5次操作，和为29+34+15+16=94,模43的结果是8。



测试数据规模如下表所示

数据编号 1 2 3 4 5 6 7 8 9 10
N= 10 1000 1000 10000 60000 70000 80000 90000 100000 100000
M= 10 1000 1000 10000 60000 70000 80000 90000 100000 100000

Source

Day1

Analysis

= =退役前最后一天补掉了，，，从学线段树那天开始就没有做出来的题

进步还是有的

唉

关于两种标记之间关系的处理可以通过这个例子来说明

　　

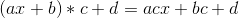
那么显然，在增加乘法标记的时候只需要把值和总和一同进行乘法计算就行了

如果没有加法标记的话就直接将乘法标记进行乘法计算

同时注意，在pushdown的时候需要优先计算乘法标记

还有一件事，记得开 long long，并且跟计算有关的变量都要long long = =

（没开在luogu只过了3个点= =）

Code

#include<stdio.h>
#include<iostream>
#define maxn 200005
#define mid (L+R)/2
#define lc (rt<<1)
#define rc (rt<<1|1)
#define LL long long
using namespace std;

int n,m; LL mod;

struct node{ LL sum,add_lazy,mul_lazy; }T[maxn*4];

int read(){
	int ret = 0,t = 1; char ctr = getchar();
	while(ctr < '0' || ctr > '9') (ctr == '-' && (t = -1)),ctr = getchar();
	while(ctr >= '0' && ctr <= '9') ret = ret*10+ctr-'0',ctr = getchar();
	return ret;
}

void maintain(int rt){ T[rt].sum = (T[lc].sum+T[rc].sum)%mod; }

void mul_single(int rt,LL val){
	T[rt].sum = T[rt].sum*val%mod;
	T[rt].mul_lazy = 1LL*T[rt].mul_lazy*val %mod;
	T[rt].add_lazy = 1LL*T[rt].add_lazy*val %mod;
}

void add_single(int rt,int L,int R,LL val){
	T[rt].sum = (T[rt].sum+val*(R-L+1))%mod;
	T[rt].add_lazy = (T[rt].add_lazy+val)%mod;
}

void pushdown(int rt,int L,int R){
	if(T[rt].mul_lazy != 1){
		mul_single(lc, T[rt].mul_lazy);
		mul_single(rc, T[rt].mul_lazy);
		T[rt].mul_lazy = 1;
	}
	
	if(T[rt].add_lazy){
		add_single(lc, L, mid, T[rt].add_lazy);
		add_single(rc, mid+1, R, T[rt].add_lazy);
		T[rt].add_lazy = 0;
	}
}

void build(int rt,int L,int R){
	T[rt].add_lazy = 0; T[rt].mul_lazy = 1;
	if(L == R) T[rt].sum = read();
	else{
		build(lc,L,mid); build(rc,mid+1,R);
		maintain(rt);
	}
}

void mul_modify(int rt,int L,int R,int qL,int qR,LL val){
	pushdown(rt,L,R);
	if(qL <= L && R <= qR) mul_single(rt,val);
	else{
		if(qL <= mid) mul_modify(lc, L, mid, qL, qR, val);
		if(qR > mid) mul_modify(rc, mid+1, R, qL, qR, val);
		maintain(rt);
	}
}

void add_modify(int rt, int L, int R, int qL,int qR,LL val){
	pushdown(rt,L,R);
	if(qL <= L && R <= qR) add_single(rt,L,R,val);
	else{
		if(qL <= mid) add_modify(lc,L,mid,qL,qR,val);
		if(qR > mid) add_modify(rc,mid+1,R,qL,qR,val);
		maintain(rt);
	}
}

LL query(int rt,int L,int R,int qL,int qR){
	pushdown(rt,L,R);
	if(qL <= L && R <= qR) return T[rt].sum;
	else{
		LL ret = 0;
		if(qL <= mid) ret += query(lc,L,mid,qL,qR);
		if(qR > mid) ret += query(rc,mid+1,R,qL,qR);
		return ret%mod;
	}
}

int main(){
	scanf("%d%lld",&n,&mod);
	build(1,1,n);
	scanf("%d",&m);
	
	for(int i = 1;i <= m;i++){
		int a,b,c; LL d; scanf("%d",&a);
		switch(a){
			case 1: //b = read(), c = read(), d = read();
				scanf("%d%d%lld",&b,&c,&d);
				mul_modify(1,1,n,b,c,d); break;
			case 2: //b = read(), c = read(), d = read();
				scanf("%d%d%lld",&b,&c,&d);
				add_modify(1,1,n,b,c,d); break;
			case 3: //b = read(), c = read();
				scanf("%d%d",&b,&c);
				printf("%lld\n",query(1,1,n,b,c)%mod);
		}
//		printf("Now: "); for(int j = 1;j <= n;j++) printf("%d ",query(1,1,n,j,j)); cout << endl;
	}
	
	
	return 0;
}