[UOJ] #261 天天爱跑步
#261. 天天爱跑步 NOIP2016 D1T2
题目描述
小C同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一棵包含 nn 个结点和 n−1n−1 条边的树,每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 11 到 nn 的连续正整数。
现在有 mm 个玩家,第 ii 个玩家的起点为 SiSi,终点为 TiTi。每天打卡任务开始时,所有玩家在第 00 秒同时从自己的起点出发,以每秒跑一条边的速度,不间断地沿着最短路径向着自己的终点跑去,跑到终点后该玩家就算完成了打卡任务。(由于地图是一棵树,所以每个人的路径是唯一的)
小C想知道游戏的活跃度,所以在每个结点上都放置了一个观察员。在结点 jj 的观察员会选择在第 WjWj 秒观察玩家,一个玩家能被这个观察员观察到当且仅当该玩家在第 WjWj 秒也正好到达了结点 jj。小C想知道每个观察员会观察到多少人?
注意:我们认为一个玩家到达自己的终点后该玩家就会结束游戏,他不能等待一段时间后再被观察员观察到。即对于把结点 jj 作为终点的玩家:若他在第 WjWj 秒前到达终点,则在结点 jj 的观察员不能观察到该玩家;若他正好在第 WjWj 秒到达终点,则在结点 jj 的观察员可以观察到这个玩家。
输入格式
从标准输入读入数据。
第一行有两个整数 nn 和 mm。其中 nn 代表树的结点数量,同时也是观察员的数量,mm 代表玩家的数量。
接下来 n−1n−1 行每行两个整数 uu 和 vv,表示结点 uu 到结点 vv 有一条边。
接下来一行 nn 个整数,其中第 jj 个整数为 WjWj,表示结点 jj 出现观察员的时间。
接下来 mm 行,每行两个整数 SiSi 和 TiTi,表示一个玩家的起点和终点。
对于所有的数据,保证 1≤Si,Ti≤n1≤Si,Ti≤n,0≤Wj≤n0≤Wj≤n。
输出格式
输出到标准输出。
输出 11 行 nn 个整数,第 jj 个整数表示结点 jj 的观察员可以观察到多少人。
样例一
input
6 3 2 3 1 2 1 4 4 5 4 6 0 2 5 1 2 3 1 5 1 3 2 6
output
2 0 0 1 1 1
explanation
对于 11 号点,W1=0W1=0,故只有起点为 11 号点的玩家才会被观察到,所以玩家 11 和玩家 22 被观察到,共 22 人被观察到。
对于 22 号点,没有玩家在第 22 秒时在此结点,共 00 人被观察到。
对于 33 号点,没有玩家在第 55 秒时在此结点,共 00 人被观察到。
对于 44 号点,玩家 11 被观察到,共 11 人被观察到。
对于 55 号点,玩家 11 被观察到,共 11 人被观察到。
对于 66 号点,玩家 33 被观察到,共 11 人被观察到。
样例二
input
5 3 1 2 2 3 2 4 1 5 0 1 0 3 0 3 1 1 4 5 5
output
1 2 1 0 1
限制与约定
每个测试点的数据规模及特点如下表所示。提示:数据范围的个位上的数字可以帮助判断是哪一种数据类型。
| 测试点编号 | nn | mm | 约定 |
|---|---|---|---|
| 1 | =991=991 | =991=991 | 所有人的起点等于自己的终点,即 Si=TiSi=Ti |
| 2 | |||
| 3 | =992=992 | =992=992 | Wj=0Wj=0 |
| 4 | |||
| 5 | =993=993 | =993=993 | 无 |
| 6 | =99994=99994 | =99994=99994 | 树退化成一条链,其中 11 与 22 有边,22 与 33 有边,……,n−1n−1 与 nn 有边 |
| 7 | |||
| 8 | |||
| 9 | =99995=99995 | =99995=99995 | 所有的 Si=1Si=1 |
| 10 | |||
| 11 | |||
| 12 | |||
| 13 | =99996=99996 | =99996=99996 | 所有的 Ti=1Ti=1 |
| 14 | |||
| 15 | |||
| 16 | |||
| 17 | =99997=99997 | =99997=99997 | 无 |
| 18 | |||
| 19 | |||
| 20 | =299998=299998 | =299998=299998 |
时间限制:2s
空间限制:512MB
分析
看这份分析之前,请先查阅其他题解= =
对于一个点,显然能被其观察到的路径是满足 depth[S] = depth[i] + w[i] 或者 depth[S] = depth[i] - pathlen 的。
第二条式子建立在将起点投影至LCA上方的前提上
嗯... 先贴代码
//由于研究Zsnuo的代码,我短时间也没法写出完全独立的代码,干脆贴Zsnuo的好了= =Orz Zsnuo the Leader #include<cstdio> #include<algorithm> #include<cstring> #include<vector> using namespace std; const int N=300005; int n,m,u,v,cnt,s,t,anc,way; int time[N],ans[N],up[N*2],dn[N*2],c[N];//注意up数组和dn数组都要开两倍 int first[N],deep[N],f[N][25]; struct edge{int to,next;}e[N*2];//边表开两倍 vector<int>q1[N],q2[N],q3[N]; int read() { int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } void ins(int u,int v){cnt++;e[cnt].to=v;e[cnt].next=first[u];first[u]=cnt;} void dfs(int x) { for(int i=first[x];i;i=e[i].next) { int to=e[i].to; if(deep[to])continue;//节点to已出现过 deep[to]=deep[x]+1; f[to][0]=x;//to的父亲为x dfs(to); } } int lca(int ri,int rj)//倍增求最近公共祖先 { if(deep[ri]<deep[rj])swap(ri,rj); int d=deep[ri]-deep[rj]; for(int i=0;(1<<i)<=d;i++) if((1<<i)&d)ri=f[ri][i]; if(ri==rj)return ri; for(int i=16;i>=0;i--) if((1<<i)<=deep[rj]&&f[ri][i]!=f[rj][i]) ri=f[ri][i],rj=f[rj][i]; return f[ri][0]; } void DFS(int x,int last) { //向上的桶一律加N是为了防止减的时候出现负数 int u = dn[deep[x]+time[x]],v = up[deep[x]-time[x]+N],sz; // Be dealt as a normal node dn[deep[x]] += c[x];//节点x作为s出现 // No influ to his son Tree? sz=q1[x].size(); // The ima of S at T for(int i=0;i<sz;i++) up[q1[x][i]+N]++;//点x作为t出现 The ima of S at T for(int i=first[x];i;i=e[i].next) if(e[i].to!=last) DFS(e[i].to,x); ans[x] = dn[deep[x]+time[x]] + up[deep[x]-time[x]+N] -u-v; // Be dealt as a anc ++ //详见之前提到的公式,以及记得减去旧值 sz=q2[x].size(); // Now it's about to get out of the range of the path which makes now'node become a anc for(int i=0;i<sz;i++){ // If node'now is an anc dn[q2[x][i]]--; if(q2[x][i]==deep[x]+time[x]) // The pos of S at Anc ++ ans[x]--; } //如果是在lca处被检测到,记得减去重复情况 sz=q3[x].size(); for(int i=0;i<sz;i++)up[q3[x][i]+N]--; // The ima of S at Anc ++ //dfs退出lca时,更新两个桶 } int main() { n=read();m=read(); for(int i=1;i<n;i++) { u=read();v=read(); ins(u,v);ins(v,u); } deep[1]=1;//会影响后面dfs的判断 dfs(1); for(int j=1;j<=20;j++) for(int i=1;i<=n;i++) f[i][j]=f[f[i][j-1]][j-1];//递推出f数组 for(int i=1;i<=n;i++)time[i]=read(); for(int i=1;i<=m;i++) { s=read();t=read(); anc=lca(s,t);//最近公共祖先 way=deep[s]+deep[t]-2*deep[anc];//路径长度 c[s]++;//节点s作为起点出现的次数+1 q1[t].push_back(deep[t]-way); // The ima of S at T q2[anc].push_back(deep[s]); // The pos of S at anc q3[anc].push_back(deep[t]-way); // The ima of S at anc //前面提到的两条公式: //在s→lca这条路径上:deep[i]+w[i]=deep[s]; //在lca→t这条路径上:deep[i]-w[i]=deep[t]-way; //一个节点对ans的贡献从LCA开始,所以存在LCA的队列里 } DFS(1,0); for(int i=1;i<=n;i++)printf("%d ",ans[i]); return 0; }
根据源代码加了一些Chinglish的注释= =个人是觉得在Consolas的字体下写中文挺难看的
原帖地址:Zsnuo的NOIP补题记录
其实这份代码只是模拟,但是它优化的非常之迷= =
根据ljh2000的思路,我们需要把这些问题当作链处理。
显然这份代码就是这么干的,主要流程是向下推进时初始化操作范围,向上回溯时总结答案。
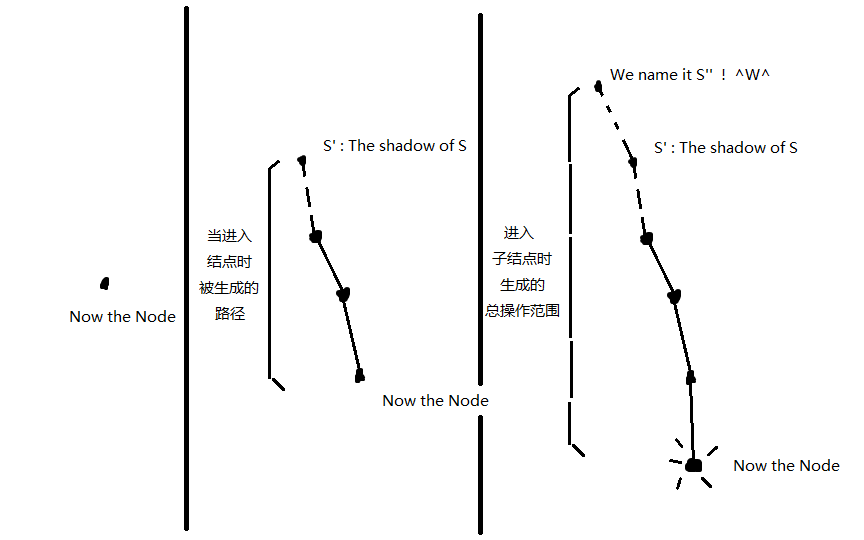
当我们DFS完进入一个新结点时,我们需要进行初始化,主要内容就是构建一条竖直方向的虚拟路径,通过将处于LCA另一端的S投影至LCA上方。
然后将当前点Now自身进行分析,也就是将 以now为起点的路径数量 添加进操作范围。
= =很迷
因为在该问题中我们把路径都基本投影为竖直方向的路径了,那么对于一个点,能产生贡献的起点要么在上方,要么在下方。
用两个桶进行维护的说法也就由此而生。
这时候又可以提到一个前提:如果一个点可以观察到某个玩家的路径,这个观察点必须在玩家的路径中。
那么对于一条路径,显然深度小于其LCA的观察点或者大于起点、终点的观察点就没必要观察了。
具体到代码中是这样体现的:
根据模拟过程我们可以发现,正在操作中的当前结点肯定是最低点,那么他不会影响到其子树的结算。
开始回溯时,代码会开始清除以当前结点为LCA的路径的结算信息,防止它们干扰到父节点的结算。
很神奇是不是= =
希望我以后还有心情回来重新写,到时候再对这篇题解进行修改。
代码

1 #include<cstdio> 2 #include<iostream> 3 #include<vector> 4 #define maxn 600005 5 using namespace std; 6 7 struct edge{ 8 int from,v; 9 }e[maxn]; 10 11 vector<int> q1[maxn],q2[maxn],q3[maxn]; 12 13 bool book[maxn]; 14 int n,ans[maxn],m,a,b,s,t; 15 int tot,first[maxn],depth[maxn],fa[maxn][20],down[maxn],up[maxn],c[maxn],w[maxn]; 16 void insert(int u,int v){ 17 tot++; 18 e[tot].from = first[u]; 19 e[tot].v = v; 20 first[u] = tot; 21 } 22 23 void dfs(int now){ 24 // cout << "A"; 25 for(int i = first[now];i;i = e[i].from){ 26 int v = e[i].v; 27 if(!depth[v]){ 28 depth[v] = depth[now]+1; 29 fa[v][0] = now; 30 for(int i = 1;i <= 18;i++) 31 fa[v][i] = fa[fa[v][i-1]][i-1]; 32 dfs(v); 33 } 34 } 35 } 36 37 int LCA(int u,int v){ 38 if(depth[u] < depth[v]) swap(u,v); 39 for(int i = 18;i >= 0;i--) 40 if(depth[fa[u][i]] >= depth[v]) 41 u = fa[u][i]; 42 if(u == v) return u; 43 for(int i = 18;i >= 0;i--) 44 if(fa[u][i] != fa[v][i]) 45 u = fa[u][i],v = fa[v][i]; 46 return fa[u][0]; 47 } 48 49 void DFS(int now){ 50 // cout << "B"; 51 int u = down[depth[now]+w[now]],v = up[depth[now]-w[now]+n]; 52 down[depth[now]] += c[now]; 53 54 int s1 = q1[now].size(); 55 for(int i = 0;i < s1;i++){ 56 up[q1[now][i]+n]++; 57 } 58 59 for(int i = first[now];i;i = e[i].from){ 60 if(!book[e[i].v]){ 61 book[e[i].v] = true; 62 DFS(e[i].v); 63 } 64 } 65 // cout << "C"; 66 ans[now] = up[depth[now]-w[now]+n] + down[depth[now]+w[now]] -u-v; // ? 67 68 int s2 = q2[now].size(); 69 for(int i = 0;i < s2;i++){ 70 down[q2[now][i]]--; 71 if(q2[now][i] == depth[now]+w[now]) 72 ans[now]--; 73 } 74 // cout << "D"; 75 int s3 = q3[now].size(); 76 for(int i = 0;i < s3;i++){ 77 up[q3[now][i]+n]--; 78 } 79 // cout << "E"; 80 } 81 82 int main(){ 83 scanf("%d%d",&n,&m); 84 85 for(int i = 1;i < n;i++){ 86 scanf("%d%d",&a,&b); 87 insert(a,b); 88 insert(b,a); 89 } 90 91 depth[1] = 1; 92 dfs(1); 93 94 95 for(int i = 1;i <= n;i++){ 96 scanf("%d",&w[i]); 97 } 98 99 for(int i = 1;i <= m;i++){ 100 scanf("%d%d",&s,&t); 101 c[s]++; 102 int anc = LCA(s,t); 103 int pathlen = depth[s]+depth[t]-2*depth[anc]; 104 q1[t].push_back(depth[t]-pathlen); 105 q2[anc].push_back(depth[s]); 106 q3[anc].push_back(depth[t]-pathlen); 107 } 108 109 book[1] = true; 110 DFS(1); 111 112 for(int i = 1;i <= n;i++){ 113 printf("%d ",ans[i]); 114 } 115 116 return 0; 117 }



