[SRM] 08 C

C-3 SRM 08

描述

给一个图，n 个点 m 条双向边，每条边有其长度。n 个点中有 k 个是特殊点，问任意两个特殊点的最短路是多少。

输入格式

第一行三个整数 n m k

第二行 k 个整数 ，为各个特殊点

接下来 m 行，每行三个整数 x y d，表示 x 到 y 有一条长度为 d 的边

输出格式

一个整数

样例输入

5 5 3
1 3 5
1 2 3
2 3 4
3 4 1
4 5 8
1 5 19

样例输出

7

数据范围与约定

• 图为联通图
• 
• 
• 
• 
• 

样例解释

样例中，1-3 的最短路为 7，3-5 的最短路为 9，1-5 的最短路为 16，因此答案为最小值 7

 

分析

想象所有的特殊点都在中央，而我们要求的就是：

 

 

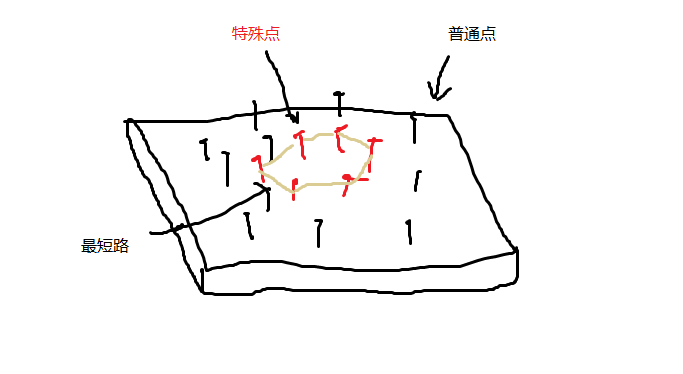
那么当那根被称为“最短路”的橡皮筋只捆在特殊点上时，其中的最短的一部分就是我们要求的。

那么当我们在找最优解的过程就像把这根橡皮筋从无关点上一个点一个点的向特殊点收缩。

这听起来有些玄幻。

非常套路地，我们需要求出每个点的最短路（也就是多源最短路），但同时还要记录对应的源点

这样当我们拎着一条边的时候，如果这条边两端的端点不同，这条边对应的橡皮筋的部分长度为 A点的最短路+边长+B点最短路。

这样我们可以在求最短路的过程中顺便求解。

 

代码

#include<cstdio>
#include<queue>
#include<iostream>
#define maxn_E 5050500
#define maxn_P 1010100
#define INF 2147483647
using namespace std;
typedef pair<int,int> node;
priority_queue<node,vector<node>,greater<node> > q;

struct edge{
    int from,v,len;
}e[maxn_E];

int first[maxn_P],tot,ans = INF,n,m,k,a,b,c,dis[maxn_P],sou[maxn_P],spe[maxn_P];
bool book[maxn_P];

void insert(int u,int v,int len){
    tot++;
    e[tot].from = first[u];
    e[tot].v = v;
    e[tot].len = len;
    first[u] = tot;
}

void dijkstra(){
    for(int i = 1;i <= n;i++) dis[i] = INF;
    for(int i = 1;i <= k;i++){
        q.push(make_pair(0,spe[i]));
        dis[spe[i]] = 0;
        sou[spe[i]] = spe[i];
    } 
    
    while(!q.empty()){
        node tmp = q.top();
        q.pop();
        
        int p = tmp.second;
        
        if(!book[p]){
            book[p] = true;
            for(int i = first[p];i;i = e[i].from){
                if(dis[p] != INF && dis[e[i].v] != INF && sou[p] != sou[e[i].v])
                        ans = min(ans,dis[p]+e[i].len+dis[e[i].v]);
                if(dis[e[i].v] > dis[p]+e[i].len && !book[e[i].v]){
                    if(sou[e[i].v] != sou[p])
                        sou[e[i].v] = sou[p];
                    dis[e[i].v] = dis[p]+e[i].len;
                    q.push(make_pair(dis[e[i].v],e[i].v));
//                    if(sou[p] != sou[e[i].v])
//                        ans = min(ans,dis[p]+e[i].len+dis[e[i].v]);
                }
            }
        }
    }
}

int main(){
    scanf("%d%d%d",&n,&m,&k);
    
    for(int i = 1;i <= k;i++) scanf("%d",&spe[i]);
    
    for(int i = 1;i <= m;i++){
        scanf("%d%d%d",&a,&b,&c);
        insert(a,b,c);
        insert(b,a,c);
    }
    
    dijkstra();
    
//    for(int i = 1;i <= n;i++){
//        printf("%d/%d ",dis[i],sou[i]);
//    }
    
    printf("%d",ans);
    
    return 0;
}