螺旋数组算法[下篇]--努力接近需求的本质

终于搞完了。

不过在周末看到了 flyinghearts 的算法，顿时觉得自己白干了，呵呵。

从他那里发现自己下面的算法分析还有改进的地方。

 

反正也糗大了，好歹留个纪念，第三篇博文如下。

我的算法有两个，其实是三个版本。

1、根据(x,y)坐标和矩形边长n，直接计算目标值，线性填充数组，非优化代码

2、根据(x,y)坐标和矩形边长n，直接计算目标值，线性填充数组，优化代码

3、将算法分散到两重循环之间，也就是说丧失了直接计算的能力，换取更高的执行速度。

 

先欣赏一种算法分析

首先我的思路是找到螺旋矩阵的规律，尤其是避免判断特定点在四条边。

结果我发现了一个新的规律(结果也就是死在这个分析上了，离真相就差一点点，结果是个谬误。中心1的位置不稳定，计划改成外旋顺时针再进行分析)

 

从内部的1开始，我们可以找到边长为2，3，4，5，6的螺旋矩阵

按照n边长，可以确定1的坐标，以1为第一块，(2,3,4)为第二块，以此类推。

我们可以根据(x,y)，和1的坐标，计算出(x,y)再哪块上。

然后进一步根据这些信息计算出该坐标上的数值

实际代码如下：

public void GenerateMatrixWithBeginingInfo(int N, int[,] matrix, int startAngle, bool isClockwish,bool isReverse)

{

if (isReverse == true)

this.reverse = -(N * N+1);

this.isClockwith = isClockwish;

this.angle = startAngle;

GenerateMatrix(N, matrix);

}

public void GenerateMatrixWithEndingInfo(int N, int[,] matrix, int endAngle, bool isClockwish,bool isReverse)

{

if (N % 2 != 1)

endAngle = (endAngle + 180) % 360;

this.GenerateMatrixWithBeginingInfo(N, matrix, endAngle, isClockwish,isReverse);

}

 

public void GenerateMatrix(int N, int[,] matrix)

{

 Point p;

 //Get point of origin

 originPoint = new Point { X = N / 2, Y = (N - 1) / 2 };

 

 for (int x = 0; x < N; x++)

 {

  for (int y = 0; y < N; y++)

  {

   //坐标转换

   p = processPoint(N, new Point { X=x,Y=y});

   matrix[x, y] = GetMatrixValue(N, p);

  }

 }

}

public int GetMatrixValue(int N, Point p)

{

 int blockNumber;

 int startNumber;

 int odd;

 odd = N % 2;

 //Get block number

 //1. get block number

 blockNumber = Math.Max(Math.Abs(p.X - originPoint.X), Math.Abs(p.Y - originPoint.Y)) * 2 + Convert.ToInt32(p.X + odd > p.Y);

 //2. get startNumber

 startNumber = blockNumber - blockNumber % 2;

 startNumber *= startNumber;

 //3. return value

 return Math.Abs((int)(startNumber + Math.Pow(-1,(blockNumber+1))*(p.X + p.Y-2*((N-blockNumber)/2)))+odd+reverse);

}

private Point processPoint(int N,Point p)

{

 int tmp;

 if (isClockwith == true)

 {

  switch (this.angle)

  {

   case 0:

    p.X = N - 1 - p.X;

    break;

   case 90:

    if (p.X + p.Y + 1 != N)

    {

     tmp = p.X;

     p.X = N - 1 - p.Y;

     p.Y = N - 1 - tmp;

    }

    break;

   case 180:

    p.Y = N - 1 - p.Y;

    break;

   case 270:

     if (p.X != p.Y)

    {

     tmp = p.X;

     p.X = p.Y;

     p.Y = tmp;

    }

    break;

  }

}

else

{

  switch(angle)

 {

   case 0:

    break;

   case 90:

    tmp = p.X;

    p.X = p.Y;

    p.Y = tmp;

    p.Y = N-1 - p.Y;

    break;

   case 180:

    p.Y = N-1 - p.Y;

    p.X = N-1 - p.X;

    break;

   case 270:

    tmp = p.X;

    p.X = p.Y;

    p.Y = tmp;

    p.X = N-1 - p.X;

    break;

   }

}

return p;

}

 

之所以要坐标转换，因为我默认是把偶数的块放在右上角，这样一来，奇数和偶数的情况下，最后结束的位置是不同的。

例如36在左上角，而25在右下角。

而一般螺旋矩阵的题目都是要求结束点是固定在一个地方的。

因此，我在实际数值计算之前先进行一次坐标转换。

这里这个坐标转换函数没有优化过，是最丑的一个了。

 

执行效率太恐怖了

不提了，太慢了

对于边长是1000的数组，我的代码是0.17~0.22秒，对比的一个模拟算法的代码只要0.008~0.009秒.

所以做了点优化（扔掉框架数学方法，采用位运算，减少函数调用...）

把代码的功能限定到只考虑从左上角外圈1开始到里面顺时针绕行。毕竟对比代码也只能干这个。要公平么

速度优化后的代码（不建议平时写这种可读性恐怖的代码，俺是被逼无奈，否则俺的乌龟算法没人要的。）

public void GenerateMatrix(int N, int[,] matrix)

{

int reverse, angle;

reverse = -(N * N + 1);

isClockwith = false;

if (N % 2 == 1)

angle = 180;

else

angle = 0;

int blockNumber; ;

int tmp;

int odd;

int value;

int blockX, blockY;

int x = 0, y = 0;

int n1=N-1;

ox = N / 2;

oy = (N - 1) / 2;

odd = N & 1;

int x1, y1;

for (x1 = 0; x1 < N; x1++)

{

if (angle == 0)

{

x = x1;

}

else

 

{

x = n1 - x1;

}

 

blockX = x - ox;

if (x < ox)

blockX = -blockX;

for (y1 = 0; y1 < N; y1++)

{

if (angle == 0)

{

y = y1;

}

else

{

y = n1 - y1;

}

blockY = y - oy;

if (blockY < 0)

blockY = -blockY;

 

if (blockX > blockY)

blockNumber = blockX<<1;

else

blockNumber = blockY<<1;

if (x > y || odd == 1 && x == y)

blockNumber++;

if (blockNumber != 1)

{

value=(blockNumber & (int.MaxValue - 1)) * (blockNumber & (int.MaxValue - 1));

if ((blockNumber &1) == 1)

{

value += x + y - ((N - blockNumber) & (int.MaxValue - 1));

}

else

{

value -= x + y - ((N - blockNumber) & (int.MaxValue - 1));

}

value += odd;

}

else

value = 1;

if (reverse == 0)

matrix[x1, y1] = value;

else

matrix[x1, y1] = -(value + reverse);

}

}

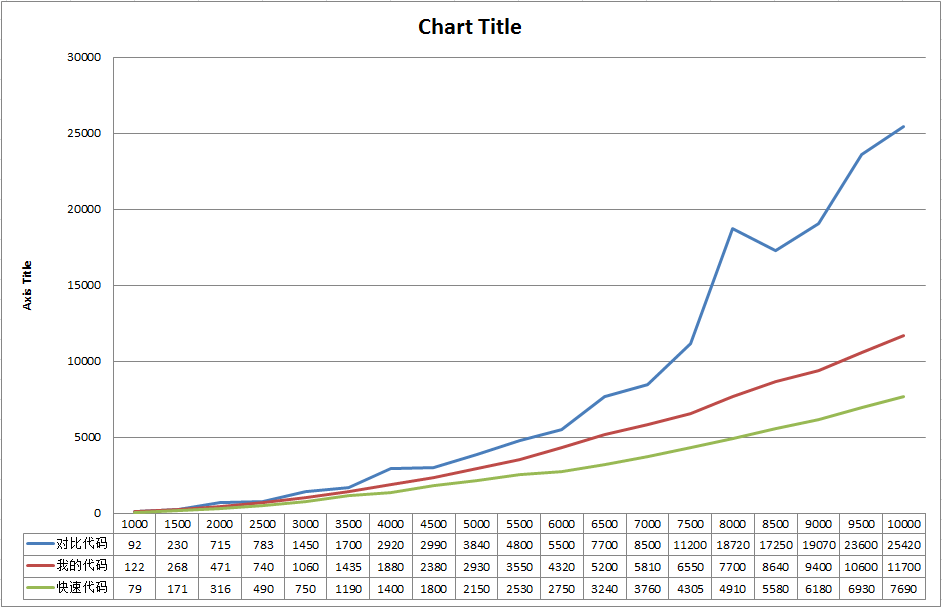
再测试结果如下：

 

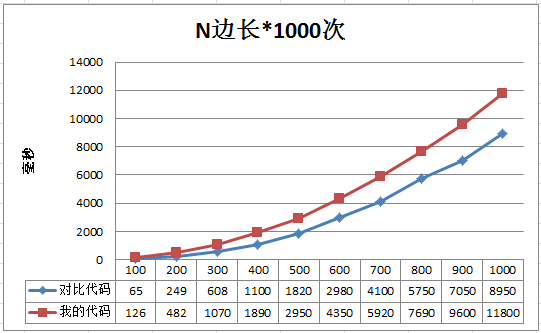
能看出一点点端倪，我的代码耗时随数组尺寸变化增长略慢一点

继续增加边长 

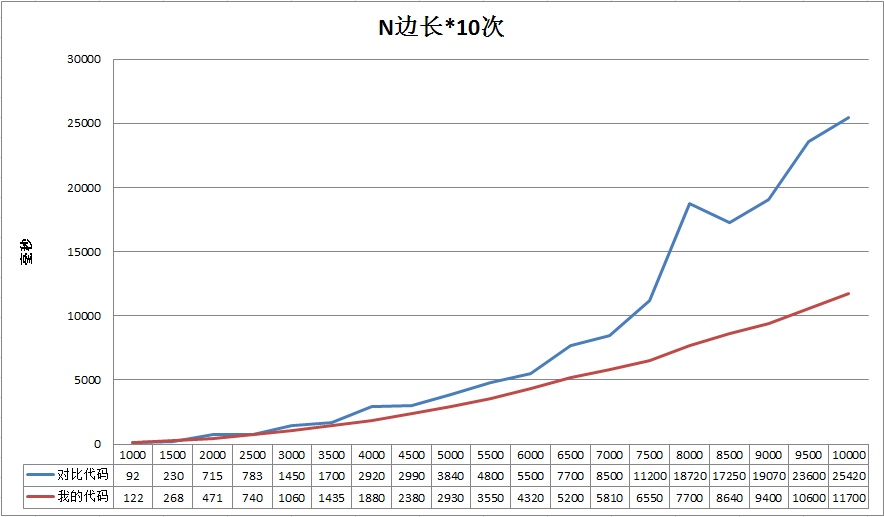
在边长达到2500以后，我的算法在速度上开始胜出。也就是说，虽然多了很多数学计算和逻辑判断，但是整体的执行速度反而快。

常识告诉我们，执行代码行越多越慢，因此这里比较靠谱的解释就是因为我的算法避免了对目标数组的非线性访问，从而在大数据量的时候开始拥有速度优势。

另外，直接模拟算法在边长3500以后出现了明显的不稳定，尤其是在8000这个位置（测了它好几遍，18720是一个极小值，平均值会更大）。而我的算法依然维持近似线性的增长。

具体原因没有深入调查，我认为是和老赵提到过的CPU缓存命中有关。

 

还能更快么？

最后，为了只求极限速度，同时也是在优化过程中发现有些计算步骤其实是可以分散到Y循环外部去的。

因此暂时先放弃用坐标和边长直接计算数值，转而写一个能顺序访问数组，且仅支持一个螺旋格式的最快速解。

其实这个算法早写了，世界独创的螺旋数组低于n(o^2)的生成算法 2010年3月14日发布

不过当时没同时发布算法代码

现在来欣赏算法分析

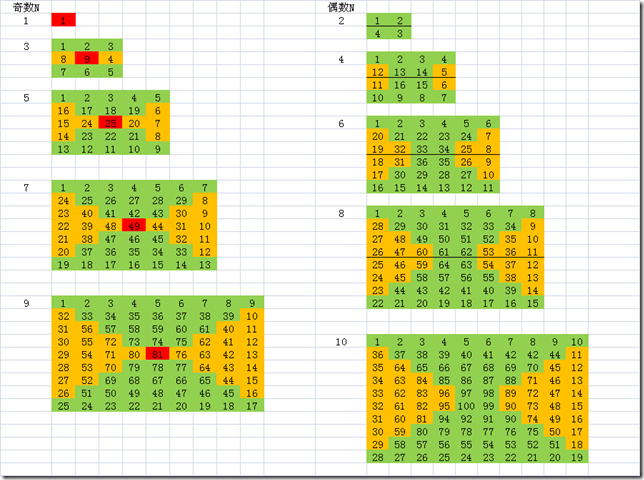
先看图

 

任何一行，都有3个部分组成

左边橙色的跳增部分，中间的递增递减部分，右边的跳减部分

第一行和最后一行特殊，没有左右部分，奇数边长的中心块归给上半边的递增部分。

每行的处理流程

0、行从0开始循环

1、计算必要参数

2、列从0开始循环

4、当前y坐标是否到达递增块起始位置，如是，转6

5、当前位置值等于本行跳增起始值加跳增增加值，转9

6、当前y坐标是否到达本行跳减起始位置，如是，转8

7、当前位置值等于本行跳增结束值加坐标计算偏移，转9

8、当前位置值等于本行跳减起始值加跳减增加值，转9

9、一行是否结束，是转0，否转2

10、所有结束

public void GenerateMatrix(int n, int[,] Matrix)

{

  int odd = n & 1;

  int point1, point2; //跳增结束点，递增结束点

  int base1 = 0, base2 = 0, base3 = 0;

  int magic;

  int n4;

  n4 = n * 4;

  magic = 4 * n - 7;

  //中间点x坐标

  int halfx = (n + 1) / 2; 

  //填充

  for (int x = 0; x < n;x++)

  {

   //计算结束点

   if (x < halfx)

   {

    point1 = x; //跳增结束点

    point2 = n - x; //跳减开始点

   }

   else//下半区

   {

    point1 = n - 1- x;

    point2 = x;

   }

   //跳增基数

   if (x == 0)

    base1 = 0;

   else if (x == n - 1)

   {

    base2 = 3 * n - 1;

   }

   else

   {

    base1 = n4 - 3 - x;

    if (x < halfx)

    {

     base2 = base1 + (n4 - 3 - (point1 << 2)) * (point1 - 1);

    }

   else

  {

    base2 = base1 + (n4 - 7 - (point1 << 2)) * point1 + 1;

   }

 }

  //跳减基数

  base3 = n + x;

  for (int y = 0; y < n; y++)

  {

  //跳增段

   if (y < point1)

   {

   //x基础数-x行控制+y基础数+y列控制

    Matrix[x, y] = base1+(magic-(y<<2))*y;

   }

   //递增段

   else if (y<point2)

   {

    if (x < halfx)

     Matrix[x, y] = base2+ y-x+1;

    else

    {

      Matrix[x, y] = base2 +point1-y-1;

    }

   }

   //跳减段

  else

  {

    Matrix[x, y] = base3+ (1+(y<<2)) * (n-1-y);

  }

 }

}

}

程序还是有细微的地方可以进一步优化速度。

不过目前的性能已经很明显了。

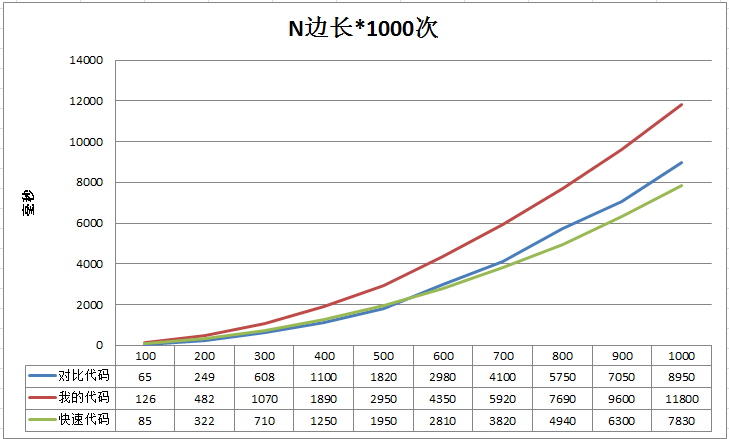
比较效果

 

 

呵呵，从边长600开始就超越了

 

一个关于算法效率的思考

我们一直在学算法复杂度：时间复杂度、空间复杂度。

如果仅从一般的估计而言，上面所有的算法都是O(n^2)的。

当边长增加一倍，算法需要的时间就会增加4倍。

但是很明显这种估计只是针对一个算法自身和自身进行比较，两个算法之间，即使大家都是O(n^2)，但是实际上还是有速度快慢之分的。

 

如果未来还能在性能上提高10%以上，我会再次发文的

呵呵。