elite_lcf 写了一篇 控制台输出螺旋型数字 的文章。刚好我记得在国家程序员资格考试的有关书籍里见过，并且当时曾试图写过一种不常规的实现。
在回帖中 AutumnWinter 给了个说法，时间复杂度应该不会小于O(n^2)。
这下让我比较有兴趣，因为传统的解法的确需要两重循环，而且无法再少了。
但是我的思路是另走捷径。通过一天的努力（周末泡汤了），终于写出来了。
不过实际测试的时候，在小数据量情况下没有优势，一定要在n>1400的时候才开始有几次领先，越后面领先越大
简单结果如下：
单位毫秒，数据仅表示一个趋势，不是绝对
VM7 内的虚拟机 win2003R2 1.5G P8600 2.4G
| N，执行5次 | elite_lcf C#改编 | 新算法 |
| 100 | 0ms | 15.622 |
| 800 | 62.49 | 62.49 |
| 2000 | 390 | 370 |
| 5000 | 2624 | 1937 |
| 10000 | 12000 | 7300 |
elite_lcf写的是C++的，我把它改成C#，因为我自己熟C#这块，惭愧。
下周用C++实现一把自己的算法再来骗点击。:-)
AutumnWinter 给出的另一个C++解法，由于其中利用了数组越界的一个判断，因此不去搞成C#的了，太烦了。
本文主要想提供一下基本思路，但是并不提供源码，以便有机会折磨一下园子里各位算法爱好者的大脑。(老子想这个算法可是费了点脑细胞的)
=========================================
这个图片是一切的开始
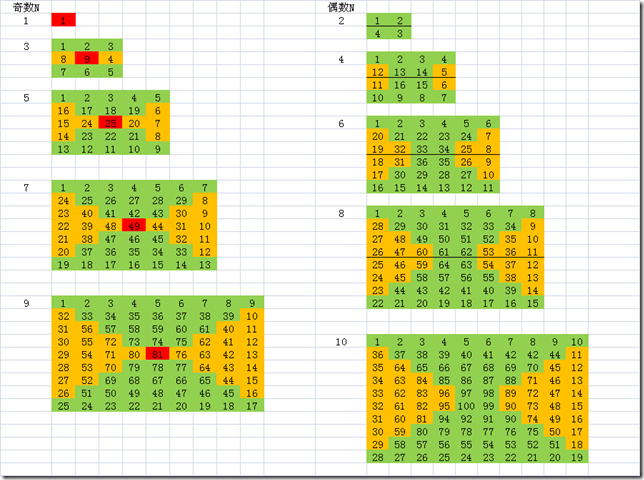
规律啊
这里面一定有一大把的规律，每个数字的位置和值都是函数确定相关的，只要能找出特定的关系，就能顺利填充数组。
比如，顶行和底行的和，与N是个函数关系，每层也一样
黄色的左右两边的和，也是一个函数关系。
绿色的行上下之间的差也有确定的函数关系。
我称之为行和、列和以及行差
我目前做到的，核心代码只要循环（O^2）/4的次数外加3-4个 n/2 次的循环就可以完成数组的填充了。核心就是只计算1/4面积，第二象限的内容，根据上述函数计算，填充另三个象限的对应值。
所以在大数据量的时候会有点优势。
算法，就是那么有趣。
PS：全国独家算法，自己研究出来的不追究，抄俺的公式必究（貌似还没公布公式呢）呵呵