Tutorial on Losses in Convolutional Neural Networks(edit 2)
Tutorial on Losses in Convolutional Neural Networks
Abstract
1. Introduction
2.Related Work
3. Cross-Entropy Loss
The Cross-Entropy Loss is actually the only loss we are discussing here. The other losses names written in the title are other variations of it. The Cross-Entropy Loss (CE Loss) is defined as:
$$CE = - \sum\limits_{i = 1}^C {{y_i}\log {z_i}} $$
where $y_i$ and $z_i$ is the groundtruth and the CNN score for each class i in C. As usually an activation function (sigmoid / softmax) is applied to the scores before the CE Loss computation, we denote ${a_i} = f({z_i})$ as the activations.
In a binary classification problem, where $C' = 2$ , the Cross Entropy Loss will be written as:
$$CE = - \sum\limits_{i = 1}^{{C^'} = 2} {{y_i}\log {z_i}} = - {y_1}\log {z_1} - (1 - {y_1})\log (1 - {z_1})$$
Where it assumes that there are two classes: ${c_1}$ and ${c_2}$. ${y_1}$ and ${z_1}$ are the groundtruth and score for ${c_1}$, and ${y_2}=1-{y_1}$ and ${z_2}=1-{z_1}$ are the groundtruth and score for ${c_2}$. That is the case when we split a Multi-Label classification problem in C binary classification problems.
3.1 Categorical Cross-Entropy Loss / Softmax Loss
Categorial Cross-Entropy Loss is a Softmax activation plus a Cross-Entropy Loss. if we use this loss, we will train a CNN to output a probability over C classes for each image. It is used in muti-class classification, where each image only has one positive class and its groundtruth is a one-hot vector.
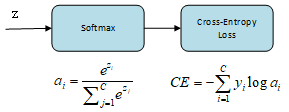
In the specific (and usual) case of Multi-Class classification the labels are one-hot, so only the positive class ${c_p}$ keeps its term in the loss. There is only one element of the groundtruth vector y which is not zero ${y_p} = 1$. So discarding the elements of the summation which are zero due to groundtruth labels, we can write:
$$CE = - \log {{{e^{{z_p}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}$$
Where ${z_p}$ is the CNN score for the positve class.
Defined the loss, now we’ll have to compute its gradient respect to the output neurons of the CNN in order to backpropagate it through the net and optimize the defined loss function tuning the net parameters. So we need to compute the gradient of CE Loss respect each CNN class score in z. The loss terms coming from the negative classes are zero. However, the loss gradient respect those negative classes is not cancelled, since the Softmax of the positive class also depends on the negative classes scores.
After some calculus, the derivative respect to the positive class is:
$${\partial \over {\partial {z_p}}}( - \log {{{e^{{z_p}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}) = {{{e^{{z_p}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }} - 1$$
And the derivative respect to the other (negative) classes is:
$${\partial \over {\partial {z_n}}}( - \log {{{e^{{z_p}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}) = {{{e^{{z_p}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}$$
Where ${y_n}$ is the score of any negative class in C different from ${c_p}$.
When Softmax loss is used is a multi-label scenario, the gradients get a bit more complex, since the loss contains an element for each positive class. Consider M are the positive classes of a sample. The CE Loss with Softmax activations would be:
$${1 \over M}\sum\limits_{i = 1}^M {( - \log {{{e^{{z_{{p_i}}}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}} )$$
Where each ${z_{{p_i}}}$ in M is the CNN score for each positive class. As in Facebook paper, I introduce a scaling factor 1/M to make the loss invariant to the number of positive classes, which may be different per sample.
The gradient has different expressions for positive and negative classes. For positive classes:
$${\partial \over {\partial {z_{{p_k}}}}}({1 \over M}\sum\limits_{i = 1}^M {( - \log {{{e^{{z_{{p_i}}}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}} )) = {1 \over M}(({{{e^{{z_{{p_k}}}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }} - 1) + (M - 1){{{e^{{z_{{p_k}}}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }})$$
Where ${{z_{{p_k}}}}$ is the score of any positive class.
For negative classes:
$${\partial \over {\partial {z_n}}}({1 \over M}\sum\limits_{i = 1}^M {( - \log {{{e^{{z_{{p_i}}}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}} )) = {{{e^{{z_n}}}} \over {\sum\nolimits_{j = 1}^C {{e^{{z_j}}}} }}$$
To be noticed all the formulas above are only for one example. To compute the loss for a batch size examples, we should add the individual losses up and divide it by the batch size number.
3.2 Binary Cross-Entropy Loss
Also called Sigmoid Cross-Entropy loss. It is a Sigmoid activation plus a Cross-Entropy loss. Unlike Softmax loss it is independent for each vector component (class), meaning that the loss computed for every CNN output vector component is not affected by other component values. That’s why it is used for multi-label classification, where the insight of an element belonging to a certain class should not influence the decision for another class. It’s called Binary Cross-Entropy Loss because it sets up a binary classification problem between C′=2 classes for every class in C, as explained above. So when using this Loss, the formulation of Cross Entroypy Loss for binary problems is often used:
$$CE = - \sum\limits_{i = 1}^{{C^'} = 2} {{y_i}\log {a_i}} = - {y_1}\log {a_1} - (1 - {a_1})\log (1 - {a_1})$$

This would be the pipeline for each one of the C clases. We set C independent binary classification problems (C′=2). Then we sum up the loss over the different binary problems: We sum up the gradients of every binary problem to backpropagate, and the losses to monitor the global loss. ${z_1}$ and ${y_1}$ are the score and the gorundtruth label for the class ${c_p}$, which is also the class ${c_i} in C. ${y_2}=1-{y_1}$ and ${z_2}=1-{z_1}$ are the groundtruth label and the score of the class ${c_n}$, which is not a “class” in our original problem with C classes, but a class we create to set up the binary problem with ${c_p}={c_i}$. We can understand it as a background class.
The loss can be expressed as:
$$CE = \left\{ {\matrix{
{ - \log ({a_1}){\rm{ }}if{\rm{ }}{y_1} = 1} \cr
{ - \log (1 - {a_1}){\rm{ }}if{\rm{ }}{y_1} = 0} \cr
} } \right.$$



