NOIP2018考前抱佛脚——图论基础复习

目录

• 存图方式
  • 邻接矩阵存图
  • 邻接表存图
  • 链式前向星
• 最小生成树
  • 例1 P1536 村村通
    • 题目描述
    • 输入输出格式
    • 输入输出样例
    • 标程
  • 例2 P1546 最短网络 Agri-Net
    • 题目背景
    • 题目描述
    • 输入输出格式
    • 输入输出样例
    • 标程
  • 例3 P1991 无线通讯网
    • 题目描述
    • 输入输出格式
    • 输入输出样例
    • 标程
• 最短路
  • 模板

存图方式

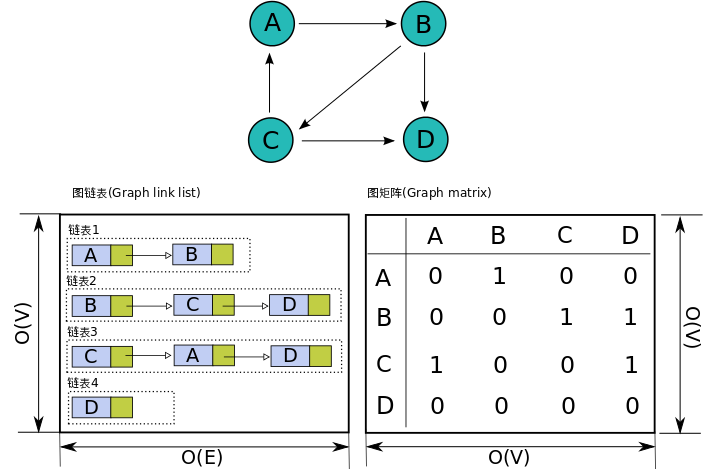
邻接矩阵存图

int map[MAXN][MAXM];

for(int i = 1;i <= n;++i)
{
	for(int j = 1;j <= m;++j)
	{
		int x = read(),y = read(),w = read();
		map[x][y] = w;
	}
}

邻接表存图

//最大顶点数 
const int MAXN = 100010;

// vector实现邻接表定义
vector<int> e[MAXN];

// 邻接表初始化操作
// 将起点为`i`的边链全部清空
e[i].clear();

// 增加边 i 到 j 的边
e[i].push_back(j);

// 查询边
for(int i = 0;i < n;++i)
{
	for(int j = 0;j < (int)e[i].size();++j)
	{
		//do something
	}
}

链式前向星

const int MAXN = 1000010;
const int MAXM = 1000010;

struct edge{
	int to; // 这条边的另外一个顶点 
	int next; // 下一条边的数组下标 
}e[MAXM];


//顶点 i 的第一条边的数组下标
int head[MAXN]; 

memset(head,-1,sizeof(head));

//存储 
inline void add(int x,int y,int id)
{
	edge[id].to = y;
	edge[id].next = head[x];
	head[x] = id;
}

//遍历
for(int i = head[x];i != -1;i = e[i].next)
{
	//do something
}

最小生成树

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAX_N = 50010;
const int MAX_M = 200000;
struct edge {
    int u,v,w;
    bool operator < (const edge &a)const{
    return w < a.w;
    }
}e[MAX_M];

int fa[MAX_N],n,m;

int get(int x){
    if(fa[x] == x){
        return fa[x];
    }
    return fa[x]=get(fa[x]);
}


int main() {
    
    cin>>n>>m;
    for(int i=0;i<m;i++){
        scanf("%d%d%d",&e[i].u,&e[i].v,&e[i].w);
    }
    sort(e,e+m);
    for(int i=1;i<=n;++i){
        fa[i]=i;
    }
    int sum=0;
    for(int i=0;i<m;++i){
        int x = get(e[i].u),y = get(e[i].v);
        if (x!=y){
            fa[x]=y;
            sum += e[i].w;
        }
    }
    printf("%d",sum);
    return 0;
}

例1 P1536 村村通

题目描述

某市调查城镇交通状况，得到现有城镇道路统计表。表中列出了每条道路直接连通的城镇。市政府“村村通工程”的目标是使全市任何两个城镇间都可以实现交通（但不一定有直接的道路相连，只要相互之间可达即可）。请你计算出最少还需要建设多少条道路？

输入输出格式

输入格式：

每个输入文件包含若干组测试测试数据，每组测试数据的第一行给出两个用空格隔开的正整数，分别是城镇数目N（N<1000）和道路数目M；随后的M行对应M条道路，每行给出一对用空格隔开的正整数，分别是该条道路直接相连的两个城镇的编号。简单起见，城镇从1到N编号。

注意：两个城市间可以有多条道路相通。例如：

3 3 1 2 1 2 2 1 这组数据也是合法的。当N为0时，输入结束。

输出格式：

对于每组数据，对应一行一个整数。表示最少还需要建设的道路数目。

输入输出样例

输入样例#1： 复制

4 2
1 3
4 3
3 3
1 2
1 3
2 3
5 2
1 2
3 5
999 0
0

输出样例#1： 复制

1
0
2
998

标程

#include<bits/stdc++.h>
int fa[20010];

int fin(int a){
    if(fa[a] == a) return a;
    else return fin(fa[a]);
}
int main(int argc, char const *argv[])
{
    int n; scanf("%d",&n);
    int m; 

    while(n){
        scanf("%d",&m);
        int t[10010];
        memset(t,0,sizeof(t));
        for(int i = 1;i <= n;i++ ) fa[i]=i;
        for(int i = 1;i <= m;i++ ){
            int a,b;
            scanf("%d%d",&a,&b);
            int k1=fin(b);
            fa[k1]=fin(a);
        }
        for(int i = 1; i <= n; i++) fa[i] = fin(fa[i]);
        for(int i = 1; i <= n; i++) t[fa[i]] ++;
        int ans=0;
        for(int i = 1; i <= 1000; i++) if(t[i]) ans++;
        printf("%d\n",ans-1);
        scanf("%d",&n);
    }
    return 0;
}

例2 P1546 最短网络 Agri-Net

题目背景

农民约翰被选为他们镇的镇长！他其中一个竞选承诺就是在镇上建立起互联网，并连接到所有的农场。当然，他需要你的帮助。

题目描述

约翰已经给他的农场安排了一条高速的网络线路，他想把这条线路共享给其他农场。为了用最小的消费，他想铺设最短的光纤去连接所有的农场。

你将得到一份各农场之间连接费用的列表，你必须找出能连接所有农场并所用光纤最短的方案。每两个农场间的距离不会超过100000

输入输出格式

输入格式：

第一行： 农场的个数，N（3<=N<=100）。

第二行..结尾: 后来的行包含了一个N*N的矩阵,表示每个农场之间的距离。理论上，他们是N行，每行由N个用空格分隔的数组成，实际上，他们限制在80个字符，因此，某些行会紧接着另一些行。当然，对角线将会是0，因为不会有线路从第i个农场到它本身。

输出格式：

只有一个输出，其中包含连接到每个农场的光纤的最小长度。

输入输出样例

输入样例#1： 复制

4
0 4 9 21
4 0 8 17
9 8 0 16
21 17 16 0

输出样例#1： 复制

28

标程

#include<bits/stdc++.h>
using namespace std;

const int MAX_N=101,MAX_M=10010;
int G[110][110];
const int INF=0x3f3f3f3f;
int fa[MAX_N],n,m;

struct kin
{
    int u,v,w;
}rxz[MAX_M];
bool cmp(kin x,kin y){
    return x.w<y.w;
}
int fin(int x){
    if(fa[x]==x) return fa[x];
    return fa[x]=fin(fa[x]);
}
int main(){
    scanf("%d",&n);
    memset(G,INF,sizeof(G));
    for(int i=0;i<n;i++){
        for(int j = 0; j < n; j++)
        {
            int w;
            scanf("%d",&w);
            if(w!=0) G[i][j]=w;
        }
    }
    int eid=0;
    
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
        {
            if(G[i][j]<INF){
                rxz[eid].u=i;
                rxz[eid].v=j;
                rxz[eid].w=G[i][j];
                eid++;
            }
        }    
    }
    
    sort(rxz,rxz+eid,cmp);/*
    for(int i = 0; i < eid; i++)
    {
        cout<<rxz[i].u<<ends<<rxz[i].v<<ends<<rxz[i].w<<endl;
    }*/
    
    for(int i = 1; i <= MAX_N; ++i)
    {
        fa[i]=i;
    }
    int rest = n,ans=0;
    for(int i = 0; i < eid && rest>1; ++i)
    {
        int x = fin(rxz[i].u),y=fin(rxz[i].v);
        if (x!=y) {
            fa[x]=y;
            //cout<<rxz[i].w<<ends;
            ans = ans + rxz[i].w;
            rest--;
            //cout<<ans<<endl;
        }
    }
    
    printf("%d",ans);

    return 0;
}

例3 P1991 无线通讯网

题目描述

国防部计划用无线网络连接若干个边防哨所。2 种不同的通讯技术用来搭建无线网络；

每个边防哨所都要配备无线电收发器；有一些哨所还可以增配卫星电话。

任意两个配备了一条卫星电话线路的哨所（两边都ᤕ有卫星电话）均可以通话，无论

他们相距多远。而只通过无线电收发器通话的哨所之间的距离不能超过 D，这是受收发器的功率限制。收发器的功率越高，通话距离 D 会更远，但同时价格也会更贵。

收发器需要统一购买和安装，所以全部哨所只能选择安装一种型号的收发器。换句话说，每一对哨所之间的通话距离都是同一个 D。你的任务是确定收发器必须的最小通话距离 D，使得每一对哨所之间至少有一条通话路径（直接的或者间接的）。

输入输出格式

输入格式：

从 wireless.in 中输入数据第 1 行，2 个整数 S 和 P，S 表示可安装的卫星电话的哨所数，P 表示边防哨所的数量。接下里 P 行，每行两个整数 x，y 描述一个哨所的平面坐标(x, y)，以 km 为单位。

输出格式：

输出 wireless.out 中

第 1 行，1 个实数 D，表示无线电收发器的最小传输距离，精确到小数点后两位。

输入输出样例

输入样例#1： 复制

2 4
0 100
0 300
0 600
150 750

输出样例#1： 复制

212.13

标程

#include<bits/stdc++.h>
using namespace std;

int fa[520];

struct edge
{
    int u,v;
    double w;
    bool operator < (const edge &a)
    {
        return w < a.w;
    }
}G[300010];

inline int fin(int x)
{
    return fa[x] == x ? x : fa[x] = fin(fa[x]);
}

int main(int argc, char const *argv[])
{
    int x[520],y[520];
    int s,p,num;
    cin >> s >> p;
    num = p;
    for(int i = 1;i <= p;++i)
    {
        fa[i] = i;
        cin >> x[i] >> y[i];
    }

    int k = 0;

    for(int i = 1;i <= p;++i)
    {
        for(int j = 1;j <= p;++j)
        {
            G[k].u = i;
            G[k].v = j;
            G[k].w = sqrt((x[i] - x[j])*(x[i] - x[j]) + (y[i] - y[j])*(y[i] - y[j]));
            k++;
        }
    }

    sort(G,G+k);

    int i;
    for(i = 0;i < k;++i)
    {
        int nx = fin(G[i].u) ,  ny = fin(G[i].v);
        if(nx != ny)
        {
            fa[nx] = fin(fa[ny]);
            num--;
        }
        if(num <= s) break;
    }

    printf("%.2lf",G[i].w);

    return 0;
}

最短路

模板

#include<bits/stdc++.h>
#define P std::pair<long long,int >

const int MAXN = 100086;
const int MAXM = 521314;
const int inf = 0x7fffffff;

inline int read()
{
	int x = 0,t = 1; char ch = getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')t=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*t;
}

struct edge{
	int u,v,w,next;
}e[MAXM];

int head[MAXN],dis[MAXN],cnt;
bool vis[MAXN];
int n,m,s;

std::priority_queue<P,std::vector<P>,std::greater<P> > q;

inline void add(int u,int v,int w)
{
	cnt++;
	e[cnt].w = w;
	e[cnt].u = u;
	e[cnt].v = v;
	e[cnt].next = head[u];
	head[u] = cnt;
}

inline void init()
{
	n = read(); m = read(); s = read();
	for(int i = 1;i <= m;++i)
	{
		int x = read(),y = read(),w = read();
		add(x,y,w);
	}
	
	for(int i = 0;i <= n;++i)
		dis[i] = inf;
	
	dis[s] = 0;
	q.push(std::make_pair(0,s));
	
	while(!q.empty())
	{
		int x = q.top().second;
		q.pop();
		
        if(!vis[x])
        {
            vis[x]=1;
            for(int i = head[x];i;i = e[i].next)
            {
                int v = e[i].v;
                dis[v] = std::min(dis[v],dis[x]+e[i].w);
                q.push(std::make_pair(dis[v],v));
            }
        }
	}

    for(int i=1;i<=n;i++)
    {
        printf("%d ",dis[i]);
    }
}

int main(void)
{
	init();
	return 0;
}