44. 通配符匹配

DP的思路：

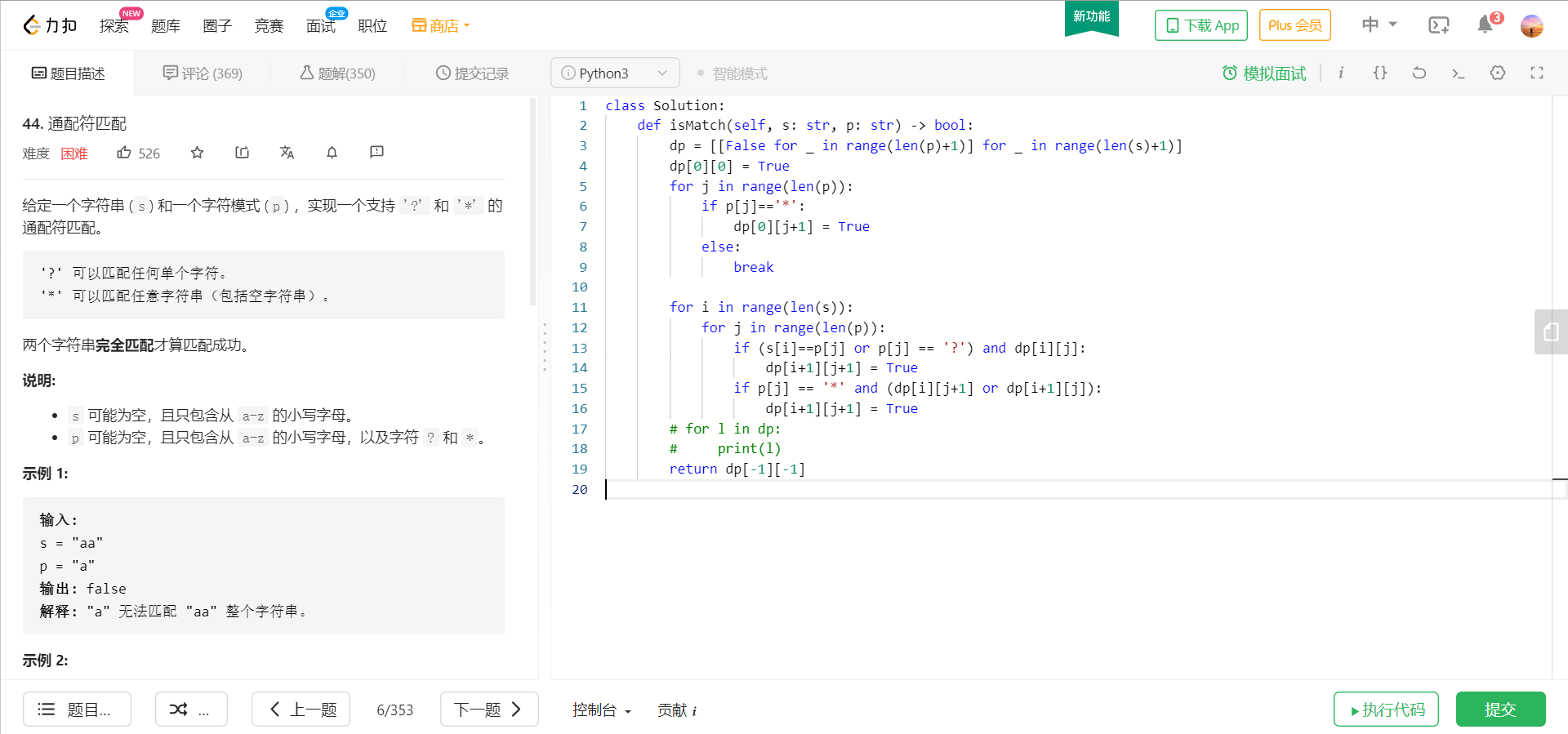
　　1. 通常dp第一个难点都是找状态转移方程，对于 s中前i个字符与p中前j个字符：

　　　　1）p[j] == s[i] && dp[i-1][j-1]   =>  dp[i][j] = True

　　　　2)   p[j]  == '?'  && dp[i-1][j-1]  =>  dp[i][j] = True

　　　　3)   p[j] == '*'   

　　　　　　(1) 选择不使用*，则dp[i][j] = dp[i][j-1]

　　　　　　(2) 选择使用*，则dp[i][j]  = dp[i-1][j]  

　　　　　 （3）综合起来  dp[i][j] = dp[i][j-1] or dp[i-1][j]  

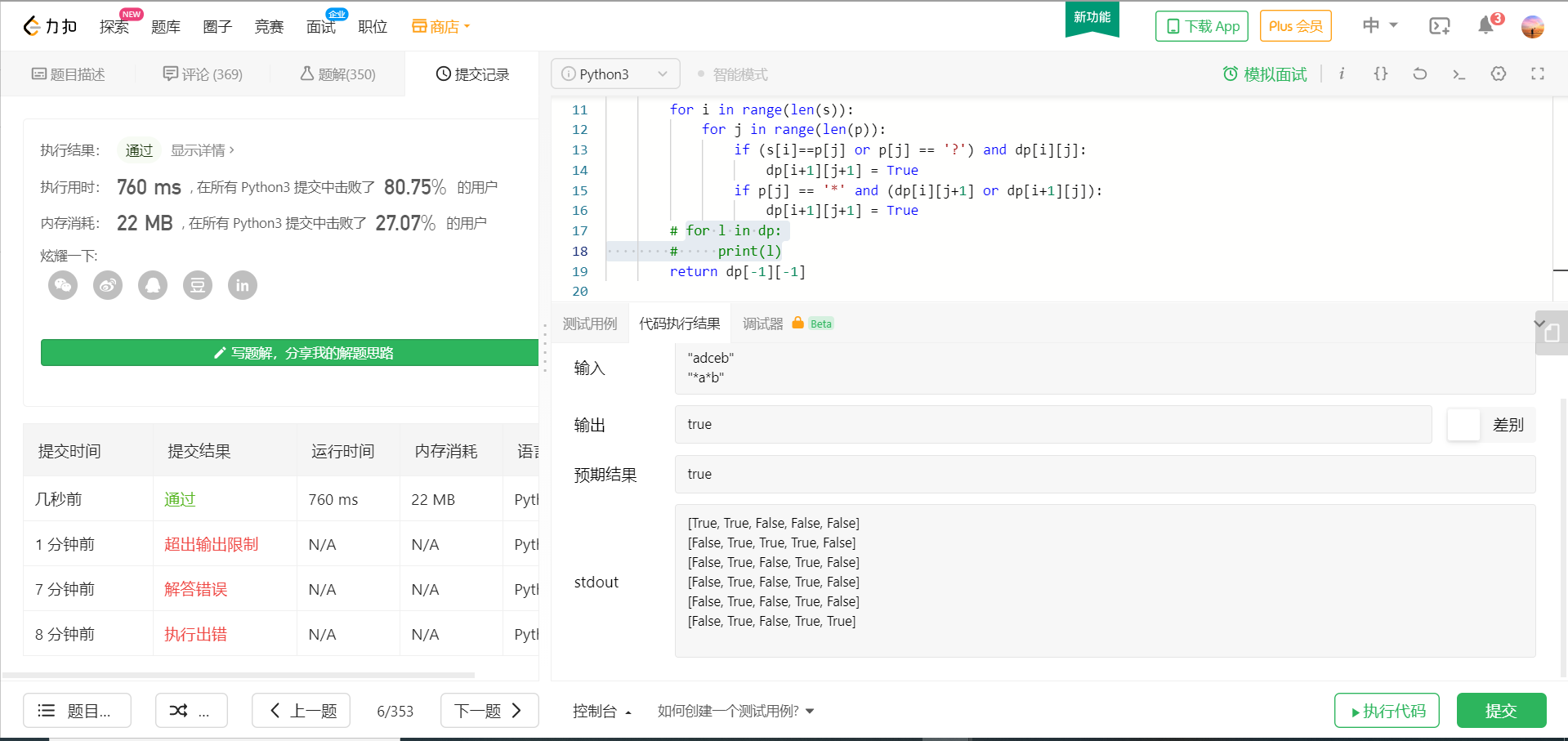
　　　　4) 对于 ‘3)’中的情况，其实很难理解，这里需要过一下s,j的双重循环，理解怎么在遍历

　　　　　　（1） 首先对于s[0]遍历p中每一个字符，看能否匹配，如果s[0]是‘*’，则能完全匹配p，则dp[0][0-j-1]都是True

　　　　　　（2） 再看s[1]，看能匹配到哪里，然后s[2].....

　　　　　　（3） 所以 3.1中不使用‘*’的意思是，看s[i]在j=0~j=len(p)-1的过程中，能不能匹配s[i][j-1]

　　　　　　（4） 3.2中使用的意思是，对于上一个s字符s[i-1]是否已经匹配过p[j]

　　　　　　（5） 综上，弄清楚dp的遍历顺序对于理解  p[j] == '*'  的情况很重要

　　2. dp中的第二个难点是dp初始化

　　　　1）本题是顺序遍历，需要用到 dp[i-1][j-1] dp[i-1][j] dp[i][j-1] ，所以初始化时需要在前面预留一行一列

　　　　2）dp[0][0] = True 

　　　　3)  对于dp[0][j]，如果p一直是‘*’，则可一直匹配空串