SVM函数中的两个超参数 C gamma
SVM的优缺点(复习)
https://blog.csdn.net/qq_38734403/article/details/80442535
https://blog.csdn.net/u012879957/article/details/82459315
https://www.cnblogs.com/hxsyl/p/5231389.html
核函数的基本作用就是接受两个低维空间里的向量,能够计算出经过某个变换后在高维空间里的向量内积值。
RBF 核与多项式核相比具有参数少的优点
用交叉验证找到最好的参数 C 和γ 。使用 RBF 核时,要考虑两个参数 C 和γ 。因为参数的选择并没有一定的先验知识,必须做某种类型的模型选择(参数搜索)。目的是确定好的(C,γ)使得分类器能正确的预测未知数据(即测试集数 据),有较高的分类精确率。值得注意的是得到高的训练正确率即是分类器预测类标签已知的训练数据的正确率)不能保证在测试集上具有高的预测精度。因此,通 常采用交叉验证方法提高预测精度。k 折交叉验证(k-fold cross validation)
C为惩罚系数,C越大,对误差越重视,容易overfitting,C越小,对误差惩罚小,容忍大,越偏向soft margin
gamma大,![]() 会比较小,会使高斯分布又瘦又长,会存在overffting ,原文如下
会比较小,会使高斯分布又瘦又长,会存在overffting ,原文如下
此外大家注意RBF公式里面的sigma和gamma的关系如下:
这里面大家需要注意的就是gamma的物理意义,大家提到很多的RBF的幅宽,它会影响每个支持向量对应的高斯的作用范围,从而影响泛化性能。我的理解:如果gamma设的太大,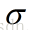
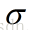
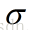

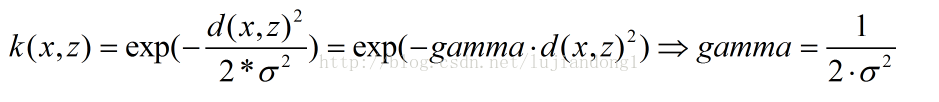

 浙公网安备 33010602011771号
浙公网安备 33010602011771号