第二部分 高数_9 优化
9、优化
（1）最小二乘法
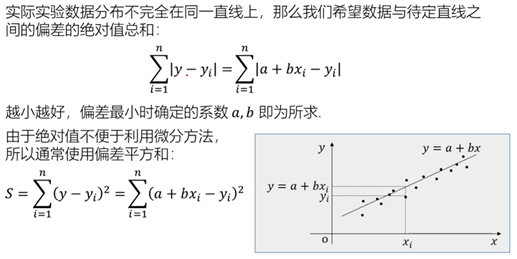
只要知道
就可以求出a和b的值
注意：若在实验过程中，实验数据在坐标系中的分布类似指数函数，那么可以考虑经验公式的形式为y=aebx，那么可以将它变形为lny = lna + bx ,如此便是新型函数的形式。
（2）梯度下降
（3）牛顿法
牛顿法是一种用来求解可微函数的近似解的方法。
牛顿法具有二次收敛性，因此比普通的梯度下降收敛的更快。
下图中绿色的线路为梯度下降法的路线，红色为牛顿法的下降路线。
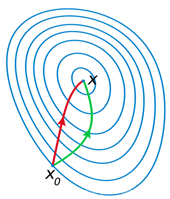
牛顿法在迭代的时候，需要计算Hessian矩阵，当维度较高的时候，计算Hessian矩阵比较困难。
关于牛顿法的具体知识点参照：
https://blog.csdn.net/HouDouZhou/article/details/85988847
https://www.cnblogs.com/ljy2013/p/5129294.html
