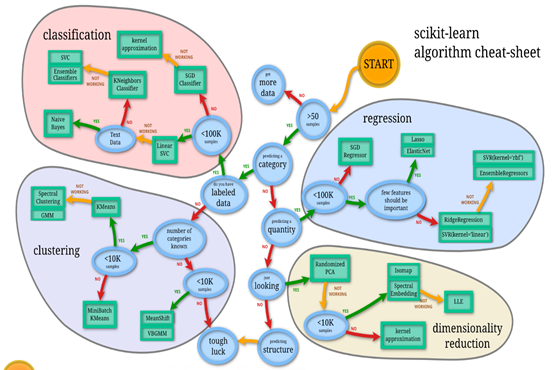
第6章 挖掘建模
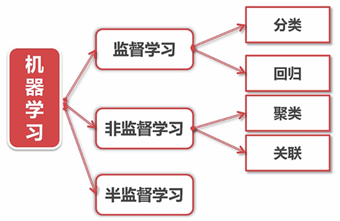
学习:通过接收到的数据,归纳提取相同与不同
机器学习:让计算机以数据为基础,进行归纳与总结
模型:数据解释现象的系统。
6:2:2
· 训练集:用来训练与拟合模型
· 测试集:模型泛化能力的考量。(泛化:对数据的预测能力)
· 验证集:当通过训练集训练出多个模型后,使用验证集数据纠偏或比较预测
当数据量样本较少时:
K-fold交叉验证:将数据集分成K份,每份轮流作一遍测试集,其他作训练集

其中罗基斯特映射和人工神经网络既可以做回归,也可以做分类,但是其作用主要以回归为主。
6.1 分类
6.1.1 KNN

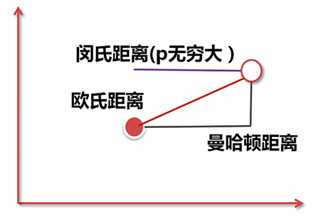

步骤如下:
1)算距离:给定测试对象,计算它与训练集中的每个对象的距离
2)找邻居:圈定距离最近的k个训练对象,作为测试对象的近邻
3)做分类:根据这k个近邻归属的主要类别,来对测试对象分类
import numpy as np
import pandas as pd
from sklearn.preprocessing import MinMaxScaler,StandardScaler,LabelEncoder,OneHotEncoder,Normalizer
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.decomposition import PCA
pd.set_option('display.max_columns',None) #控制列的输出
#sl:satisfaction_level ---- False:MinMaxScaler;True:StandardScaler
#le:last_evaluation ---- False:MinMaxScaler;True:StandardScaler
#npr:number_project ---- False:MinMaxScaler;True:StandardScaler
#amh:average_monthly_hours ---- False:MinMaxScaler;True:StandardScaler
#tsc:time_spend_company ---- False:MinMaxScaler;True:StandardScaler
#wa:Work_accident ---- False:MinMaxScaler;True:StandardScaler
#pl5:promotion_last_5years ---- False:MinMaxScaler;True:StandardScaler
#dp:department ---- False:LabelEncoder;True:OneHotEncoder
#slr:salary ---- False:LabelEncoder;True:OneHotEncoder
def hr_preprocessing(sl = False,le = False,npr = False,amh = False,tsc = False,
wa = False,pl5 = False,dp = False,slr = False,lower_d = False,ld_n = 1):
df = pd.read_csv('yuanHR.csv')
# 1、清洗数据--即去除异常值或抽样
df = df.dropna(subset=['satisfaction_level','last_evaluation'])
df = df[df['satisfaction_level']<=1][df['salary']!='nme']
# 2、得到标注
label = df['left']
df = df.drop('left', axis=1)
#3、特征选择
#4、特征处理
scaler_lst = [sl,le,npr,amh,tsc,wa,pl5]
column_lst = ['satisfaction_level','last_evaluation','number_project',
'average_monthly_hours','time_spend_company','Work_accident',
'promotion_last_5years']
for i in range(len(scaler_lst)):
if not scaler_lst[i]:
df[column_lst[i]] = \
MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
else:
df[column_lst[i]] = \
StandardScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
scaler_lst = [slr, dp]
column_lst = ['salary', 'department']
for i in range(len(scaler_lst)):
if not scaler_lst[i]:
if column_lst[i] == 'salary':
df[column_lst[i]] = [map_salary(s) for s in df['salary'].values]
else:
df[column_lst[i]] = LabelEncoder().fit_transform(df[column_lst[i]])
#將'salary', 'department'进行归一化处理
df[column_lst[i]] = MinMaxScaler().fit_transform(df[column_lst[i]].values.reshape(-1,1)).reshape(1,-1)[0]
else:
#pandas库中提供的直接进行OneHotEncoder的方法是get_dummies()
df = pd.get_dummies(df,columns=[column_lst[i]])
if lower_d == True:
return PCA(n_components=ld_n).fit_transform(df.values)
return df,label
d =dict([("low",0),('medium',1),('high',2)])
def map_salary(s):
return d.get(s,0)
#在sklearn中没有函数可以一步将训练集、验证集、测试集一步切分的函数,但有train_test_split函数可一步切分训练集和测试集
def hr_modeling(features,label):
from sklearn.model_selection import train_test_split
f_v = features.values
l_v = label.values
#得到验证集,占比20%
X_tt,X_validation,Y_tt,Y_validation= train_test_split(f_v,l_v,test_size=0.2)
#得到测试集,占比20%
X_train,X_test,Y_train,Y_test = train_test_split(X_tt,Y_tt,test_size=0.25)
print('train:',len(X_train),'\n','validation:',len(X_validation),'\n','test',len(X_test))
#KNN
#NearestNeighbors可以直接获取一个点附近的若干个点
from sklearn.neighbors import NearestNeighbors,KNeighborsClassifier
#通过比较,k=3时的效果比较好,所以固定模型选择k=3
knn_clf = KNeighborsClassifier(n_neighbors=3)
# knn_clf_n5 = KNeighborsClassifier(n_neighbors=5)
#进行拟合
knn_clf.fit(X_train,Y_train)
# knn_clf_n5.fit(X_train, Y_train)
#验证:用验证集进行对比
Y_pred_validation = knn_clf.predict(X_validation)
# Y_pred_validation_n5 = knn_clf_n5.predict(X_validation)
#衡量指标:准确率、召回率、F值
from sklearn.metrics import accuracy_score,recall_score,f1_score
print('针对验证集,选择3个邻居时:')
print("accuracy_score:",accuracy_score(Y_validation,Y_pred_validation))
print("recall_score:",recall_score(Y_validation,Y_pred_validation))
print("f1_score:",f1_score(Y_validation,Y_pred_validation))
# print('\n','选择5个邻居时:')
# print("accuracy_score:", accuracy_score(Y_validation, Y_pred_validation_n5))
# print("recall_score:", recall_score(Y_validation, Y_pred_validation_n5))
# print("f1_score:", f1_score(Y_validation, Y_pred_validation_n5))
#针对测试集
Y_pred_test = knn_clf.predict(X_test)
print('针对测试集,选择3个邻居时:')
print("accuracy_score:",accuracy_score(Y_test,Y_pred_test))
print("recall_score:",recall_score(Y_test,Y_pred_test))
print("f1_score:",f1_score(Y_test,Y_pred_test))
# 针对训练集
Y_pred_train= knn_clf.predict(X_train)
print('针对训练集,选择3个邻居时:')
print("accuracy_score:", accuracy_score(Y_train, Y_pred_train))
print("recall_score:", recall_score(Y_train, Y_pred_train))
print("f1_score:", f1_score(Y_train, Y_pred_train))
#对训练出的模型进行存储
from sklearn.externals import joblib
#对训练出的模型进行存储,取名为knn_clf_model
joblib.dump(knn_clf,'knn_clf_model')
#使用模型
knn_clf = joblib.load('knn_clf_model')
#利用存储的模型进行计算
Y_pred_train = knn_clf.predict(X_train)
print('利用存储的模型针对训练集进行计算:')
print("accuracy_score:", accuracy_score(Y_train, Y_pred_train))
print("recall_score:", recall_score(Y_train, Y_pred_train))
print("f1_score:", f1_score(Y_train, Y_pred_train))
def main():
features,label = hr_preprocessing()
hr_modeling(features,label)
if __name__ == "__main__":
main()
'''
train: 8999
validation: 3000
test 3000
针对验证集,选择3个邻居时:
accuracy_score: 0.955
recall_score: 0.9283667621776505
f1_score: 0.9056603773584906
针对测试集,选择3个邻居时:
accuracy_score: 0.9523333333333334
recall_score: 0.9252717391304348
f1_score: 0.9049833887043189
针对测试集,选择3个邻居时:
accuracy_score: 0.9745527280808979
recall_score: 0.9611605053813758
f1_score: 0.9471985243255706
利用存储的模型针对训练集进行计算:
accuracy_score: 0.975108345371708
recall_score: 0.9569332702318978
f1_score: 0.9475164011246485
'''
6.1.2 朴素贝叶斯

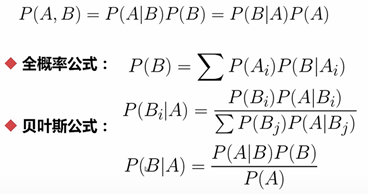
拉普拉斯平滑:在算条件概率时,给分母加上一个Ni(表示第i个属性可能取的值),给分子加一个1
https://scikit-learn.org/stable/modules/classes.html#module-sklearn.naive_bayes
说明:在运用朴素贝叶斯时,所用的特征必须是离散值;若这些离散值是二值的,那么就用BernoulliNB效果较好一些;若这些离散值是连续的,那么在BernoulliNB算法下也会先将这些离散值进行二值化。若特征服从高斯分布,那么就使用GaussianNB。
在hr_modeling()中进行处理,此处重复代码不再给出
from sklearn.naive_bayes import GaussianNB,BernoulliNB
#对模型进行统一管理
models = []
#通过比较,k=3时的效果比较好,所以固定模型选择k=3
# knn_clf = KNeighborsClassifier(n_neighbors=3)
models.append(('KNN',KNeighborsClassifier(n_neighbors=3)))
models.append(('GaussianNB',GaussianNB()))
models.append(('BernoulliNB',BernoulliNB()))
print('0:训练集 1:验证集 2:测试集')
for clf_name,clf in models:
clf.fit(X_train,Y_train)
xy_lst =[(X_train,Y_train),(X_validation,Y_validation),(X_test,Y_test)]
for i in range(len(xy_lst)):
X_part = xy_lst[i][0]
Y_part = xy_lst[i][1]
Y_pred = clf.predict(X_part)
print(i)
from sklearn.metrics import accuracy_score, recall_score, f1_score
print(clf_name,'准备率:',accuracy_score(Y_part,Y_pred),
'召回率:',recall_score(Y_part,Y_pred),
'F1分数:',f1_score(Y_part,Y_pred))
'''
0:训练集 1:验证集 2:测试集
0
KNN 准确率: 0.974997221913546 召回率: 0.955607476635514 F1分数: 0.947856315179606
1
KNN 准确率: 0.9556666666666667 召回率: 0.9348441926345609 F1分数: 0.9084652443220922
2
KNN 准确率: 0.9586666666666667 召回率: 0.926896551724138 F1分数: 0.9155313351498638
0
GaussianNB 准确率: 0.7957550838982109 召回率: 0.735981308411215 F1分数: 0.6315156375300721
1
GaussianNB 准确率: 0.7923333333333333 召回率: 0.7450424929178471 F1分数: 0.6280597014925373
2
GaussianNB 准确率: 0.813 召回率: 0.7489655172413793 F1分数: 0.6593806921675773
0
BernoulliNB 准确率: 0.8402044671630181 召回率: 0.47757009345794393 F1分数: 0.5870189546237794
1
BernoulliNB 准确率: 0.846 召回率: 0.49291784702549574 F1分数: 0.6010362694300518
2
BernoulliNB 准确率: 0.8393333333333334 召回率: 0.4731034482758621 F1分数: 0.5873287671232877
'''

|
|
生成模型 |
判别模型 |
|
对数据要求 |
高 |
低 |
|
对数据容忍度 |
小 |
大 |
|
速度 |
快 |
慢 |
|
使用范围 |
窄 |
广 |
6.1.3 决策树

决策树切分方法
· 信息增益-ID3(依次选择Gain值最大的特征进行切分)
· 信息增益率-C4.5
· Gini系数-CART(依次选择不纯度最低的进行切分,Gini可参见4.2.2分组与钻取)


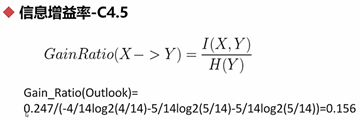

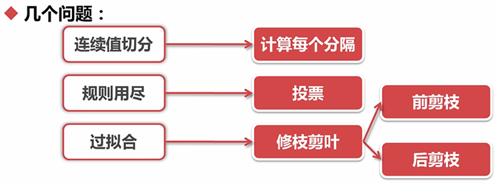
绘制决策树---生成pdf文件
仍然在hr_modeling()中进行处理,此处重复代码不再给出
import pydotplus #和Graphvia一样,用于决策树图形的绘制 from sklearn.tree import DecisionTreeClassifier,export_graphviz from sklearn.externals.six import StringIO models = [] #DecisionTreeClassifier()的criterion参数默认是gini #选择最小不纯度切分为0.1 models.append(('DecisionTreeGini',DecisionTreeClassifier(min_impurity_split=0.1))) models.append(('DecisionTreeEntroy',DecisionTreeClassifier(criterion='entropy'))) print('0:训练集 1:验证集 2:测试集') for clf_name,clf in models: clf.fit(X_train,Y_train) xy_lst =[(X_train,Y_train),(X_validation,Y_validation),(X_test,Y_test)] for i in range(len(xy_lst)): X_part = xy_lst[i][0] Y_part = xy_lst[i][1] Y_pred = clf.predict(X_part) print(i) from sklearn.metrics import accuracy_score, recall_score, f1_score print(clf_name,'准确率:',accuracy_score(Y_part,Y_pred), '召回率:',recall_score(Y_part,Y_pred), 'F1分数:',f1_score(Y_part,Y_pred)) if clf_name =='DecisionTreeGini' or clf_name=='DecisionTreeEntroy': #dot_data这两种写法等效 dot_data = StringIO() export_graphviz(clf, out_file=dot_data, feature_names=f_names, class_names=["NL", "L"], filled=True, rounded=True, special_characters=True) graph = pydotplus.graph_from_dot_data(dot_data.getvalue()) # dot_data = export_graphviz(clf,out_file=None, # feature_names=f_names, # class_names=["NL","L"], # filled=True,rounded=True,special_characters=True) # graph = pydotplus.graph_from_dot_data(dot_data) # graph.write_pdf("df_tree.pdf")
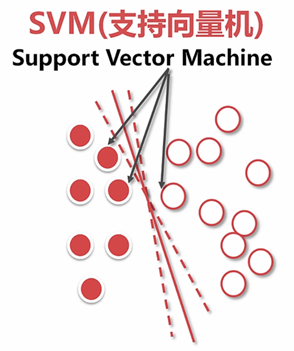
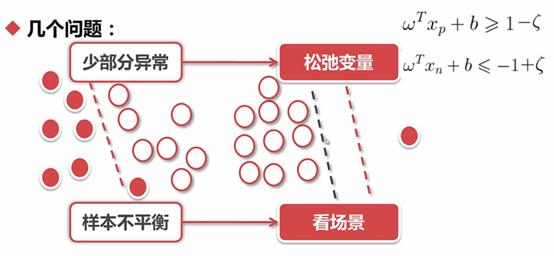
6.1.4 支持向量机



扩维:

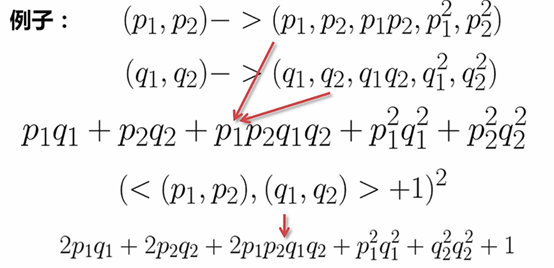

常用核函数:
线性核函数:线性可分用线性核函数
多项式核函数:若d =2,扩到19维;d=3,扩到19维;
RBF核函数:可以将空间映射为无限维

松弛变量的引入:
为了达到一个更宽的分界线,可以容忍少量的错分点,可以解决过拟合的问题
https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC
from sklearn.svm import SVC
#错分点的惩罚度设置的很大,有利于分类效果,通过C设置分类准备性
#C=1是的效果比KNN、GaussianNB、BernoulliNB、DecisionTreeClassifier的效果差很多
models.append(('SVM Classifier',SVC(C=100000)))
'''
0
SVM Classifier 准确率: 0.9756639626625181 召回率: 0.937984496124031 F1分数: 0.9494576505885068
1
SVM Classifier 准确率: 0.965 召回率: 0.9316493313521546 F1分数: 0.9227373068432672
2
SVM Classifier 准确率: 0.966 召回率: 0.9120567375886525 F1分数: 0.9265129682997119
'''
6.2 分类-集成
6.2.1 随机森林
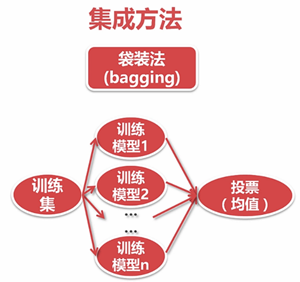
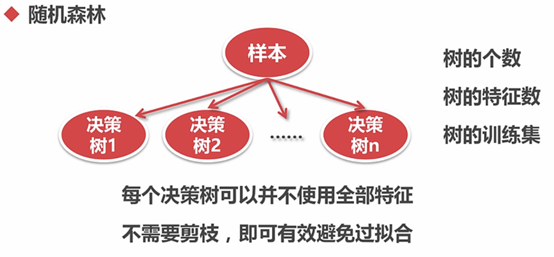
随机森林中的随机可以认为是每棵树训练集样本的随机、或者是没课数特征的随机、或者特征和样本来那个方面的随机。
models.append(('RandomForestClassifier默认', RandomForestClassifier()))
#If max_features is None, then max_features=n_features.
#Whether bootstrap samples are used when building trees. If False, the whole datset is used to build each tree.
#n_estimators的默认随机数为10,太多的随机数容易过拟合
models.append(('RandomForestClassifier有参',RandomForestClassifier(max_features=None,bootstrap=True,n_estimators=10)))
'''
0 ---: RandomForestClassifier默认 准确率: 0.9966662962551395 召回率: 0.9870069605568446 F1分数: 0.9929971988795518
1 ---: RandomForestClassifier默认 准确率: 0.9866666666666667 召回率: 0.9510791366906475 F1分数: 0.9706314243759178
2 ---: RandomForestClassifier默认 准确率: 0.9916666666666667 召回率: 0.9722607489597781 F1分数: 0.9824807288016819
0 ---: RandomForestClassifier有参 准确率: 0.9974441604622736 召回率: 0.9907192575406032 F1分数: 0.9946424411833217
1 ---: RandomForestClassifier有参 准确率: 0.983 召回率: 0.943884892086331 F1分数: 0.962582538517975
2 ---: RandomForestClassifier有参 准确率: 0.9886666666666667 召回率: 0.9667128987517337 F1分数: 0.9761904761904762
'''
结论:
bootstrap = True时效果比较好
效果比以上的分类器好,验证集的效果没有全用默认参数的好
调参时,一般比较验证集的结果
6.2.1 Adaboost
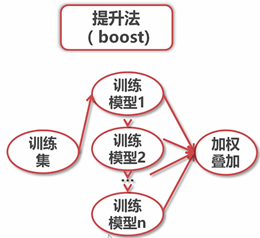

主要步骤:
1、首先给每个点赋一个初始的权值(不是给分类器赋权值)
2、循环一个弱分类器(所以一定会导致错分),将错分点相加得到
3、通过 得到分类器的权值
4、更新每个样本的权值,分对了乘以 (样本的权值会减小),分错了乘以 (样本的权值会增加)
说明:其中Z是正规权值话的参数,使所有的权值加起来还是为1
5、将每个分类器的权值 与结果相乘,再全部相加,得到最后的Adabosst的判别函数
例子:

Adaboost优点:
(1)精度高,且灵活可调
(2)几乎不用担心过拟合问题
(3)简化特征工程流程
from sklearn.ensemble import AdaBoostClassifier
#n_estimators表示提升终止的最大估计数,经验证n_estimators=10000时的效果和默认50想法效果差距不太大
models.append(('AdaBoostClassifier',AdaBoostClassifier(base_estimator=DecisionTreeClassifier(),n_estimators=10000)))
'''
0:训练集 1:验证集 2:测试集
0 ---: AdaBoostClassifier 准确率: 1.0 召回率: 1.0 F1分数: 1.0
1 ---: AdaBoostClassifier 准确率: 0.9753333333333334 召回率: 0.957037037037037 F1分数: 0.9458272327964862
2 ---: AdaBoostClassifier 准确率: 0.983 召回率: 0.9844192634560907 F1分数: 0.9646079111727968
'''
#需要注意base_estimator、n_estimators、algorithm、learning_rate这几个参数
6.3 回归
https://scikit-learn.org/stable/modules/model_evaluation.html


6.3.1 线性回归
回归分析是确定多个变量间相互依赖的定量关系的一种统计分析方法




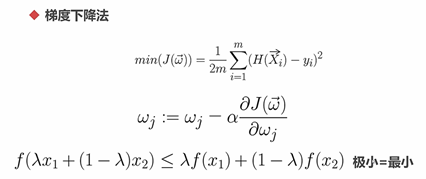
1、岭回归算法---Ridge()---惩罚回归函数的平方
本质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价,获得回归系数更符合实际、更可靠的回归方法。对病态数据的拟合要强于最小二乘法
2、套索回归算法---Lasso()---惩罚回归函数的绝对值
3、弹性网络回归算法---ElasticNet()
Ridge()和Lasso()的混合体
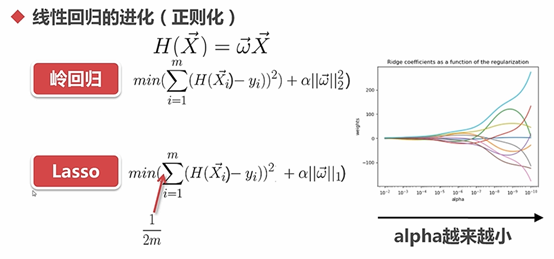


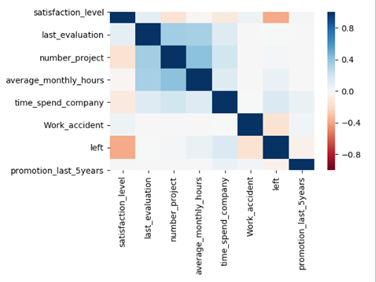
从上图中可以发现last_evaluation、number_project 、average_monthly_hours这3个属性相关性较强,使用这3个属性作为回归实验的属性。
def regre_test(features,label):
# print("X:",'\n',features)
# print("Y:",'\n',label)
#Ridge表示岭回归
from sklearn.linear_model import LinearRegression,Ridge,Lasso
# regr = LinearRegression()
# regr = Ridge(alpha=1) # alpha等于0时的效果与LinearRegression效果一样
regr = Lasso(alpha=0.0001)
regr.fit(features.values,label.values)
Y_pred = regr.predict(features.values)
print("Coef:",regr.coef_)
#用mean_squared_error衡量回归方程的好坏
from sklearn.metrics import mean_squared_error
print('MSE:',mean_squared_error(label.values,Y_pred))
def main():
features,label = hr_preprocessing()
regre_test(features[['number_project','average_monthly_hours']],features['last_evaluation'])
# hr_modeling(features,label)
'''
Coef: [0.27156879 0.26782676]
MSE: 0.05953825210281312
'''
#用这组数据中,用岭回归可以得到控制参数规模的作用,但是效果不是很明显
#用Lasso回归可以得到控制参数规模的作用,效果非常明显
6.3.2 逻辑回归
从本质上而言,是一种特殊的线性回归,是一种有形变的线性回归。
其值域为[0,1]。
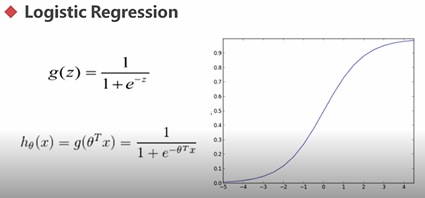
若将特征映射至高维,也可以用逻辑回归的思想来解决高维分类问题。
解析思路与线性回归思路是一致的。(结果发现效果并不理想)
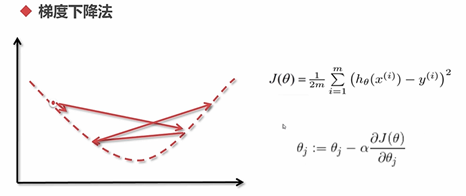
from sklearn.linear_model import LogisticRegression
#C越大,正则化的影响就越好,tol表示精度,solve表示所使用的算法(其中sag表示平均梯度下降算法 Stochastic Average Gradient descent solver)
#max_iter表示最大迭代次数
models.append(('LogisticRegression',LogisticRegression(C=1000,tol=1e-10,solver='sag',max_iter=10000)))
'''
0 ---- LogisticRegression 准备率: 0.7895321702411379 召回率: 0.3560429304713019 F1分数: 0.4461988304093567
1 ---- LogisticRegression 准备率: 0.799 召回率: 0.3279648609077599 F1分数: 0.4262607040913416
2 ---- LogisticRegression 准备率: 0.7813333333333333 召回率: 0.32483221476510066 F1分数: 0.4245614035087719
'''
效果一直很差,因为LogisticRegression()本质上还是一种线性的模型,此处所用的数据集不是线性可分的,所以所到的效果已经是在这种条件因素下最好的效果了。如果真要使线性回归达到比较理想的效果,解题思路应该参考SVM,将数据映射到高维空间中,使其线性可分.
6.3.3 人工神经网络
也是一个分类和回归都可以使用的模型
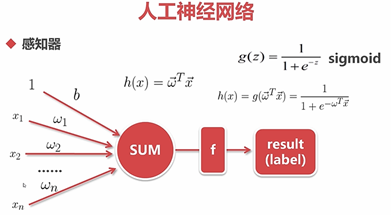
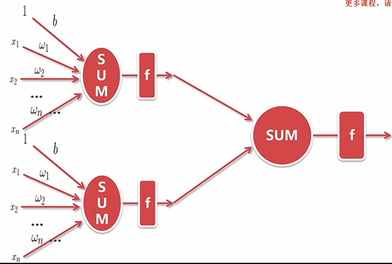


神经网络的优势:
可以将非线性拟合的很好,只要宽度足够大,深度足够深,神经网络可以拟合任何非线性的映射

Keras中文网站:
https://keras-cn.readthedocs.io/en/latest/other/objectives/
注意:随机梯度下降算法(sgd)及其变种亚当算法(adam)
#理解Sequential是人工神经网络的一个容器,该容器是一个序列化的
from keras.models import Sequential
#Dense是神经网络层,称为稠密层,Activation为激活函数
from keras.layers.core import Dense,Activation
#SGD是随机梯度下降算法
from keras.optimizers import SGD
mdl = Sequential()
mdl.add(Dense(units=50,input_dim=len(f_v[0])))#输入层
mdl.add(Activation('sigmoid'))
mdl.add(Dense(units=2))#输出层是标注,只有两个值,所对应的值的2
mdl.add(Activation('softmax'))#保证其归一化
sgd = SGD(lr=0.05)#构建一个优化器,lr表示学习率,相当于alpha
# from keras import losses
#编译建立模型,此时的loss相当于最优化函数,optimizer表示选用优化器函数
mdl.compile(loss="mse",optimizer="adam")#,adam优化器不仅考虑了梯度的作用,也考虑了动量的作用
#要求Y_train是One-Hot形式的,nb_epoch表示迭代的次数,batch_size表示随机梯度下降算法每次所选取的数量
mdl.fit(X_train,np.array([[0,1] if i==1 else [1,0] for i in Y_train]),nb_epoch=20000,batch_size=8999)
xy_lst = [(X_train, Y_train), (X_validation, Y_validation), (X_test, Y_test)]
for i in range(len(xy_lst)):
X_part = xy_lst[i][0]
Y_part = xy_lst[i][1]
Y_pred = mdl.predict_classes(X_part)#用predict()时输出的是连续值,使用predict_classes()时输出的是分类标注
# print(i)
from sklearn.metrics import accuracy_score, recall_score, f1_score
print(i, '---:', 'Nural Network', '准确率:', accuracy_score(Y_part, Y_pred),
'召回率:', recall_score(Y_part, Y_pred),
'F1分数:', f1_score(Y_part, Y_pred))
return
'''lr=0.01,optimizer=sgd,nb_epoch=1000,batch_size=2048时的结果
0 ---: Nural Network 准确率: 0.7647516390710078 召回率: 0.0 F1分数: 0.0
1 ---: Nural Network 准确率: 0.7616666666666667 召回率: 0.0 F1分数: 0.0
2 ---: Nural Network 准确率: 0.7536666666666667 召回率: 0.0 F1分数: 0.0
lr=0.05,optimizer=sgd,nb_epoch=20000,batch_size=8999,时的结果
0 ---: Nural Network 准确率: 0.8270918990999 召回率: 0.5118613138686131 F1分数: 0.5905263157894737
1 ---: Nural Network 准确率: 0.853 召回率: 0.5733532934131736 F1分数: 0.6346313173156587
2 ---: Nural Network 准确率: 0.843 召回率: 0.5414908579465542 F1分数: 0.620467365028203
lr=0.05,optimizer="adam",nb_epoch=20000,batch_size=8999,时的结果
0 ---: Nural Network 准确率: 0.9824424936104011 召回率: 0.931679925128685 F1分数: 0.9618357487922705
1 ---: Nural Network 准确率: 0.9736666666666667 召回率: 0.9205020920502092 F1分数: 0.9435310936383131
2 ---: Nural Network 准确率: 0.9703333333333334 召回率: 0.9093444909344491 F1分数: 0.9361091170136395
'''
召回率为0表示全部拟合成1个函数,未能拟合到真实函数,loss的值越小,表示拟合的效果越好,可调整参数nb_epoch、batch_size优化器的学习率lr
可以看到召回率有变化,证明学习正确了,但是学习率不能取很大,否则有可能不能很好的拟合数据
6.3.4 回归树与提升树
回归树(应用较少)
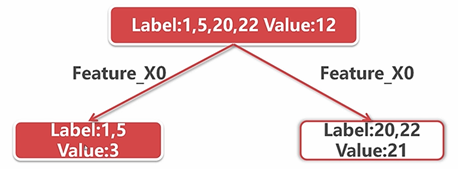
根据某一个特征进行切分,一定要满足在切分后的两部分的方差的和最小。
此时的label还是上一步取下来的值
提升树:基于回归树的集成方法(应用较多),尤其是梯度提升决策树效果最佳(根据差分值进行回归分析,直到将差分值变得越来越小)
此时的label值为上一步预测后的值与原来值的差分值。
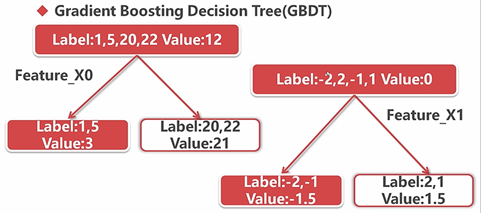

其中:Loss Function表示的是一棵树的loss
GBDT的算法:

特征数量较大的时候用GBDT的效果是比较好的。
from sklearn.ensemble import GradientBoostingClassifier
models.append(('GBDT',GradientBoostingClassifier(max_depth=6,n_estimators=100)))
'''
0:训练集 1:验证集 2:测试集
0 ---: GBDT 准确率: 0.9937770863429269 召回率: 0.9770114942528736 F1分数: 0.9869948908499767
1 ---: GBDT 准确率: 0.9893333333333333 召回率: 0.9645390070921985 F1分数: 0.9770114942528736
2 ---: GBDT 准确率: 0.9873333333333333 召回率: 0.9551374819102749 F1分数: 0.972017673048601
'''
6.4 聚类

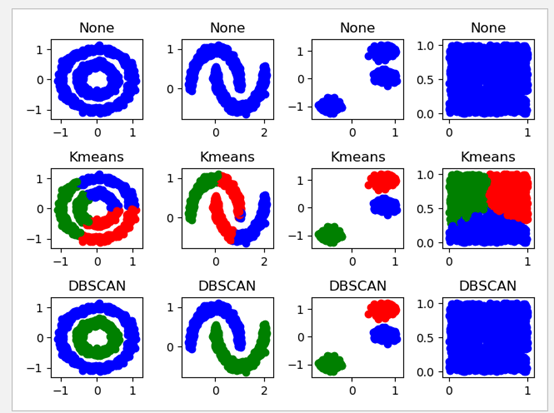
6.4.1 Kmeans

1、中心如何定义:取数据各个维度的均值
2、定义如何衡量:使用欧氏距离



https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html#sklearn.cluster.KMeans
import numpy as np
import matplotlib.pyplot as plt
#make_circles,make_blobs,make_moons可以制造一些点以供使用
from sklearn.datasets import make_circles,make_blobs,make_moons
from sklearn.cluster import KMeans
n_samples = 1000
#构造样本点
#n_samples表示构造样本点的个数,噪声的比例为0.05
circles = make_circles(n_samples = n_samples,factor=0.5,noise=0.05)
moons = make_moons(n_samples = n_samples,noise=0.05)
#指定random_state的目的是是的每次产生的blobs都是一样的,以免发生位置上的变化
blobs = make_blobs(n_samples = n_samples,random_state=8)
random_data = np.random.rand(n_samples,2),None #生成一个2维的,None是值得标注只占位置而不进行使用
# print(random_data)
#制定要用到的色系
colors = "bgrcmyk"
data = [circles,moons,blobs,random_data]
# print(data)
models =[]
#此时首先假设的模型并没有实体,Kmeans中的n_clusters=2表示被分为2类
models.append(("None",None))
models.append(("Kmeans",KMeans(n_clusters=2)))
f = plt.figure()
for inx,clt in enumerate(models):
clt_name,clt_entity = clt #clt分为两部分,第一部分是名字,第二部分是实体
#在没有聚类之前,认为所有的点都是同一个类
for i,dataset in enumerate(data):
X,Y = dataset
if not clt_entity: #如果实体为空
clt_res = [0 for item in range(len(X))] #没有聚类前认为其标注都是0
else:
clt_entity.fit(X)
#拟合(聚类)完成后,将得到的labels转化成int格式
clt_res = clt_entity.labels_.astype(np.int)
f.add_subplot(len(models),len(data),inx*len(data)+i+1)
plt.title(clt_name)
[plt.scatter(X[p,0],X[p,1],color=colors[clt_res[p]]) for p in range(len(X))]
plt.show()
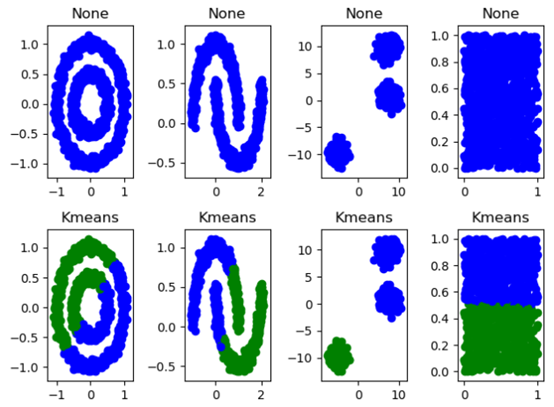


由结果可见:
切分方式是不同的,这是由于初始质心的选取所导致。
由于选择聚类为2类,所以看第2幅图第7个图可知,将最近的两个图案也当成一个类。
6.4.2 DBSCAN(基于密度)


DBSCAN算法的目的:找到密度相连对象的最大集合
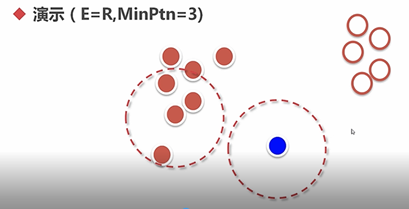
几个问题:
(1) 对离群点不敏感
(2) 需要kd-tree等数据结构辅助
(3) 需要先解决两个参数再使用DBSCAN
from sklearn.cluster import KMeans,DBSCAN
#指定random_state的目的是是的每次产生的blobs都是一样的,以免发生位置上的变化;
# center_box默认区间是(-10,10)
#cluster_std设置标准差,默认为1
blobs = make_blobs(n_samples = n_samples,random_state=8,center_box=(-1,1),cluster_std=0.1)
#eps表示E邻域,min_samples表示MinPtn
models.append(('DBSCAN',DBSCAN(min_samples=3,eps=0.2)))
在调参时,注意参数center_box、cluster_std、min_samples、eps
6.4.3 层次聚类

聚类过程是一层一层进行的,直到不能再聚为止
衡量方法采用距离衡量
A、最短距离:将两个簇最相近的两个点的距离作为簇间距离
B、最长距离:将两个簇最远的两个点的距离作为簇间距离
C、平均距离:将两个簇的中点见得距离违簇间距离
D、Ward: 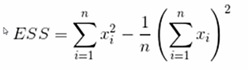
ESS增加的越大,越不将其合成一个簇,所以选定ESS增加较小的值作为下一步聚类的方法。
层次聚类的优点:聚类灵活
层次聚类的缺点:计算复杂度较高,离群点影响比较大

from sklearn.cluster import KMeans,DBSCAN,AgglomerativeClustering
#linkage表示使用的方法
models.append(('Agglomerative',AgglomerativeClustering(n_clusters=3,linkage='ward')))
虽然不一定能将相连的都分的很好,但是对于离散的群落,得到的结果和DBSCAN差不多。
6.4.4 图分裂

其中:
t表示承受系数, 表示分裂阈值(t> 时,应该将一条边或是一组边进行切分)
W1表示所选区域左边点的个数
W2表示所选区域右边点的个数
n表示将一个图分裂开所需要的边的个数
x表示最大连通图中边的数量
y表示最大连通图中点的个数
几个问题:
(1) 与层次聚类思路相反,为自顶向下
(2) 图建立方式、分裂方式可以非常灵活
6.5 关联
关联规则:反应一个事物与其它事物之间的相互依存性和关联性



提升度 > 1时表示购买X对购买Y起到了提升作用;
提升度 < 1 时表示购买X对购买Y并未提升作用,可以认为两者是相斥的,即购买了X将不会购买Y。
注意:
低阶频繁项集的组合可能是高阶频繁项集,也可能不是高阶级频繁项集;
低阶非频繁项集的组合一定是高阶非频繁项集;
低级频繁项集和低级非频繁项集的组合一定是高阶非频繁项集。


sklearn中不支持序列规则
6.6 半监督学习
样本集部分有标注,部分无标注。无标注的样本常远远大于有标注的样本。
目的:根据有标注的样本和样本的总体分布的情况给没有标注的样本进行标注。
6.6.1 标签传播算法
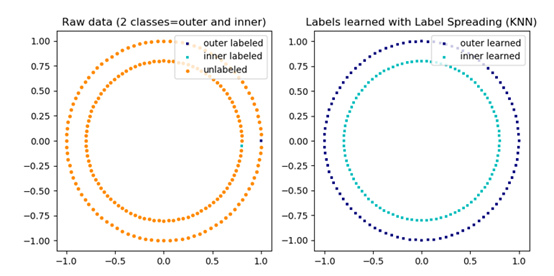
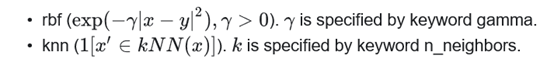
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
# print(iris)
labels = np.copy(iris.target)
# print(labels)
#生成0到1之间的随机数
random_unlabeled_points =np.random.rand(len(iris.target))
#生成的随机数若小于0.3则返回True--1,否则返回False--0
random_unlabeled_points = random_unlabeled_points < 0.3
Y = labels[random_unlabeled_points]
#重置标签,将random_unlabeled_points中为True的数换成-1
labels[random_unlabeled_points] = -1
print("Unlabeled Number:",list(labels).count(-1))
from sklearn.semi_supervised import LabelPropagation
label_prop_model = LabelPropagation()
label_prop_model.fit(iris.data,labels)
Y_pred = label_prop_model.predict(iris.data)
#对标注为-1的部分再预测一遍
Y_pred = Y_pred[random_unlabeled_points]
from sklearn.metrics import accuracy_score,recall_score,f1_score
print("准确率:",accuracy_score(Y,Y_pred))
print("召回率:",recall_score(Y,Y_pred,average='micro'))
print("f1分数:",f1_score(Y,Y_pred,average='micro'))
'''
Unlabeled Number: 45
准确率: 0.9555555555555556
召回率: 0.9555555555555556
f1分数: 0.9555555555555556
'''

关于模型的选用:可参考sklearn官网:
https://scikit-learn.org/stable/tutorial/index.html
https://scikit-learn.org/stable/tutorial/machine_learning_map/index.html