第4章 探索性数据分析（多因子与复合分析）

4.1、多因子

4.1.1 假设检验与方差检验

　　假设检验适用于（数据样本较小时）

　　方差检验适用于（数据样本较大时）

import numpy as np
import scipy.stats as ss
#生成一20个数的标准正态分布
norm_dist = ss.norm.rvs(size=20)
#检测norm_dist是否是正态分布，使用的方法是基于峰度和偏度的
print(ss.normaltest(norm_dist))

#结果：NormaltestResult(statistic=0.2025598777545946, pvalue=0.9036800223028876)
     #第一个是统计值，第二个值是p值

（1）P分布检验常用于比较两种样本是否一致（例如：临床医疗上药物是否有效）；

（2）独立分布t检验用于检测两组值的均值是都有比较大的差异性

print(ss.ttest_ind(ss.norm.rvs(size=10),ss.norm.rvs(size=20)))
#结果：Ttest_indResult(statistic=-0.575484958550556, pvalue=0.5695598474341583)

　　由于p值大于0.05（假定），可以接受该假设

（3）卡方检验常常用于确定两因素件是否有比较强的联系

import scipy.stats as ss
print(ss.chi2_contingency([[15,95],[85,5]]))
#结果：(126.08080808080808, 2.9521414005078985e-29, 1, array([[55., 55.],[45., 45.]]))
     #第一个值为卡方值，第二个值为P值，第三个值为自由度，第四个为与原数据数组同维度的对应理论值

　由于p值小于0.05（假定），拒绝该假设

（4）F检验常用于方差分析

　　　检测统计量F，做假设检验【F满足自由度（m-1，n-m）的F分布】

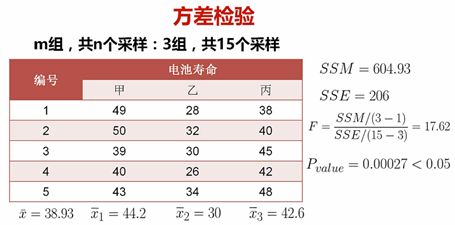
SST：总变差平方和

SSM：平均平方和（组间平方和）

SSE：残差平方和（组内平方和）

print(ss.f_oneway([49,50,39,40,43],[28,32,30,26,34,],[38,40,45,42,48]))
#结果：F_onewayResult(statistic=17.619417475728156, pvalue=0.0002687153079821641)

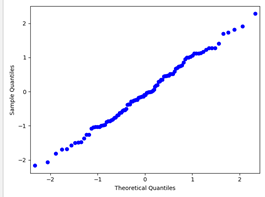
（5）使用qq图来对比一个分布是否属于一个已知的分布

  　　　方法：看散点图的是否在x，y轴的角平分线上

from statsmodels.graphics.api import qqplot
import matplotlib.pyplot as plt
qqplot(ss.norm.rvs(size=100))
plt.show()

 

4.1.2 相关系数

范围在[-1,1]----皮尔逊、斯皮尔曼（只与名次差有关，与具体数值相关性不强，故适用于相对比较的情况下）

　　衡量两组数据（或者两组样本）的分布趋势、变化趋势、一致趋势程度的因子，分为正相关（正向同步），负相关（反向同步）等。

　　　　其中：分子是协方差，分母是x，y的标准差，两者相乘相当于一个归一化因子

 

　　　　其中：n表示每组数据的数量，d值得是两组数据排名后的名次差

import pandas as pd
x = pd.Series([2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1])
y = pd.Series([2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9])
data = pd.DataFrame({'x':x,'y':y})
print('data:','\n',data)
print('Pearson相关系数：',x.corr(y))
print('Spearman相关系数：',x.corr(y,method='spearman'))
#Pearson相关系数： 0.9259292726922455
#Spearman相关系数： 0.9179373709568976

#DataFrame是针对于列进行相关性计算的，故需要对其进行转置
df = pd.DataFrame(np.array([x,y]).T)
print(df.corr())
'''结果
          0         1
0  1.000000  0.925929
1  0.925929  1.000000
'''

4.1.3 回归

线性回归

　　线性回归最常用的是解法：最小二乘法，其本质是最小化误差平方

 

线性回归效果判定的关键指标：

　　决定系数越接近于1说明效果越好；

　　DW的范围在【0 , 4】，DW=2时表示残差不相关，接近于4表示正相关，接近于0表示残差负相关，好的回归一般残差是不相关的。

  其中决定系数中的左R²：一元决定系数的定义；

　　　　　　　　 右R²：多元决定系数的定义；

　　　　　　　　　k：参数的个数

　　　　　　　　　e：残差（预测值与实际值的差）

https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression

import numpy as np
import scipy.stats as ss

x = np.arange(10).astype(np.float).reshape((10,1))
y =x*3+4+np.random.random((10,1))
print('实际值：','\n',y)
from sklearn.linear_model import LinearRegression
reg = LinearRegression()
res = reg.fit(x,y)
y_pre = reg.predict(x)
print('预测值：','\n',y_pre)
score = reg.score(x,y)
print('效果：',score)
a = reg.coef_
b = reg.intercept_
print('參數：',a,';截距：',b)
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(10,8))
plt.plot(x,y)
plt.plot(x,y_pre)
plt.show()

　　

4.1.4 主成分分析（PCA）与奇异值分解（SVD）

主成分分析（PCA）步骤

·         求特征协方差矩阵

·         求协方差的特征值和特征向量

·         将特征值从大到小排序，选择其中最大的k个

·         将样本点投影到选取的特征向量上

https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html#examples-using-sklearn-decomposition-pca

自写版本（按照PCA步骤）：

　　特别说明：np.linalg.eig(cov)之后的特征向量已按照对应的特征值从大至小进行排列

　　numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等
    　　eigvals函数可以计算矩阵的特征值，而eig函数可以返回一个包含特征值和对应的特征向量的元组

 #-----特别说明：np.linalg.eig(cov)之后的特征向量已按照对应的特征值从大至小进行排列
import numpy as np
import pandas as pd
x=[2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]
y=[2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9]
data = pd.DataFrame({'x':x,'y':y})
print('data:','\n',data)
cov = data.cov()
print('协方差矩阵:','\n',cov)
#求协方差矩阵的特征值和特征向量
#numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等
    #eigvals函数可以计算矩阵的特征值，而eig函数可以返回一个包含特征值和对应的特征向量的元组
eigen = np.linalg.eig(cov)
print(eigen)
eigenvalues = eigen[0]
print('eigenvalues:','\n',eigen[0])
#选取比较大的特征值所代表的特征向量
eigenvectors = eigen[1]
print('选取的特征值:','\n',eigen[0][1])
print('选取的特征向量:','\n',eigen[1][0])
jian = data-np.mean(data)
pcavectors = np.dot(jian,eigen[1][0])
print('主成分分析后的向量','\n',pcavectors)

 自写版本（使用函数按照PCA步骤）：

import numpy as np
import pandas as pd
def myPCA(data,n_components =1000000000):
    mean_vals = np.mean(data,axis=0)
    mid = data - mean_vals
    #此处需要针对列进行协方差计算
    cov_mat = np.cov(mid,rowvar=False)#rowvar默认为True，即对行求协方差
    from scipy import linalg
    eig_vals,eig_vects = linalg.eig(np.mat(cov_mat))
    #取出最大的特征值所对应的特征向量
    eig_val_index = np.argsort(eig_vals)#argsort()得到排序之后的索引
    eig_val_index = eig_val_index[:-(n_components+1):-1]
    eig_vects = eig_vects[:,eig_val_index]
    low_dim_mat = np.dot(mid,eig_vects)
    return low_dim_mat,eig_vals
x=[2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]
y=[2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9]
data = pd.DataFrame([x,y]).T
print(myPCA(data,n_components=1))

接口版本：

from sklearn.decomposition import PCA
import numpy as np
import pandas as pd
x=[2.5,0.5,2.2,1.9,3.1,2.3,2,1,1.5,1.1]
y=[2.4,0.7,2.9,2.2,3.0,2.7,1.6,1.1,1.6,0.9]
data = pd.DataFrame([x,y]).T
#降维
lower_dim = PCA(n_components=1)  #降为1维
new = lower_dim.fit(data)
print(new)
　　#PCA(copy=True, iterated_power='auto', n_components=1, random_state=None,
　　#svd_solver='auto', tol=0.0, whiten=False)
　　#copy如果为False，则传递给fit的数据将被覆盖并且运行fit（X）.t
important = lower_dim.explained_variance_ratio_
print(important)  #[0.96318131],说明得到了96.3%的信息量
newdata = lower_dim.transform(data)
print(newdata)    #转化后的数值

注意：sklearn中所用到的PCA方法是奇异值分解（SVD），与上述PCA的步骤不一样，所以两者所得出的结论会有些许不同

4.2、复合分析

4.2.1交叉分析

　　除了纵向分析横向分析外，可以使用交叉分析来分析数据属性和属性的关系

sns.heatmap()用于做热图-----两个不同属性间相互影响的情况！

import numpy as np
import pandas as pd
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv("HR.csv")
##查看各个部门的离职之间是否有明显差异----使用独立t检验方法
    ##得到各个部门的离职分布

#得到分组后的索引值
dp_indices = df.groupby(by = 'department').indices
# print(dp_indices)
sales_values = df["left"].iloc[dp_indices['sales']].values
technical_values = df["left"].iloc[dp_indices['technical']].values
print(ss.ttest_ind(sales_values,technical_values))

#求两两部门间的p值
dp_keys = list(dp_indices.keys())
print(dp_keys)
dp_t_mat = np.zeros([len(dp_keys),len(dp_keys)])
for i in range(len(dp_keys)):
    for j in range(len(dp_keys)):
        p_values = ss.ttest_ind(df['left'].iloc[dp_indices[dp_keys[i]]].values,
                                df['left'].iloc[dp_indices[dp_keys[j]]].values)[1]
        if p_values<0.05:
            dp_t_mat[i][j] = -1
        else:
            dp_t_mat[i][j] = p_values
sns.heatmap(dp_t_mat,xticklabels=dp_keys,yticklabels=dp_keys)
plt.show()
#只有为黑色的，两个部门的才有显著性差异

 

# 采用透视表
piv_tb = pd.pivot_table(df,values='left',index=['promotion_last_5years','salary'],
                        columns=['Work_accident'],aggfunc=np.mean)
print(piv_tb)
sns.heatmap(piv_tb,vmin=0,vmax=1,cmap=sns.color_palette("Reds",n_colors=256))#指定最大值为1，最小值为0
plt.show()

颜色越深，离职率越高

4.2.2分组与钻取

钻取是改变数据维度层次，变换分析粒度的过程，可分为向下和向上钻取。
连续属性在分组前需要进行离散化。
连续分组：

·         分割（一阶差分）、拐点（二阶差分）

·         聚类

·         不纯度（Gini系数）

#求Gini系数
s1 = pd.Series(['X1','X1','X2','X2','X2'])
s2 = pd.Series(['Y1','Y1','Y1','Y2','Y2'])
#求平方和：
def getProbSS(s):
    if type(s)!= pd.core.series.Series:
        s = pd.Series(s)
    prt_ary = s.groupby(by=s).count().values/float(len(s))
    return 1- sum(prt_ary**2)
def getGini(s1,s2):
    d = dict()
    for i in list(range(len(s1))):
        d[s1[i]] = d.get(s1[i], []) + [s2[i]]
    return 1 - sum([getProbSS(d[k]) * len(d[k])/float(len(s1)) for k in d])
print("Gini:",getGini(s1,s2))
#结果：Gini: 0.7333333333333334

　

sns.barplot(x='salary',y='left',hue='department',data=df)
plt.show()

#拐点（二阶差分）
sl_s = df['satisfaction_level']
sns.barplot(list(range(len(sl_s))),sl_s.sort_values())
plt.show()

4.2.3相关分析

#heatmap()会自动屏蔽离散化信息。例如，salary有low、medium、high

sns.heatmap(df.corr(),vmin=-1,vmax=1,cmap=sns.color_palette("RdBu",n_colors=128))
plt.show()

对离散属性相关性的处理：

　　利用熵来进行离散属性相关性的计算

        　　熵：用于衡量不确定性，条件熵不具有对称性

 

s1 = pd.Series(['X1','X1','X2','X2','X2','X2'])
s2 = pd.Series(['Y1','Y1','Y1','Y2','Y2','Y2'])
def getEntropy(s):
    if type(s)!= pd.core.series.Series:
        s = pd.Series(s)
    prt_ary = s.groupby(by=s).count().values/float(len(s))
    return (-(np.log2(prt_ary))*prt_ary).sum()
#条件熵需要注意
def getCondEntropy(s1,s2):#s1条件下s2的熵
    d = dict()
    for i in list(range(len(s1))):
        d[s1[i]] = d.get(s1[i],[])+[s2[i]]
        #{'X1': ['Y1', 'Y1'], 'X2': ['Y1', 'Y2', 'Y2', 'Y2']}
    return sum([getEntropy(d[k]) * len(d[k])/float(len(s1)) for k in d])
def getEntropyGain(s1,s2):
    return (getEntropy(s2) - getCondEntropy(s1,s2))
def getEntropyGainRatio(s1,s2):
    return getEntropyGain(s1,s2)/getEntropy(s2)
import math
def getCoor(s1,s2):
    return getEntropyGain(s1,s2)/math.sqrt(getEntropy(s1)*getEntropy(s2))
print('熵:',getEntropy(s2))
print('条件熵:',getCondEntropy(s1,s2))
print('熵增益:',getEntropyGain(s1,s2))
print('熵增益率:',getEntropyGainRatio(s2,s1))
print('相关性:',getCoor(s1,s2))
'''
结果：
熵: 1.0
条件熵: 0.5408520829727552
熵增益: 0.4591479170272448
熵增益率: 0.5
相关性: 0.4791387674918639
'''

4.2.4因子分析

　　探索性因子分析：通过协方差矩阵、相关性矩阵等指标分析多元属性变量的本质结构，并可以进行转化、降维等操作，得到影响目标属性的最主要因子。

　　验证性因子分析：验证一个因子与关注的属性之间是否有一定的关联，有何关联。

 

from sklearn.decomposition import PCA
my_pca = PCA(n_components=7)
#拟合时不允许出现离散型数据，drop默认情况下从行进行删除
low_mat = my_pca.fit_transform(df.drop(labels=['salary','department','left'],axis=1))
#通过PCA降维后信息的准确性
print("Ratio:",my_pca.explained_variance_ratio_)
sns.heatmap(pd.DataFrame(low_mat).corr(),vmin=-1,vmax=1,cmap = sns.color_palette("RdBu",n_colors=128))
plt.show()
#结果：Ratio: [9.98565340e-01 8.69246970e-04 4.73865973e-04 4.96932182e-05 2.43172315e-05 9.29496619e-06 8.24128218e-06]

通过PCA，将原来的特征空间变成了一个正交的特征空间

4.2.5聚类分析、回归分析（暂略）

可参考作者另一篇作文【面试问题汇总 - 大脸猫12581 - 博客园 (cnblogs.com)第7部分与第8部分】