How we implemented consistent hashing efficiently
翻译自
https://medium.com/ably-realtime/how-to-implement-consistent-hashing-efficiently-fe038d59fff2
我们如何有效地实现一致的哈希
Ably的实时平台分布在14个以上的物理数据中心和100多个节点中。为了确保负载和数据在所有节点上均匀一致地分布,我们使用一致的哈希算法。
在本文中,我们将了解什么是一致性哈希,以及为什么它是可伸缩分布式系统体系结构中必不可少的工具。此外,我们将研究可用于大规模有效实现此算法的数据结构。最后,我们还将看一个相同的工作示例。
再谈散列
还记得您在大学期间学到的旧式哈希处理方法吗?使用哈希函数,我们确保计算机程序所需的资源可以有效地存储在内存中,从而确保内存中的数据结构被均匀加载。我们还确保了这种资源存储策略也使信息检索更加有效,从而使程序运行更快。
经典的散列方法使用散列函数来生成伪随机数,然后将其除以存储空间的大小,以将随机标识符转换为可用空间内的位置。类似于以下内容:
location = hash(key) mod size
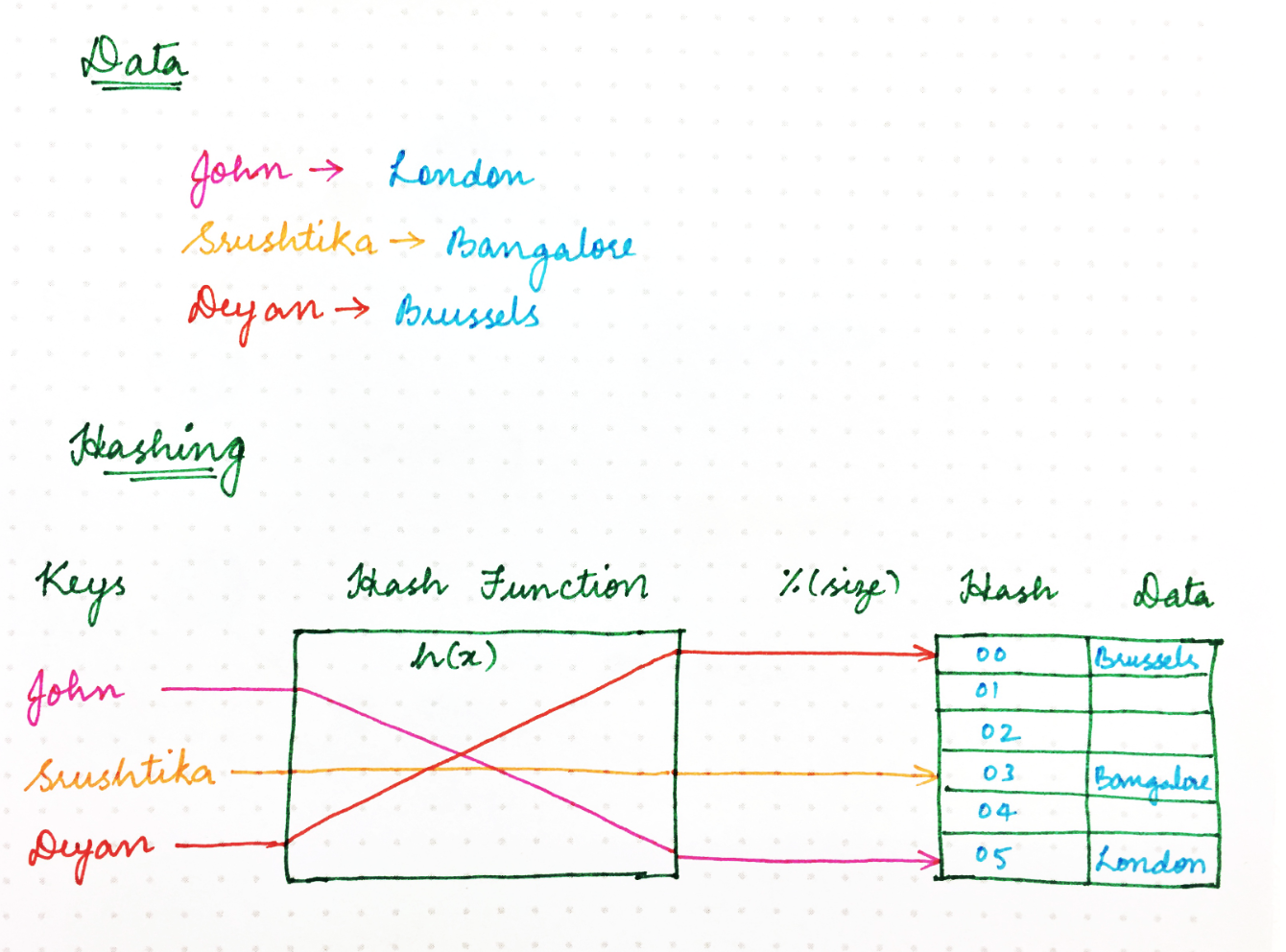
那么,为什么我们不能使用相同的方法来处理网络上的请求呢?
在各种程序,计算机或用户正在从多个服务器节点请求某些资源的情况下,我们需要一种将请求均匀地映射到可用服务器节点的机制,从而确保负载平衡并可以保持一致的性能。我们可以将服务器节点视为一个或多个请求可以映射到的占位符。
现在让我们退后一步。在经典的哈希方法中,我们始终假设:
- 内存位置的数量是已知的,并且
- 这个数字永远不会改变。
例如,在Ably,我们通常会一天一整天地放大和缩小群集大小,并且还必须应对意外故障。但是,如果考虑上述情况,则不能保证服务器节点的数量将保持不变。如果其中之一意外失败怎么办?使用幼稚的哈希方法,我们最终将需要重新哈希每个键,因为新的映射取决于节点/内存位置的数量,如下所示:
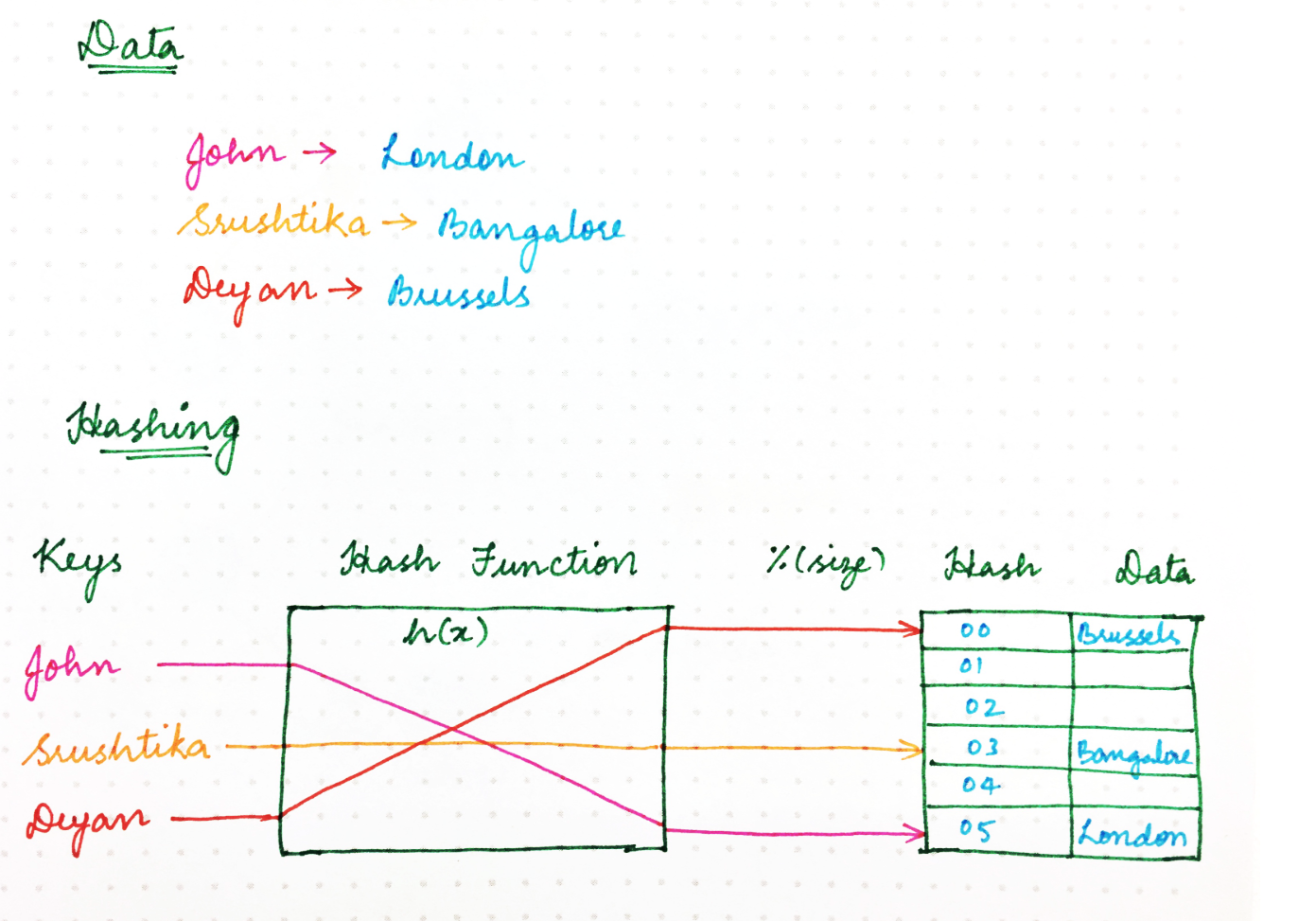
before

afther
在具有简单哈希值(每个键的位置都在其中移动)的分布式系统中,问题在于每个节点上都存储有状态。例如,集群大小的微小变化可能会导致大量工作需要重新调整集群周围的所有数据。随着群集大小的增长,这变得不可持续,因为每个哈希更改所需的工作量随群集大小线性增长。这就是一致性哈希的概念出现的地方。
一致的哈希?
一致性哈希可以描述如下:
- 它以某种虚拟环结构(称为散列)的形式表示资源请求者(就本博客而言,我们将从现在起将其称为“请求”)。
- 位置的数量不再固定,但是环被认为具有无限数量的点,并且服务器节点可以放置在该环上的随机位置。当然,可以使用哈希函数再次选择此随机数,但是跳过了将其除以可用位置数的第二步,因为它不再是有限数。
- 与经典哈希方法中的密钥类似的请求(即用户,计算机或无服务器程序)也使用相同的哈希函数放置在同一环上。

那么,如何决定哪个服务器节点将服务于哪个请求呢?如果我们假设环是有序的,则环的顺时针遍历与位置地址的递增顺序相对应,则每个请求都可以由首先出现在该顺时针遍历中的服务器节点来满足;也就是说,地址大于请求地址的第一个服务器节点将为其提供服务。如果请求的地址高于最高寻址节点,则该请求将由地址最小的服务器节点提供服务,因为通过环的遍历以循环方式进行。如下图所示:

从理论上讲,每个服务器节点“拥有”一个散列范围,并且在此范围内的所有请求都将由同一服务器节点服务。现在,如果这些服务器节点之一发生故障(例如节点3),下一个服务器节点的范围会扩大,并且所有请求都进入该范围,那么该请求将转到新的服务器节点。就是这样。只是该范围(对应于发生故障的服务器节点)需要重新分配,而其余的散列和请求节点分配仍然不受影响。这与经典的哈希技术相反,在经典的哈希技术中,哈希表大小的变化有效地干扰了所有映射。由于使用了一致的散列,给定的环更改将仅影响请求的一部分(相对于环分配因子)。(由于节点的添加或删除导致某些请求节点映射发生更改,因此发生了环更改。)

高效的实施方法
现在我们对哈希环是什么感到满意了……
我们需要实现以下内容才能使其正常工作:
- 从哈希空间到集群中节点的映射,使我们能够找到负责给定请求的节点。
- 那些对集群的请求解析为给定节点的集合。继续前进,这将使我们能够找出哪些哈希值受特定节点的添加或删除影响。
映射
为了完成上面的第一部分,我们需要以下内容:
- 给定请求标识符的哈希函数,用于计算环中的位置。
- 一种找出哪个节点对应于散列请求的方法。
为了找出与特定请求相对应的节点,我们可以使用一个简单的数据结构来表示它,包括以下内容:
- 对应于环中节点的哈希数组。
- 用于查找与特定请求相对应的节点的映射(哈希表)。
这本质上是有序映射的原始表示。
要在上述结构中找到负责给定哈希的节点,我们需要:
- 执行修改后的二进制搜索以查找数组中等于或大于您要查找的哈希(≥)的第一个节点哈希。
- 在地图中查找与找到的节点哈希相对应的节点
添加或删除节点
正如我们在本文开头所看到的,添加新节点时,必须将包含各种请求的哈希的某些部分分配给该节点。相反,当一个节点被删除时,已经分配给该节点的请求将需要由其他某个节点来处理。
我们如何找到那些受到环更改影响的请求?
一种解决方案是遍历分配给节点的所有请求。对于每个请求,我们都决定是否将其置于已发生的环更改的范围内,并在必要时将其移至其他位置。
但是,随着分配给给定节点的请求数量的扩展,执行此操作所需的工作也随之增加。随着节点数量的增加环发生变化的数量趋于增加,情况变得更糟。在最坏的情况下,由于环的更换通常与局部故障有关,因此与环的更换相关的瞬时负载也可能增加其他受影响节点的可能性,从而可能导致整个系统级联的问题。
为了解决这个问题,我们希望重新分配请求尽可能地高效。理想情况下,我们会将所有请求存储在一个数据结构中,该数据结构使我们能够找到在环上任何位置受单个哈希更改影响的请求
有效查找受影响的哈希
从群集中添加或删除节点将更改环的某些部分中的请求分配,我们将其称为受影响范围。如果我们知道受影响范围的边界,我们将能够将请求移至正确的位置。
为了找到受影响范围的边界,从添加或删除的节点的哈希H开始,我们可以从H绕环向后(图中的逆时针方向)移动,直到找到另一个节点。让我们称该节点S的哈希为开始。该节点的逆时针方向的请求将位于该节点上,因此它们不会受到影响。
请注意,这是对所发生情况的简化描述。实际上,由于我们使用大于1的复制因子和专门的复制策略,在该结构和算法中,节点和子集仅适用于任何给定请求,因此结构和算法更加复杂。
在找到的节点与已添加(或删除)的节点之间的范围内具有放置哈希值的请求是那些需要移动的请求。
在受影响的范围内有效查找请求
一种解决方案是简单地遍历与节点相对应的所有请求,并更新具有该范围内的哈希值的那些请求。
在JavaScript中,可能看起来像这样:
for (const request of requests) { if (contains(S, H, request.hash)) { /* the request is affected by the change */ request.relocate(); } } function contains(lowerBound, upperBound, hash) { const wrapsOver = upperBound < lowerBound; const aboveLower = hash >= lowerBound; const belowUpper = upperBound >= hash; if (wrapsOver) { return aboveLower || belowUpper; } else { return aboveLower && belowUpper; } }
由于环是圆形的,仅查找S <= r <H的请求是不够的,因为S可能大于H(意味着范围环绕环的顶部)。该函数contains()处理这种情况。
只要请求的数量相对较少,或者在节点的添加或删除相对很少的情况下,遍历给定节点上的所有请求就可以了。
但是,随着给定节点上请求数量的增加,所需的工作也会增加,而且更糟糕的是,随着节点数量的增加,环的更改往往会更频繁地发生,无论是由于自动缩放还是由于故障转移,都会触发整个系统的同时负载以重新平衡请求。
在最坏的情况下,与此相关的负载可能会增加其他节点发生故障的可能性,从而可能导致整个系统级联的问题。
为了减轻这种情况,我们还可以将请求存储在一个单独的环形数据结构中,该结构类似于前面讨论的结构。在此环中,哈希直接映射到位于该哈希处的请求。
然后,我们可以通过执行以下操作找到一个范围内的请求:
- 在范围的起点S之后找到第一个请求。
- 顺时针迭代,直到找到哈希范围之外的请求。
- 重新定位范围内的那些请求。
对于给定的哈希更新,需要迭代的请求数平均为R / N,其中R是位于节点范围内的请求数,N是环中的哈希数(假设分布均匀)的请求。
让我们通过一个有效的示例将上述解释付诸实践:
假设我们有一个包含两个节点A和B的集群。
让我们为这些节点中的每个节点随机生成一个“放置哈希” :(假设32位哈希),因此我们得到
A:0x5e6058e5
B:0xa2d65c0
其中数字的假想环上这个地方的节点0x0,0x1,0x2...被置于连续到0xffffffff,这是又卷曲应遵循的0x0。
由于节点A具有哈希值0x5e6058e5,因此它负责哈希范围从up到0xa2d65c0+1up的所有请求,如下所示:0xffffffff0x00x5e6058e5

B上的另一方面是负责的范围内0x5e6058e5+1可达0xa2d65c0。因此,整个散列空间被分布。
从节点到其哈希的映射需要与整个集群共享,以便环计算的结果始终相同。因此,任何需要特定请求的节点都可以确定它的位置
假设我们要查找(或创建)具有标识符“ bobs.blog@example.com”的请求。
- 我们计算标识符的哈希H,例如
0x89e04a0a - 我们看一下环,找到哈希大于H的第一个节点。这里恰好是B。
因此,B是负责该请求的节点。如果我们再次需要该请求,则将重复上述步骤并再次到达具有所需状态的同一节点上。
这个例子有点简单化了。实际上,每个节点只有一个散列可能很不公平地分配负载。您可能已经注意到,在此示例中,(0xa2d656c0-0x5e6058e5)/232 = 26.7%环网由B 负责,其余部分由A负责。理想地,每个节点将负责环的相等部分。
使这种公平的一种方法是为每个节点生成多个随机哈希,如下所示:

实际上,我们发现这样做的结果仍然不能令人满意,因此我们将环划分为64个相等大小的段,并确保每个节点的哈希都放置在每个段中的某个位置。但是,此细节并不重要。目的只是确保每个节点负责环的相等部分,以使负载均匀分布。(每个节点具有多个哈希的另一个优点是可以逐渐将哈希添加到环中或从环中删除,以避免负载突然增加。)
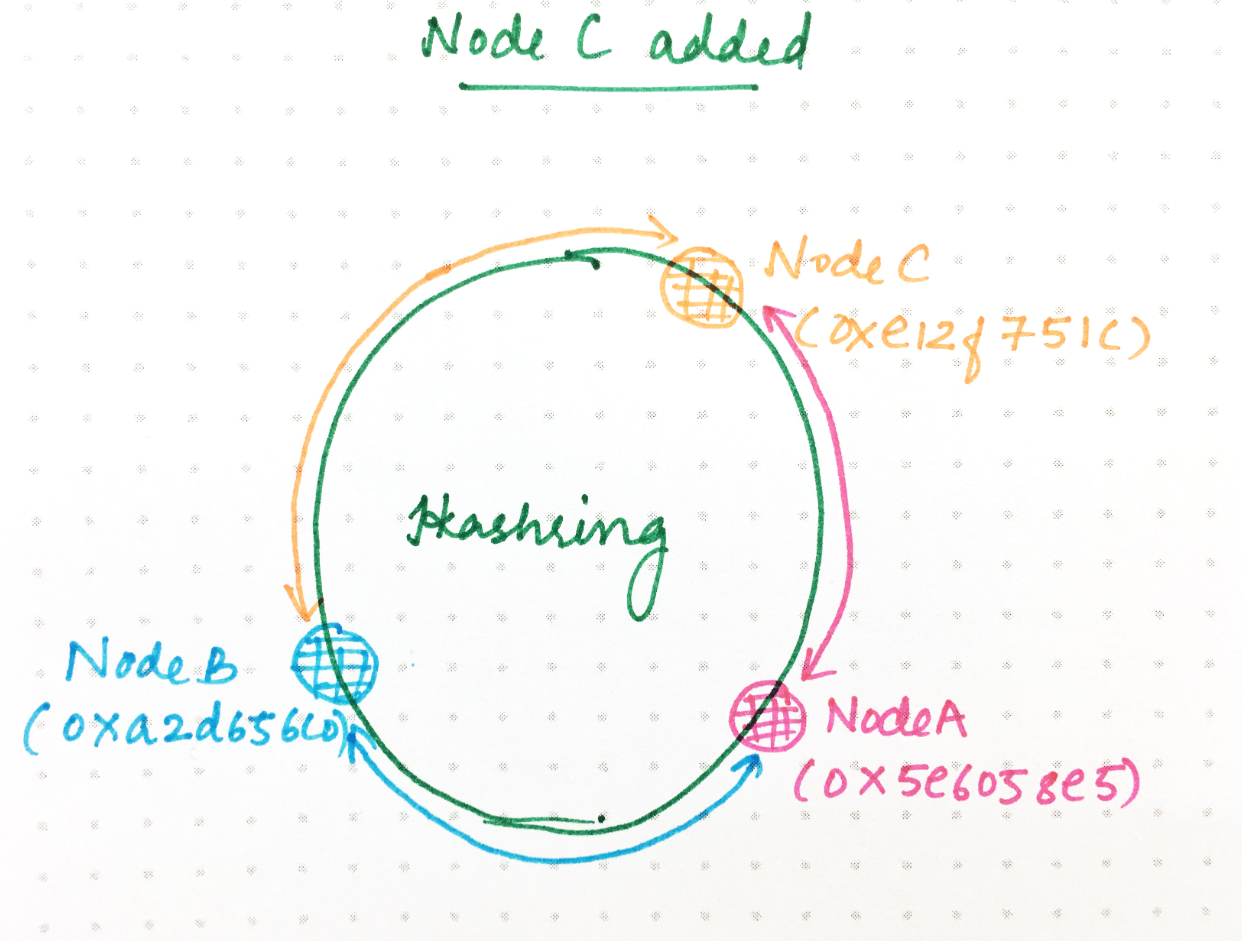
假设现在我们向该环添加一个名为C的新节点。我们为C生成一个随机哈希。
A:0x5e6058e5
B:0xa2d65c0
C:0xe12f751c
现在,0xa2d65c0 + 1和之间0xe12f751c(用于哈希到A的)之间的环形空间现在委托给C。所有其他请求将继续像以前一样哈希到同一节点。为了处理这种权力转移,A上已经存在的该范围内的所有请求都需要将其所有状态转移到C。
您现在了解了为什么在分布式系统中需要散列以平均分配负载。但是,需要进行一致的哈希处理,以确保在发生环更改时将群集中所需的工作量减至最少。
另外,节点需要存在于环上的多个位置,以确保统计上的负载更有可能更均匀地分布。对于每个环更改,迭代整个哈希环效率不高。随着分布式系统的扩展,必须有一种更有效的方法来确定更改的内容,以最大程度地减少环更改对性能的影响。需要新的索引和数据类型来解决此问题。
构建分布式系统很困难。我们喜欢它,也喜欢聊天。如果需要依靠,请使用Ably。如果您想聊天,请联系!
感谢Ably的分布式系统工程师John Diamond对本文的投入。



