KMP算法与next模式值求解的总结
最近在学习数据结构这门课,KMP算法在课堂上听得晕晕乎乎,百度谷歌搞了一下午,总算理清头绪了,现在总结如下,部分内容来自网上整理。
KMP字符串模式匹配详解
KMP字符串模式匹配就是一种在一个字符串中定位另一个字符串的高效算法。
简单匹配算法的时间复杂度为O(m*n);而KMP匹配算法,可以证明它的时间复杂度为O(m+n).。
一. 简单匹配算法
先来看一个简单匹配算法的函数:
int Index_BF ( char S [ ], char T [ ], int pos )
{
/* 若串 S 中从下标0≤pos<StrLength(S)的字符
起存在和串 T 相同的子串,则称匹配成功,返回第一个
这样的子串在串 S 中的下标,否则返回 -1 */
int i = pos, j = 0;
while ( S[i+j] != '\0'&& T[j] != '\0')
if ( S[i+j] == T[j] )
j ++; // 继续比较后一字符
else
{
i ++;
j = 0; // 重新开始新的一轮匹配
}
if ( T[j] == '\0')
return i; // 匹配成功 返回下标
else
return -1; // 串S中(第pos个字符起)不存在和串T相同的子串
} // Index_BF
此算法的思想是直截了当的:将主串S中某个位置i起始的子串和模式串T相比较。即从 j=0 起比较 S[i+j] 与 T[j],若相等,则在主串 S 中存在以i 为起始位置匹配成功的可能性,继续往后比较( j逐步增1 ),直至与T串中最后一个字符相等为止,否则改从S串的下一个字符起重新开始进行下一轮的"匹配",即将串T向后滑动一位,即 i 增1,而 j 退回至0,重新开始新一轮的匹配。
例如:在串S=”abcabcabdabba”中查找T=” abcabd”(我们可以假设从下标0开始):先是比较S[0]和T[0]是否相等,然后比较S[1]和T[1]是否相等…我们发现一直比较到S[5] 和T[5]才不等。如图:
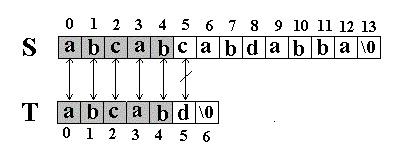
当这样一个失配发生时,T下标必须回溯到开始,S下标回溯的长度与T相同,然后S下标增1,然后再次比较。如图:
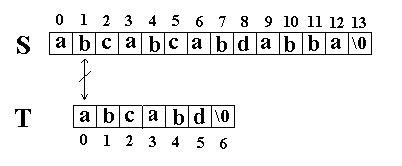
这次立刻发生了失配,T下标又回溯到开始,S下标增1,然后再次比较。如图:
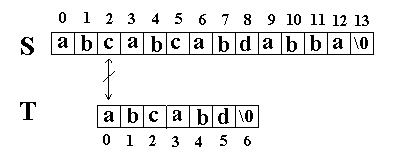
又一次发生了失配,所以T下标又回溯到开始,S下标增1,然后再次比较。这次T中的所有字符都和S中相应的字符匹配了。函数返回T在S中的起始下标3。如图: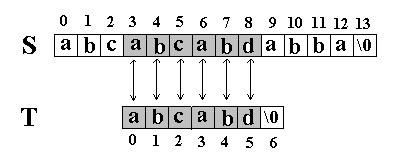
二. KMP匹配算法
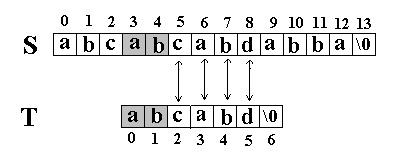
还是相同的例子,在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5] 和T[5]不等后,S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值(next[5]=2,理由后面讲),直接比较S[5] 和T[2]是否相等,因为相等,S和T的下标同时增加;因为又相等,S和T的下标又同时增加,最终在S中找到了T。如图:
KMP匹配算法和简单匹配算法效率比较,一个极端的例子是:
在S=“AAAAAA…AAB“(100个A)中查找T=”AAAAAAAAAB”, 简单匹配算法每次都是比较到T的结尾,发现字符不同,然后T的下标回溯到开始,S的下标也要回溯相同长度后增1,继续比较。如果使用KMP匹配算法,就不必回溯.
对于一般文稿中串的匹配,简单匹配算法的时间复杂度可降为O (m+n),因此在多数的实际应用场合下被应用。
KMP算法的核心思想是利用已经得到的部分匹配信息来进行后面的匹配过程。看前面的例子。为什么T[5]==’d’的模式函数值等于2(next[5]=2),其实这个2表示T[5]==’d’的前面有2个字符和开始的两个字符相同,且T[5]==’d’不等于开始的两个字符之后的第三个字符(T[2]=’c’).如图:
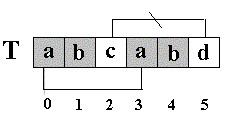
也就是说,如果开始的两个字符之后的第三个字符也为’d’,那么,尽管T[5]==’d’的前面有2个字符和开始的两个字符相同,T[5]==’d’的模式函数值也不为2,而是为0。
前面说:在S=”abcabcabdabba”中查找T=”abcabd”,如果使用KMP匹配算法,当第一次搜索到S[5] 和T[5]不等后,S下标不是回溯到1,T下标也不是回溯到开始,而是根据T中T[5]==’d’的模式函数值,直接比较S[5] 和T[2]是否相等。因为,S[4] ==T[4],S[3] ==T[3],根据next[5]=2,有T[3]==T[0],T[4] ==T[1],所以S[3]==T[0],S[4] ==T[1](两对相当于间接比较过了),因此,接下来比较S[5] 和T[2]是否相等。
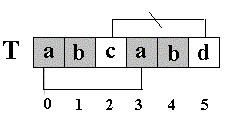
三. 怎么求串的模式值next[j]
next[j]值的含义:
-1:若S[i]!=T[j]产生失配,则下一次比较S[i+1]与T[0];
0:若S[i]!=T[j]产生失配,则下一次比较S[i]与T[0];
k:若S[i]!=T[j]产生失配,则下一次比较S[i]与T[k];
next[j]的求解思路(自己总结的,如有疏漏望大家指出)
1.next[0]=-1
2.j的前面的k个字符与开头的k个字符进行比较,若对应相等且T[k]==T[j]但T[k]!=T[0],则next[j]=0;
j的前面的k个字符与开头的k个字符进行比较,若对应相等且T[k]==T[j]但T[k]==T[0],则next[j]=-1;
j的前面的k个字符与开头的k个字符进行比较,若对应相等且T[k]!=T[j],则next[j]=k;
3.j的前面的k个字符与开头的k个字符进行比较,若不等且T[k]==T[0],则next[j]=-1;
j的前面的k个字符与开头的k个字符进行比较,若不等且T[k]!=T[0],则next[j]=0;
说明:其实上面这个只不过是个人总结抽象出来的求解方法,当真正理解透彻KMP算法的本质和目的,完全无视我的求解过程也是可以的,直接看一下就能计算出正确的next[j]的值了,只要记住next[j]只有-1,0,k三种情况,关键是搞清楚如何排除其他值,排除的依据是什么,而依据就是上面所述的算法原理。另外,博友可能会在其他书籍看到next[j]只有0,1,k的情况,实际上这个是根据数组下标决定的,next[j]只是数组下标的值,本文所用的数组下标是从0开始,而0,1,k这种取值是数组下标从1开始,为什么?请回去再想一想算法的原理吧。
另外,本文中的next[j]计算方法是最优的,也就是优化后的KMP算法,博友如果看到其他取值,除去数组下标不一致的可能性外,就是是否有优化的区别了。
思考题(我觉得比较典型的),大家可以尝试计算以下模式串中最后一个元素T[j]的next[j]值:
(1)abcabc k=2
(2)abaaba k=2
(3)abcabd、abcaba k=2
(4)abca k=0
(5)abcb k=0
提示:一定要想清楚T[k]、T[j]、T[0](即标红的元素)之间的关系对next[j]的影响!!!
答案:
(1)-1 0 0 -1 0 0
(2)-1 0 -1 1 0 -1
(3)-1 0 0 -1 0 2 、 -1 0 0 -1 0 2
(4)-1 0 0 -1
(5)-1 0 0 0
答案分析和原因综述:
当k!=0的时,也就是可以找出k个字符使T[0...k-1]==T[j-k...j-1],此时能判断出next[j]可能有k、0、-1三种情况,若再满足T[k]==T[j],就排除了next[j]=k的情况,以(1)举例来说,若T[j]产生失配,即S[i]!=T[j]产生失配,而当T[j]==T[k]时,必然有S[i]!=T[k],故排除next[j]=k的情况。此时next[j]还有0、-1两种可能,这两种的区别无非在于下一次比较是T[0]与S[i],还是T[0]与S[i+1],显而易见,若S[i]!=T[j]产生失配,而当T[0]==T[j],那么必然有S[i]!=T[0],因而直接进行T[0]与S[i+1]的比较就可以,也就是排除next[j]=0的情况,从而next[j]=-1。同理,当T[0]!=T[j]是可以排除next[j]=-1的情况。
当k==0时,若S[i]!=T[j]产生失配,此时next[j]只有0、-1两种情况,原理和上面相同,若T[0]==T[j],则next[j]=-1,否则next[j]=0
个人理解:
今天想了这么多,其实这个求next[j]的算法本质不是那么难了,主要是为了避免简单匹配的指针回溯并使模式串尽可能大距离得向右移动来与原串匹配。(避免回溯和最大移动是措施,避免重复无效匹配是目的,理解next[j]值求解的关键所在!)
其实在没学习计算机之前,我们之前在做同样的事情时,脑子里就是这种想法,比如原串S="adfgahhklm"和匹配串T="hkl",我们脑子里首先想得就是从原串里找出匹配串中第一个字符'h',然后依次向下匹配,并不会像简单匹配那么笨,还要回溯。
关于next[j]的作用,主要是使模式串尽可能大距离得向右移动来与原串匹配,这样做会避免无效多余的匹配,也就是去利用串T本身的性质(已经与S比较过得相同的部分)。比如原串S="adadaeh",、和匹配串T="adaeh",当执行到S[2]==T[2]时,依次向下匹配即马上判断S[3]与T[3](此时已经知道S和T中有相同的部分"ada"),发现失配后,直接比较S[3]与T[1],原因和理由很简单(不过也是精髓),为了将上一趟的T[0]与本趟的T[2]对齐(因为T[0]=T[2])。整个过程如果换成数学语言表述就是S[2]=T[2],T[0]=T[2],所以S[2]=T[0],就是使T[0]对齐T[2],从而只需直接比较S[3]与T[1],而不必考虑之前的(之前的已经比较过了)。再通俗一点就是,之前的比较已经“记住”前面的元素,利用前面的结果去比较下一个而不必重复比较。
这个例子的图解如下:
S a d a d a e h
T a d a e h T[3]!=S[3],产生失配
T a d a e h 比较S[3]与T[1],由于T本身的性质(之前已经比较过,知道与S相同的部分是"ada"),直接使T[0]与上一次的T[2]对齐后比较
举例:
求T=“abcac”的模式函数的值。
|
下标 |
0 |
1 |
2 |
3 |
4 |
|
T |
a |
b |
c |
a |
c |
|
next |
-1 |
0 |
0 |
-1 |
1 |
若T=“abcab”将是这样:
|
下标 |
0 |
1 |
2 |
3 |
4 |
|
T |
a |
b |
c |
a |
b |
|
next |
-1 |
0 |
0 |
-1 |
0 |
若T=“ababcaabc”将是这样:
|
下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
T |
a |
b |
a |
b |
c |
a |
a |
b |
c |
|
next |
-1 |
0 |
-1 |
0 |
2 |
-1 |
1 |
0 |
2 |
若T=“abCabCad”将是这样:
|
下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
T |
a |
b |
C |
a |
b |
C |
a |
d |
|
next |
-1 |
0 |
0 |
-1 |
0 |
0 |
-1 |
4 |
若T=“adCadCad”将是这样:
|
下标 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
T |
a |
d |
C |
a |
d |
C |
a |
d |
|
next |
-1 |
0 |
0 |
-1 |
0 |
0 |
-1 |
0 |
四. 求串T的模式值next[n]的函数
鄙人表示比较坑爹,不能理解这个函数的内涵,不是很懂最初是如何设计的,只能膜拜了
void get_next(SString T,int next[])
{
int i=0,j=-1,m=StrLength(T);
next[0]=-1;
while(i<m)
{
if(j==-1||T[i]==T[j])
{
++i;
++j;
if(T[i]!=T[j])
next[i]=j;
else
next[i]=next[j];
}
else
j=next[j];
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号