跟我一起学算法——分治法
@
分治法(Divide and Conquer)
1.定义
对于具备以下特点的问题:
- 原问题可以分解为若干个与原问题性质相类似的子问题
- 问题的规模缩小到一定程度后可方便求出解
- 子问题的解可以合并得到原问题的解
- 分解出的各个子问题应相互独立
当这类问题较复杂或规模较大时,将它分解为若干子问题,通过合并子问题的解得到原问题的解。
2.适用条件分析
分治法所能解决的问题一般具有以下几个特征:
- 该问题的规模缩小到一定的程度就可以容易地解决
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质
- 利用该问题分解出的子问题的解可以合并为该问题的解
- 问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题
上述的第一条特征绝大多数问题都可以满足,第二条是分治法应用的前提,反映了递归思想的应用,
第三条特征是关键,如果具备了第一条和第二条特征,而不具备第三条特征,则可以考虑贪心算法
或动态规划算法;第四条特征涉及到分治法的效率,如果各个子问题不是独立的,则分治法要重复
地解公共子问题,动态规划算法解决效率更高。动态规划法=分治算法思想+解决子问题冗余情况
3.步骤
- 分解
- 求解子问题
- 合并子问题的解
应用1:归并排序
步骤
- 把具有n个元素的数组分解为二个n/2大小的子数组
- 递归地分解子数组,直到子数组只包含一个元素为止
- 合并已排好序的子数组使之成为一个新的排好序的子数组,重复合并直到得到原问题的解
算法
算法分析
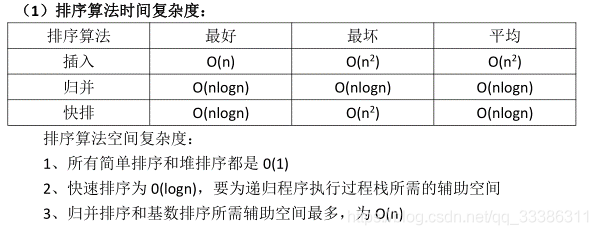
应用2:快速排序
基本思想
在当前的无序区A[p..r]中任取一个元素x作为比较的基准,并用该基准将当前无序区分为左右二个
较小的无序区A[p..q-1]和A[q+1..r],使得左边的无序区A[p..q-1]中的元素均小于基准元素x,
右边的无序区A[q+1..r]中的元素均大于x。
算法
quicksort(A,p,r)
if p<r
q=patition(A,p,r)
quicksort(A,p,q-1)
quicksort(A,q+1,r)
partition(A,p,r)
x=A[r]
i=p-1
for j=p to r-1
if A[j]≤x
i=i+1
exchange(A[i],A[j])
exchange(A[i+1],A[r])
return i+1
算法分析
partition算法时间为: θ(n) --> Quicksort的时间:T(n) = T(q)+T(n-q-1)+ θ(n)
最坏情况:二个无序区的大小分别为n-1和0,T(n) = θ(n^2)
最好情况:O(nlgn)
参考
《算法导论》



