基础算法改进——快速排序的改进
基础算法改进——快速排序的改进
简介:
快排三种实现方式:
- 挖坑法
- 左右指针法
- 前后指针法
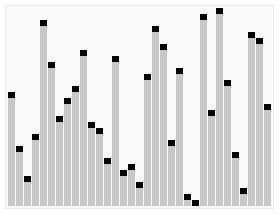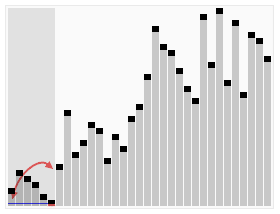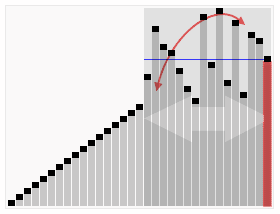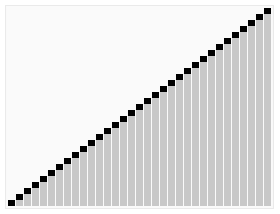

改进方法:
- 随机化: 数组打乱random_shuffle(a+1,a+n+1); //打乱它
- 小区间插入排序:减少对栈的访问
- 基准选择:
- 随机:但是随机数的生成本身是一种代价,根本减少不了算法其余部分的平均运行时间。
- 三值取中数:经验得知,选取左端,右端,中心元素的中值会减少快排大约 14%的比较。
- 中位数:选取中位数的可以在 O(n)时间内完成。(在平均情况下,任何顺序统计量(特别是中位数)都可以在线性时间内得到) - 三路快速排序算法:划分成三部分:小于、等于、大于
- 消除递归:利用栈
挖坑法实现快排,代码如下:
template<class T>//插入排序
void CC_InsertSort(T* begin, int Len)
{
T t, * A = begin;
int i, j;
for (i = 1; i <= Len; i++)
if (A[i] < A[i - 1]) {
t = A[i];
for (j = i - 1; j >= 0 && A[j] > t; j--)
A[j + 1] = A[j];
A[j + 1] = t;
}
}
template<class T>//挖坑快速排序
int partition(T* begin, int Len) {
T* A = begin;
int Tem = A[0];//选取比较的基准,其位置也就是初始的坑位
int i = 0, j = Len - 1;
while(i < j) {
while (A[j] >= Tem && i < j)
j--;
if(i < j)
A[i++] = A[j];
while (A[i] <= Tem && i < j)
i++;
if (i < j)
A[j--] = A[i];
}
A[j] = Tem;
return j;
}
template<class T>
void CC_QuickSort(T* A,int Len)
{
if (Len <= 1) return;
int k = partition(A, Len);
CC_QuickSort<int>(A, k);
CC_QuickSort<int>(&A[k+1], Len - k-1);
}
改进算法:
选取(a,b,c)(左端,右端,中心元素)三个数的中位数的方法:
- m = max(a,b); n = max(b,c);
- 如果m==n ,说明b是三者最大的,那么(a,c)中的最大值就是三者的中值
- 否则:如果m和n都不等于b,说明b是三者最小的那个,那么(a,c)中的较小者就是三者的中值
- 否则,(a,c)一个大于b一个小于b,说明b为中值。
template<class T>//插入排序
void CC_InsertSort(T* begin, int Len)
{
T t, * A = begin;
int i, j;
for (i = 1; i <= Len; i++)
if (A[i] < A[i - 1]) {
t = A[i];
for (j = i - 1; j >= 0 && A[j] > t; j--)
A[j + 1] = A[j];
A[j + 1] = t;
}
}
template<class T>//返回左端,右端,中心元素的中值的位置
int GetMid(T* begin, int Len) {
if (Len <= 1)
return 0;
int a = begin[0], b = begin[Len / 2], c = begin[Len-1];
int m = std::max(a, b), n = std::max(b, c);
if (m == n)
if (a > c)
return 0;
else
return Len-1;
else if (m != b && n!= b)
if (a > c)
return Len-1;
else
return 0;
else
return Len / 2;
}
template<class T>//挖坑快速排序
int partition(T* begin, int Len) {
T* A = begin;
int mid = GetMid<int>(begin, Len);//中位
std::swap(A[mid], A[0]);//把中位数换到第一位
int Tem = A[0];//选取比较的基准,其位置也就是初始的坑位
int i = 0, j = Len - 1;
while(i < j) {
while (A[j] >= Tem && i < j)
j--;
if(i < j)
A[i++] = A[j];
while (A[i] <= Tem && i < j)
i++;
if (i < j)
A[j--] = A[i];
}
A[j] = Tem;
return j;
}
template<class T>
void CC_QuickSort(T* A,int Len)
{
if (Len <= 1) return;
if (Len < 15) { //小区间采用插入排序
CC_InsertSort(A, Len-1);
return;
}
int k = partition(A, Len);
CC_QuickSort<int>(A, k);
CC_QuickSort<int>(&A[k+1], Len - k-1);
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号