数据结构实验--唯一的确定一棵二叉树

一、问题描述

如果给出了遍历二叉树的前序序列和中序序列，则可以构造出唯一的一棵二叉树。试编写实现上述功能的程序。

【基本要求】
已知一棵二叉树的前序和中序序列，试设计完成下列任务的一个算法：
（1）构造一棵二叉树；
（2）证明构造正确（即分别以前序和中序遍历该树，将得到的结果与给出的序列进行比较）。
（3）对该二叉树进行后序遍历，输出后序遍历序列。
（4）用凹入法输出该二叉树。

【测试数据】
（1）前序序列为ABDEGCFHIJ，中序序列为DBGEAHFIJC。
（2）前序序列为-+abc/de，中序序列为a+bc-d/e 。

【拓展内容】
由原表达式构造二叉树。测试数据(a+b) ×c-d/e

二、需求分析

需要设计有以下几个功能的程序：

• 1：由已知的前序和后续序列构建二叉树
• 2：分别用三种序列（前中后）输出二叉树
• 3：用凹入法输出二叉树

输入：分别输入前序序列和后序序列

输出：四种方法分别输出该二叉树

拓展功能：根据输入的中缀表达式(四则运算)，创建二叉树

三、设计

3.1 概要设计

（1）数据结构设计
根据题目要求易知本程序采用树结构作为基本结构，但在操作过程中也要用字符数组或者字符串类型储存计算过程中的表达式，考虑到需要多次使用截取部分字符串的

（2）算法设计
根据前序遍历的特点, 知前序序列(PreS)的首个元素(PreS[0])为二叉树的根(root), 然后在中序序列(InS)中查找此根(root), 根据中序遍历特点, 知在查找到的根(root) 前边的序列为根的左子树的中序遍历序列, 后边的序列为根的右子树的中序遍历序列。 设在中序遍历序列(InS)根前边有left个元素. 则在前序序列(PreS)中, 紧跟着根(root)的left个元素序列(即PreS[1…left]) 为根的左子树的前序遍历序列, 在后边的为根的右子树的前序遍历序列.而构造左子树问题其实跟构造整个二叉树问题一样，只是此时前序序列为PreS[1…left]), 中序序列为InS[0…left-1], 分别为原序列的子串, 构造右子树同样, 显然可以用递归方法解决。

建立完二叉树之后，很容易建立三个函数用递归的算法遍历输出已经建立的二叉树的前中后三种序列，对于凹入法，可以基于前序遍历输出，在输出的时候控制格式，即根据层高判断字符前面输出的空格数，在字符后输出与空格对应的点或其他字符，保持总的字符数不变。

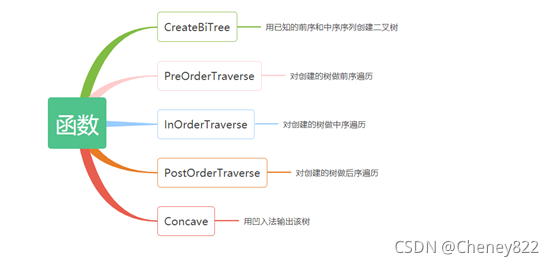
3.2 详细设计

1.类的设计

由于本算法基于树来实现，首先要设计树的节点类，包括数据域和指针域，指针域包括左子树和右子树。树类包括一个指向树的节点类的指针和其他若干函数

2. 遍历函数设计

void PreOrderTraverse(BiNode* t)
{
	if (t == NULL) return;	
		cout << t->Data;
		PreOrderTraverse(t->L_Child);
		PreOrderTraverse(t->R_Child);
}//前序遍历

遍历的算法如上，基于递归的思想，首先把t等于NULL作为递归出口
输出当前数据之后，依次递归访问左孩子和右孩子
对于中序和后续遍历仅需改变输出语句与访问左右孩子的顺序

3. 创建二叉树函数设计

void CreateBiTree(BiNode* t, string Pres, string Ins)//t为要建立的二叉树,pres和ins分别为前序和中序序列

{
	if (Pres.length() == 0) { t = NULL; return; }//递归出口：当前前序序列长度为零

	//前序序列的第一位Pres[0]即为根
	int Location = Ins.find(Pres[0]);//根在中序序列中的位置，以此位置把中序序列分开
	string L_In = Ins.substr(0, Location);//左孩子的中序序列
	string R_In = Ins.substr(Location + 1);//右孩子的中序序列
	int L_length = L_In.length();//左孩子的长度即左子树节点个数

	//在原前序序列中 按顺序 提取出子树节点个数个字符  当作对应子树新的前序序列
	string L_Pre = Pres.substr(1, L_length);//左孩子的前序序列
	string R_Pre = Pres.substr(1 + L_length);//右孩子的前序序列

	t->Data=Pres[0];//当前前序序列的首位赋给t的data

	if(L_Pre.length()){
	t->L_Child = new BiNode();
	CreateBiTree(t->L_Child, L_Pre, L_In);//递归创建左孩子
	}
	if(R_Pre.length()){
	t->R_Child = new BiNode();
	CreateBiTree(t->R_Child, R_Pre, R_In);//递归创建右孩子
	}
}

创建二叉树的算法如上，表示图如下：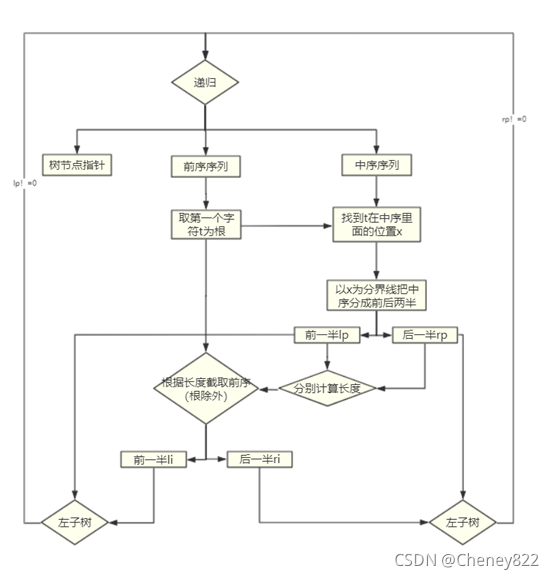

4.凹入法输出设计

void Concave(BiNode* p, string ss, string RR)
{
	if (p == NULL)   return; //递归出口

	ss += "   ";//用来控制格式，每次多输出三个空格
	RR = RR.substr(3);//用来控制格式,字符后输出特定的符号，并保证最后一位对齐
	cout << ss << p->Data << RR << endl;
	Concave(p->L_Child, ss,RR);
	Concave(p->R_Child, ss,RR);
}

凹入法打印二叉树的算法如上：主函数调用的语句如下
Concave(TreeRoot, “”, “…”);

四、测试数据及测试结果：

测试输入：前序序列为ab，中序序列为ab 。
测试目的：设计该输入的目的在于测试程序在哪方面可能存在漏洞；
实际输出：经检验该输出符合预期的要求

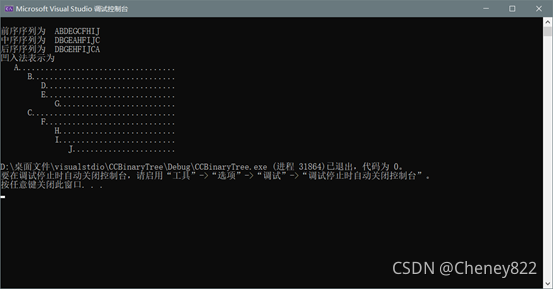
测试输入：前序序列为ABDEGCFHIJ，中序序列为DBGEAHFIJC。
测试目的：设计该输入的目的在于测试程序在哪方面可能存在漏洞；
实际输出：经检验该输出符合预期的要求

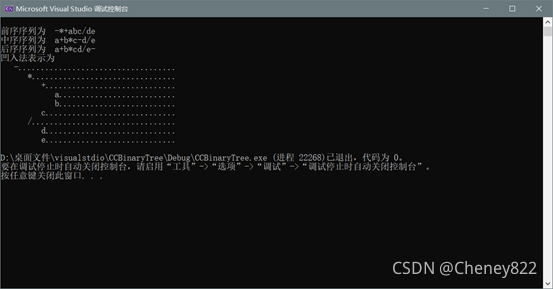
测试输入：前序序列为-+abc/de，中序序列为a+bc-d/e 。
测试目的：设计该输入的目的在于测试程序在哪方面可能存在漏洞；
实际输出：经检验该输出符合预期的要求