CSP-S模拟19

A. 木棍

发现一共就

$(334)(3322)(442)(4222)(22222)$

几种情况，发现 $2$ 通配，最后考虑他即可，先考虑 $334$

然后 $3 /4 $ 必然只剩一种可以贡献，分别算一下，最后处理剩下的 $2$ 即可

code

#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<map>
#include<set>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;

ll read(){
	ll x = 0; char c = getchar();
	while(!isdigit(c))c = getchar();
	do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
	return x;
}
ll t, a, b, c;
void solve(){
	a = read(), b = read(), c = read();
	ll ans = 0;
	ll n334 = min(b / 2, c);
	ans += n334;
	b -= 2 * n334; c -= n334;
	if(b > 1){
		ll n3322 = min(a / 2, b / 2);
		ans += n3322;
		a -= n3322 * 2;
	}
	if(c > 0){
		ll n442 = min(c / 2, a);
		ans += n442;
		c -= n442 * 2; a -= n442;
		if(c > 0){
			ll n4222 = min(c, a / 3);
			ans += n4222;
			a -= n4222 * 3;
		}
	}
	if(a > 0){
		ans += a / 5;
	}
	printf("%lld\n",ans);
}
int main(){
	t = read();
	for(int ask = 1; ask <= t; ++ask)solve();
	return 0;
}

B. 环

按照 $a_i$ 排序，显然不影响答案，而且多了一个美妙性质，前面能选后面一定能选

考虑为了不重复统计答案，我们在每个环出现在左侧的最大的点处统计答案

于是我们就需要知道对于左侧的每个点 $i$ ，用前 $i - 1$ 个左侧点， $a_i$ 个右侧点能够拼成多少链

我们依然按照左侧点顺序考虑令 $f_{i, j}$ 表示考虑左侧前 $i$ 个点，右侧前 $a_i$ 个点，散点和链的个数为 $j$ 的方案数

利用左侧点对其进行拼接

该状态将在考虑了之后某些左侧点，进行若干次拼接，令 $j$ 个散点和链拼成一条链时对答案产生贡献

考虑由 $f_{i - 1} - > f_i$ 先不考虑 $i$ 进行拼接的贡献

$f_{i,j}$ 的 $j$ 可以是之前的若干散点或链，也可以是 $a_i - a_{i - 1}$ 个新增右部点，于是考虑选择了多少新增点，和之前的部分进行组合，你可以用组合数来搞

~~发现他比较像一个背包的形式，就是容量价值都为 $1$ 的物品，于是直接循环可以去掉组合数~~

于是你有了左侧前 $i - 1$ 个点，右侧前 $a_i$ 个点，散点和链的个数为 $j$ 的方案数

那么取 $f_{i, 1}$ 减去散点的方案，即 $a_i$ 即为 $i$ 对答案的贡献

现在考虑 $i$ 对后续点的贡献，那么用 $i$ 去拼接两个散点或链，但是发现链有两端，选择散点和链的方案数不同

于是给他们强制定向进行拼接，于是 $f_{i,j} += f_{i,j + 1}*(j+1)*j$

思考这样的话，每个环会被顺时针和逆时针统计一次，于是最后答案乘上$inv2$

code

#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<map>
#include<set>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;

int read(){
	int x = 0; char c = getchar();
	while(!isdigit(c))c = getchar();
	do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
	return x;
}
const int maxn = 5005;
const int mod = 998244353;
const int inv2 = 499122177;
int n, a[maxn], f[maxn];
void add(int &x, int y){x += y; x = x >= mod ? x - mod : x;}
int main(){
	n = read();
	for(int i = 1; i <= n; ++i)a[i] = read();
	sort(a + 1, a + n + 1);
	int ans = 0; f[0] = 1;
	for(int i = 1; i <= n; ++i){
		for(int j = a[i - 1] + 1; j <= a[i]; ++j)
			for(int k = j; k >= 1; --k)
				add(f[k], f[k - 1]);
		add(ans, (f[1] - a[i] + mod) % mod);
		for(int j = 0; j <= a[i]; ++j)add(f[j], 1ll * f[j + 1] * (j + 1) % mod * j % mod);
	}
	ans = 1ll * ans * inv2 % mod;
	printf("%d\n",ans);
	return 0;
}

C. 传令

寒假考过将军令，跟这题挺像的

二分答案 $k$ ，按照点的深度顺序处理，每次选择最深的没有选过的点的 $k$ 级祖先，然后去标记删点

复杂度显然是假的，但是记录一下之前扩展的范围就能莽过去，而且我不会如何构造数据卡

code

#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<map>
#include<set>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;

int read(){
	int x = 0; char c = getchar();
	while(!isdigit(c))c = getchar();
	do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
	return x;
}
const int maxn = 200055;
int n, k;
int head[maxn], tot;
struct edge{int to, net;}e[maxn << 1 | 1];
void add(int u, int v){
	e[++tot].net = head[u];
	head[u] = tot;
	e[tot].to = v;
}
int dep[maxn], fa[maxn][19];
void dfs(int x){
	for(int i = head[x]; i; i = e[i].net){
		int v = e[i].to;
		if(v == fa[x][0])continue;
		fa[v][0] = x; dep[v] = dep[x] + 1;
		dfs(v);
	}
}
int d[maxn];
bool cmp(int x, int y){return dep[x] > dep[y];}
int del[maxn];

int get_fa(int x, int k){
	for(int i = 0; i <= 18; ++i)if((1 << i) & k){
		x = fa[x][i];
	}
	return x;
}
void kill(int x, int fa, int dis){
	del[x] = dis + 1;
	if(dis == 0)return;
	for(int i = head[x]; i; i = e[i].net){
		int v = e[i].to;
		if(v == fa)continue;
		if(del[v] < dis)kill(v, x, dis - 1);
	}
}

bool check(int mid){
	for(int i = 1; i <= n; ++i)del[i] = 0;
	int cnt = 0;
	for(int i = 1; i <= n; ++i)if(!del[d[i]]){
		int x = get_fa(d[i], mid);
		kill(x, 0, mid); ++cnt; if(cnt > k)return false;
	}
	return true;
}
int main(){
	n = read(), k = read();
	for(int i = 1; i < n; ++i){
		int u = read(), v = read();
		add(u, v); add(v, u);
	}
	fa[1][0] = 1;
	dfs(1);
	for(int j = 1; j <= 18; ++j)
		for(int i = 1; i <= n; ++i)
			fa[i][j] = fa[fa[i][j - 1]][j - 1];
	for(int i = 1; i <= n; ++i)d[i] = i;
	sort(d + 1, d + n + 1, cmp);
	int l = 0, r = n, ans = n;
	while(l <= r){
		int mid = (l + r) >> 1;
		if(check(mid))r = mid - 1, ans = mid;
		else l = mid + 1;
	}
	printf("%d\n",ans);
	return 0;
}

D. 序列

先不考虑彩色序列的限制，$a$ 出现的次数为 $k^{n - m}(n - m + 1)$

即钦定 $a$ 开始位置，前后随便选

然后减去不合法的方案，分三种情况

$a$ 本身就含有彩色序列，那么一定合法
没有，并且 $a$ 没有重复元素

我们需要计算出长度为 $n$ 的由 $1-k$ 组成的非彩色序列中 $a$ 的出现次数

限制有点多，改成统计长度为 $n$ 的由 $1-k$ 组成的非彩色序列中长度为$m$ 的没有重复色彩的子段的出现次数

他们方案数是相同的，有 $A_{k}^{m}$种，所以算出答案除以 $k^{\underline m}$

设 $f_{i, j}$表示长度为 $i$ 的非彩色序列，最后极长颜色不同后缀长度为 $j$ 的方案数

转移

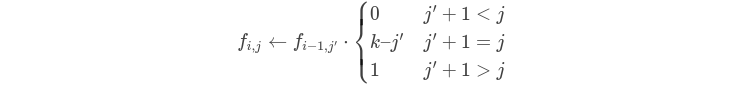
注意大于等于$k$ 的就不是我们需要的了

(图片来自 $luogu$)

显然可以后缀和优化

初值 $f_{0,0} = 1$

令 $g_{i, j}$与之定义类似，只是他为长度为$m$ 的没有重复色彩的子段的出现次数，转移与 $f$ 相同

初值为 $g_{i,j} += f_{i,j}[j >= m]$

最后取 $\sum g_n$ 作为答案

没有，并且 $a$ 有重复元素

找到 $a$ 的极长重复色彩的前后缀，长度记为$l, r$

于是可以令 $f_{0,0} .... f_{0,l} = 1$ 进行上面的转移，转移得到合法的前缀（倒着，但是不影响）

$g_{0,0} ....g_{0,r} = 1$同理，（与2里的$g$不同，是合法的后缀）

最后去枚举 $a$ 的开头位置，前后合法方案拼接起来即可

再搬一个 $luogu$的图

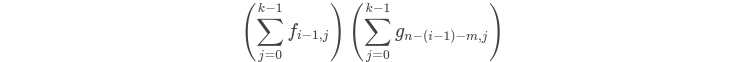
参考了洛谷题解

code

#include<cstring>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<map>
#include<set>
#include<bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef unsigned long long ull;


int read(){
	int x = 0; char c = getchar();
	while(!isdigit(c))c = getchar();
	do{x = x * 10 + (c ^ 48); c = getchar();}while(isdigit(c));
	return x;
}
const int maxn = 25005;
const int mod = 1e9 + 7;
int qpow(int x, int y){
	int ans = 1;
	for(; y; y >>= 1, x = 1ll * x * x % mod)if(y & 1) ans = 1ll * ans * x % mod;
	return ans;
}
int n, k, m, a[maxn], ans, f[maxn][405], g[maxn][405];
bool vis[maxn];
int l, r;
void calc(int f[][405]){
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j < k; ++j)f[i][j] = (f[i - 1][j] + 1ll * (f[i - 1][j - 1] - f[i - 1][j] + mod) % mod * (k - j + 1) % mod ) % mod;
		for(int j = k - 1; j >= 0; --j)f[i][j] = (f[i][j] + f[i][j + 1]) % mod;
	}
}
void solveunique(){
	f[0][0] = 1;
	for(int i = 1; i <= n; ++i){
		for(int j = 1; j < k; ++j){
			f[i][j] = (f[i - 1][j] + 1ll * (f[i - 1][j - 1] - f[i - 1][j] + mod) % mod * (k - j + 1) % mod ) % mod;
			g[i][j] = (g[i - 1][j] + 1ll * (g[i - 1][j - 1] - g[i - 1][j] + mod) % mod * (k - j + 1) % mod ) % mod;
			if(j >= m)g[i][j] = (g[i][j] + f[i][j]) % mod;
		}
		for(int j = k - 1; j >= 0; --j)f[i][j] = (f[i][j] + f[i][j + 1]) % mod;
		for(int j = k - 1; j >= 0; --j)g[i][j] = (g[i][j] + g[i][j + 1]) % mod;
	}
	int nans = g[n][0];
	for(int i = k; i > k - m; --i)nans = 1ll * nans * qpow(i, mod - 2) % mod;
	ans = (ans - nans + mod) % mod;
}
bool checkcolor(){
	for(int i = 1, j = k; j <= m; ++j, ++i){
		for(int p = 1; p <= k; ++p)vis[p] = false;
		for(int p = i; p <= j; ++p)if(vis[a[p]])goto nxt;else vis[a[p]] = true;
		return true; nxt:;
	}
	return false;
}
void solvemulti(){
	for(int i = 0; i <= l; ++i)f[0][i] = 1;
	for(int i = 0; i <= r; ++i)g[0][i] = 1;
	calc(f); calc(g);
	int nans = 0;
	for(int i = 0; i <= n - m; ++i)nans = (nans + 1ll * f[i][0] * g[n - m - i][0] % mod) % mod;
	ans = (ans - nans + mod) % mod;
}
int main(){
	n = read(), k = read(), m = read();
	for(int i = 1; i <= m; ++i)a[i] = read();
	ans = 1ll * qpow(k, n - m) * (n - m + 1) % mod;
	if(checkcolor())goto P;
	l = 0; r = m + 1;
	for(int i = 1; i <= k; ++i)vis[i] = false;
	for(int i = 1; i <= m; ++i){
		if(vis[a[i]]){l = i - 1; break;}
		else vis[a[i]] = true;
	}
	for(int i = 1; i <= k; ++i)vis[i] = false;
	for(int i = m; i >= 1; --i){
		if(vis[a[i]]){r = m - i; break;}
		else vis[a[i]] = true;
	}
	if(l == 0 && r == m + 1)solveunique();
	else solvemulti();
	P:;
	printf("%d\n",ans);
	return 0;
}

posted @ 2022-10-16 17:35 Chen_jr 阅读(41) 评论(0) 编辑收藏举报

刷新页面返回顶部

Chen_jr

CSP-S模拟19

A. 木棍

B. 环

C. 传令

D. 序列

公告