2022NOIPA层联测5
A.挑战
签到题，从左往右推一遍即可， \(f_{i,j }\) 表示前面全部推到 \((i, j)\)的最小步数
code
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<set>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 400005;
int n;
char c[2][maxn];
int f[2][maxn], sum[maxn];
void solve(){
scanf("%d",&n);
scanf("%s%s",c[0] + 1, c[1] + 1);
for(int i = 1; i <= n; ++i)sum[i] = sum[i - 1] + (c[0][i] == '*') + (c[1][i] == '*');
int i;
f[0][0] = f[1][0] = f[0][1] = f[1][1] = 0;
for(i = 1; i <= n; ++i){
if(sum[i] == 0)continue;
if(sum[i - 1]){
f[0][i] = min(f[0][i - 1] + 1 + (c[1][i] == '*'), f[1][i - 1] + 2);
f[1][i] = min(f[1][i - 1] + 1 + (c[0][i] == '*'), f[0][i - 1] + 2);
}else{
f[0][i] = c[1][i] == '*';
f[1][i] = c[0][i] == '*';
}
if(sum[i] == sum[n])break;
}
printf("%d\n",min(f[0][i], f[1][i]));
}
int main(){
int t; scanf("%d",&t);
for(int ask = 1; ask <= t; ++ask)solve();
return 0;
}
B.天☆堂
发现会选择一段后缀，于是用后缀数组跑一下
然后 \(N^2\) \(LIS\) 每次取一个后缀，增加的贡献是长度减去 \(LCP\)
code
// #pragma GCC optimize(3)
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 10005;
int n;
int sa[maxn], rk[maxn], ht[maxn], cnt[maxn + maxn], ork[maxn + maxn], px[maxn + maxn], id[maxn];
bool cmp(int x, int y, int w){return ork[x] == ork[y] && ork[x + w] == ork[y + w];}
char c[maxn];
ll ans[maxn];
struct SA{
int n, m;
void clear(){
memset(rk, 0, sizeof(rk));
memset(sa, 0, sizeof(sa));
memset(ht, 0, sizeof(ht));
memset(cnt, 0, sizeof(cnt));
memset(ans, 0, sizeof(ans));
memset(ork, 0, sizeof(ork));
memset(id, 0, sizeof(id));
memset(px, 0, sizeof(px));
memset(st, 0, sizeof(st));
}
void built(){
m = max(n, 300);
for(int i = 1; i <= n; ++i)++cnt[rk[i] = c[i]];
for(int i = 1; i <= m; ++i)cnt[i] += cnt[i - 1];
for(int i = n; i >= 1; --i)sa[cnt[rk[i]]--] = i;
for(int w = 1; w <= n; w <<= 1){
int p = 0;
for(int i = n; i > n - w; --i)id[++p] = i;
for(int i = 1; i <= n; ++i)if(sa[i] > w)id[++p] = sa[i] - w;
for(int i = 1; i <= m; ++i)cnt[i] = 0;
for(int i = 1; i <= n; ++i)++cnt[px[i] = rk[id[i]]];
for(int i = 1; i <= m; ++i)cnt[i] += cnt[i - 1];
for(int i = n; i >= 1; --i)sa[cnt[px[i]]--] = id[i];
p = 0;
for(int i = 1; i <= n; ++i)ork[i] = rk[i];
for(int i = 1; i <= n; ++i)
if(cmp(sa[i], sa[i - 1], w))rk[sa[i]] = p;
else rk[sa[i]] = ++p;
if(p == n)break;
m = p;
}
}
void get_ht(){
int k = 0;
for(int i = 1; i <= n; ++i){
if(k) --k;
while(c[i + k] == c[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int st[maxn][19];
int lg[maxn];
void get_st(){
for(int i = 2; i <= n; ++i)lg[i] = lg[i >> 1] + 1;
for(int i = 1; i <= n; ++i)st[i][0] = ht[i];
for(int j = 1; (1 << j) <= n; ++j)
for(int i = 1; i + (1 << j) - 1 <= n; ++i)
st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
}
int get_lcp(int x, int y){
if(x == y)return n - x + 1;
x = rk[x], y = rk[y];
if(x > y)swap(x, y);
++x;
int k = lg[y - x + 1];
return min(st[x][k], st[y - (1 << k) + 1][k]);
}
void solve(){
for(int i = 1; i <= n; ++i){
int s = n - sa[i] + 1;
ans[i] = s;
for(int j = 1; j < i; ++j)if(sa[j] < sa[i])
ans[i] = max(ans[i], ans[j] + s - get_lcp(sa[i], sa[j]));
}
ll pt = 0;
for(int i = 1; i <= n; ++i)pt = max(pt, ans[i]);
printf("%lld\n",pt);
}
void init(){
scanf("%d",&n);
scanf("%s",c + 1);
n = strlen(c + 1);
built(); get_ht(); get_st();
solve(); clear();
}
}S;
int main(){
int t; scanf("%d",&t);
for(int ask = 1; ask <= t; ++ask)S.init();
return 0;
}
C.药丸
卡特兰数搞一下
\(\sum_{i = 0}^{n}C_{n}^{i}\sum_{j = l,2|(i + j)}^{r}(C_{i}^{(i+j)/ 2} -C_{i}^{(i+j + 2)/ 2} )\)
解释一下，关于卡特兰可以想到坐标系以及跨越的那条线，于是枚举
最终加血 \(j\)， 一共操作 \(i\)， 那么加血\((i + j) / 2\)次, 扣血 \((i - j) / 2\)次，相当于走到 \(((i + j) / 2, (i - j) / 2)\) 如果过 \(y = x + 1\)那么会到对称点，所以是后面两个组合数相减的形式
令 \(jl = (i + l + 1) / 2, jr = (i + r) / 2\)
把后面的\(\sum\)展开，两两消去只剩下 \(\sum_{i = 0}^{n}C_{n}^{i} (C_{i}^{jl} - C_{i}^{jr +1})\)
然后考虑处理模数不是质数的问题
把模数质因数分解为 \(p_1^{c1}p_2^{c2}..\)
然后把所有数写成 \(x \times p1^{k1}p2^{k2}...\)
重新定义一下乘法除法，用的时候转成数字即可
那边题解讲的很好。
code
#include<cstdio>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 100005;
int n, mod, l, r;
int prime[25], cpr[25], cnt;
ll phi;
int qpow(int x, int y){
int ans = 1;
for(; y; y >>= 1, x = 1ll * x * x % mod) if(y & 1)ans = 1ll * ans * x % mod;
return ans;
}
struct num{
int x, inv, p[25];
num(){x = inv = 1; for(int i = 1; i <= cnt; ++i)p[i] = 0;}
void ch(int y){
for(int i = 1; i <= cnt; ++i){
while(y % prime[i] == 0){y /= prime[i], ++p[i];}
}
y %= mod; x = y; inv = qpow(y, phi - 1);
}
int print(){
int ans = x;
for(int i = 1; i <= cnt; ++i){
ans = 1ll * ans * qpow(prime[i], p[i]) % mod;
}
return ans;
}
friend num operator * (const num &x, const num &y){
num ans;
ans.x = 1ll * x.x * y.x % mod; ans.inv = qpow(ans.x, phi - 1);
for(int i = 1; i <= cnt; ++i)ans.p[i] = x.p[i] + y.p[i];
return ans;
}
friend num operator / (const num &x, const num &y){
num ans;
ans.x = 1ll * x.x * y.inv % mod; ans.inv = qpow(ans.x, phi - 1);
for(int i = 1; i <= cnt; ++i)ans.p[i] = x.p[i] - y.p[i];
return ans;
}
}fac[maxn], nu[maxn];
void init(int mx){
phi = mx;
for(int i = 2; i * i <= mx; ++i){
if(mx % i)continue;
prime[++cnt] = i;
phi = 1ll * phi / i * (i - 1);
while(mx % i == 0)mx /= i, ++cpr[cnt];
}
if(mx > 1){
prime[++cnt] = mx;
++cpr[cnt];
phi = phi / mx * (mx - 1);
}
}
int c(int n, int m){
if(n < 0 || m < 0 || n < m)return 0;
return ((fac[n] / fac[n - m]) / fac[m]).print();
}
int main(){
scanf("%d%d%d%d",&n,&mod,&l,&r);
init(mod);
fac[0].ch(1);
for(int i = 1; i <= n; ++i)nu[i].ch(i);
for(int i = 1; i <= n; ++i)fac[i] = fac[i - 1] * nu[i];
int ans = 0;
for(int i = 0; i <= n; ++i){
int jl = (i + l + 1) / 2, jr = (i + r) / 2 + 1;
ans = (ans + 1ll * c(n, i) * ((1ll * c(i, jl) - c(i, jr) + mod) % mod) % mod) % mod;
}
printf("%d\n",ans);
return 0;
}
D.按钮
考了费用流，比较离谱
建图
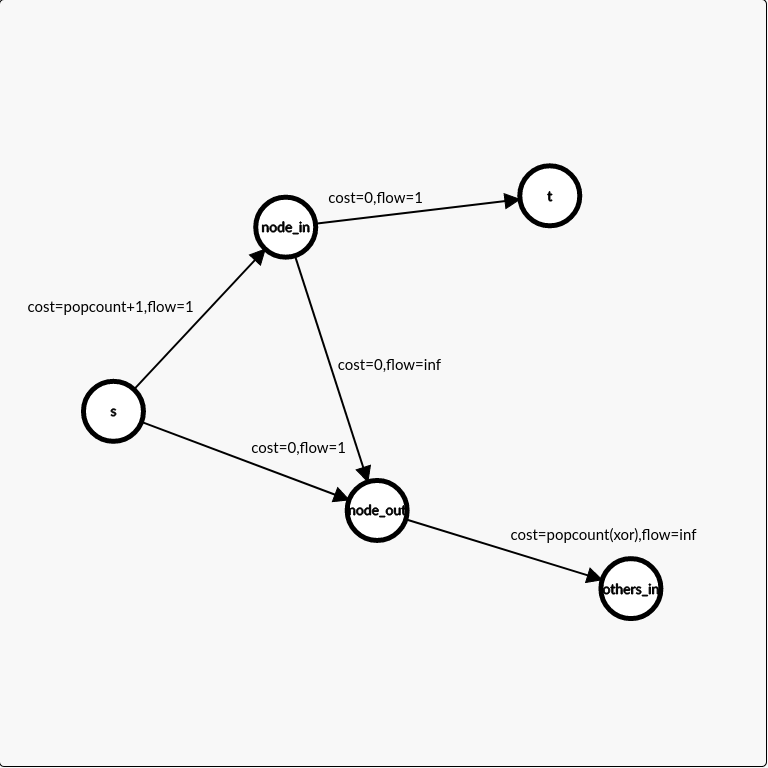
code
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<set>
#include<vector>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 500025;
const int inf = 0x3f3f3f3f;
int d, n, opt[maxn], cnt[maxn];
char c[15];
bool cmp(int x, int y){return cnt[x] > cnt[y];}
struct graph{
struct edge{
int to, net, val;
}e[maxn];
int head[maxn], tot;
void add(int u, int v, int w){
e[++tot].net = head[u];
head[u] = tot;
e[tot].to = v;
e[tot].val = w;
}
vector<int> v;
bool dfs(int x, int las){
for(int i = 0; i < d; ++i)if(opt[x] & (1 << i)){
if(las & (1 << i))continue;
v.push_back(i);
}
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(e[i].val > 0){
--e[i].val;
dfs(v, opt[x]);
return true;
}
if(e[i].val == 0)head[x] = e[i].net;
}
return false;
}
void print(){
for(int x : v)printf("%d ",x);
v.clear();
}
void gz(){
dfs(n + 1, 0); print();
while(dfs(n + 1, 0)){
printf("R ");
print();
}
}
}G;
struct MCMF{
struct edge{
int net, to, val, cost;
}e[maxn];
int head[maxn], tot = 1, s, t, mx, mi;
void add(int u, int v, int w, int c){
e[++tot].net = head[u];
head[u] = tot;
e[tot].to = v;
e[tot].val = w;
e[tot].cost = c;
}
void link(int u, int v, int w, int c){
add(u, v, w, c); add(v, u, 0, -c);
}
int dis[maxn];
bool vis[maxn];
bool spfa(){
memset(vis, 0, sizeof(vis));
memset(dis, 0x3f, sizeof(dis));
queue<int>q; q.push(s); dis[s] = 0;
while(!q.empty()){
int x = q.front(); q.pop(); vis[x] = 0;
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(e[i].val > 0 && dis[v] > dis[x] + e[i].cost){
dis[v] = dis[x] + e[i].cost;
if(!vis[v])q.push(v), vis[v] = 1;
}
}
}
return dis[t] != dis[maxn - 1];
}
int dfs(int x, int from){
if(from <= 0 || x == t)return from;
int res = from; vis[x] = 1;
for(int i = head[x]; i; i = e[i].net){
int v = e[i].to;
if(!vis[v] && e[i].val > 0 && dis[v] == dis[x] + e[i].cost){
int k = dfs(v, min(res, e[i].val));
res -= k;
e[i].val -= k;
e[i ^ 1].val += k;
if(res <= 0)break;
}
}
return from - res;
}
int mcmf(){
while(spfa()){
int k = dfs(s, inf);
mx += k;
mi += k * dis[t];
}
for(int i = 3; i <= tot; i += 2){
int u = e[i].to, v = e[i xor 1].to, w = e[i].val;
if((u == s && v > n) || w < 1 || v == t)continue;
if(u > n) u -= n; if(v > n) v -= n;
G.add(u, v, w);
}
return mi;
}
void init(){
s = n + n + 1, t = s + 1;
for(int i = 1; i <= n; ++i)link(s, i, 1, cnt[opt[i]] + 1);
for(int i = 1; i <= n; ++i)link(i, i + n, inf, 0);
for(int i = 1; i <= n; ++i)link(i, t, 1, 0);
for(int i = 1; i <= n; ++i)link(s, i + n, 1, 0);
for(int i = 1; i <= n; ++i){
for(int j = 1; j < i; ++j){
if((opt[j] & opt[i]) == opt[i]){
link(i + n, j, inf, cnt[opt[j] xor opt[i]]);
}
}
}
}
}W;
int main(){
scanf("%d%d",&d,&n);
for(int i = 1; i <= n; ++i){
scanf("%s",c);
for(int j = 0; j < d; ++j)opt[i] |= (c[j] - '0') << j;
}
int mx = 1 << d;
for(int i = 1; i < mx; ++i)cnt[i] = cnt[i - (i & -i)] + 1;
sort(opt + 1, opt + n + 1, cmp);
W.init();
int ans = W.mcmf() - 1;
printf("%d\n",ans);
G.gz();
return 0;
}
