CSP-S模拟5 D. o
由于某些原因单开一个
同步到洛谷题解
如果把每个数向前面第一个比他大的数连边，那么构成一个树形结构
可以发现对于一个 \(x\) 一直到下一个大于等于他的数之前的区间都会被他所影响，即都是他的子树，那么也就是说每个结点的子树是一个连续区间
因为是连续区间，所以他们被改变的时间也是连续的，我们考虑维护随时间变化的增量
在这个树形结构中他的父亲比他的父亲的父亲先影响到他，所以我们维护儿子与父亲的增量即可
其实上面这些废话只是告诉我们可以对每个位置得到一个四元组 \((t_0, l, r, d)\)
表示在 \([l,r]\) 区间, 从 \(t_0\) 时刻开始， 按照从左到右的位置顺序每个时刻都会在对应位置多 \(d\) 的贡献
我们把询问拆成查询两个前缀相减的形式 \(ans_r - ans_{l - 1}\) ，然后按照对时间进行扫描线，这样每个四元组的贡献大概就是下面这样
图有点丑，将就看吧
发现可以写成两个直角三角形差分的形式，如下下图
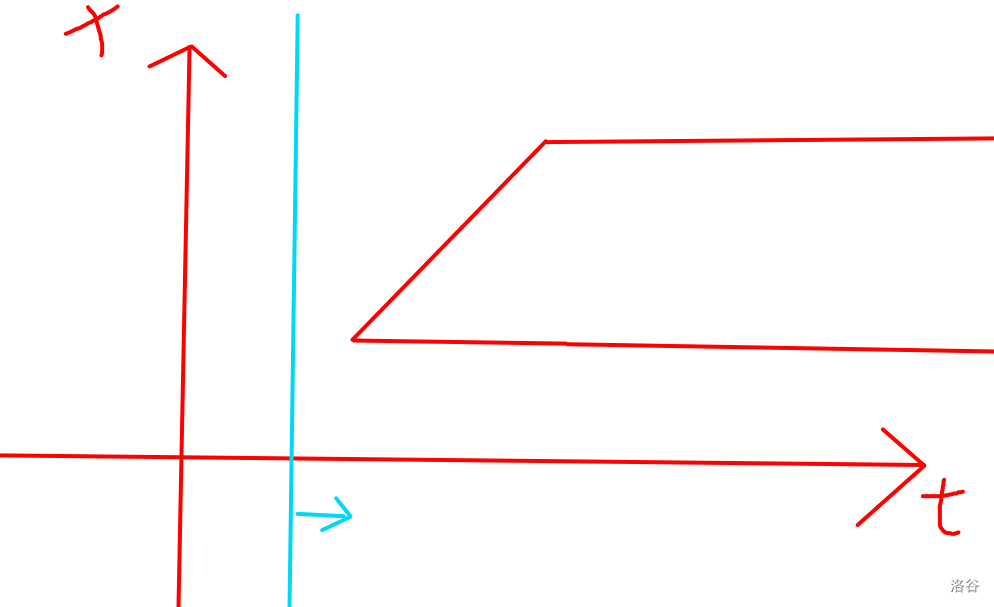
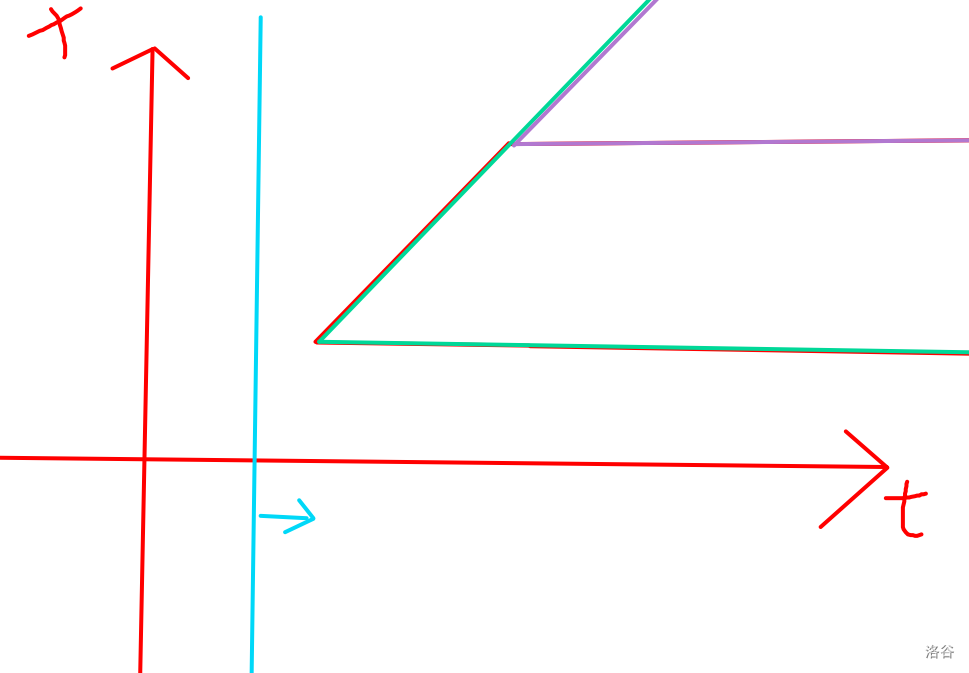
绿色减去紫色
所以四元组变成了两个三元组，就能够处理了
三元组 \((t_0, l, d)\) 表示 \(l\) 位置从 \(t_0\) 时刻开始每时刻向后面有 \(d\) 的增量
考虑对一个前缀 \(p\) 进行 \(t\) 时刻的询问， 他的贡献可以写成 \((min(p, l + t - t_0) - min(p, l - 1)) \times d\)
这样对于 \(p < l\) 我们也不需要特殊处理，因为一减就变成 \(0\) 了
也就是 \((t + min(p - t, l - t_0) - min(p, l - 1)) \times d\)
那么我们开四棵线段树分别维护
-
在 \(l\) 位置维护 \(l \times d\)
-
在 \(l - t_0\) 位置维护 \((l - t_0) \times d\)
-
在 \(l\) 位置维护 \(d\)
-
在 \(l - t_0\) 位置维护 \(d\)
询问对 \(min\) 取的是哪个值分开讨论即可
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 200005;
inline int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = (x << 3) + (x << 1) + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
int n, q, a[maxn];
int sta[maxn], fa[maxn], r[maxn];
struct que{
int p, t, id, opt;
friend bool operator < (const que &x, const que &y){
return x.t < y.t;
}
}ask[maxn + maxn];
struct opt{
int t0, l, d;
friend bool operator < (const opt &x, const opt &y){
return x.t0 < y.t0;
}
}o[maxn + maxn];
ll ans[maxn];
struct tree{
struct node{ll val, tag;}t[maxn << 3 | 1];
void push_up(int x){
t[x].val = t[x << 1].val + t[x << 1 | 1].val;
}
void modify(int x, int l, int r, int pos, ll val){
if(l == r){
t[x].val += val;
return;
}
int mid = (l + r) >> 1;
if(pos <= mid)modify(x << 1, l, mid, pos, val);
else modify(x << 1 | 1, mid + 1, r, pos, val);
push_up(x);
}
ll query(int x, int l, int r, int L, int R){
if(L <= l && r <= R)return t[x].val;
int mid = (l + r) >> 1; ll ans = 0;
if(L <= mid)ans += query(x << 1, l, mid, L, R);
if(R > mid)ans += query(x << 1 | 1, mid + 1, r, L, R);
return ans;
}
}t[4];
ll sum[maxn];
int main(){
n = read(), q = read();
for(int i = 1; i <= n; ++i)a[i] = read();
for(int i = 1; i <= n; ++i)sum[i] = sum[i - 1] + a[i];
for(int i = 1; i <= q; ++i){
int t = read(), l = read(), r = read();
ask[i + i - 1].id = ask[i + i].id = i;
ask[i + i - 1].t = ask[i + i].t = t;
ask[i + i - 1].p = l - 1, ask[i + i - 1].opt = -1;
ask[i + i].p = r, ask[i + i].opt = 1;
}
int top = 0;
for(int i = 1; i <= n; ++i){
while(top && a[sta[top]] < a[i])r[sta[top]] = i, --top;
fa[i] = sta[top]; sta[++top] = i;
}
while(top)r[sta[top--]] = n + 1;
sort(ask + 1, ask + q + q + 1);
int cnt = 0;
for(int i = 1; i <= n; ++i)if(fa[i]){
o[++cnt].d = a[fa[i]] - a[i];
o[cnt].l = i; o[cnt].t0 = i - fa[i];
if(r[i]){
o[++cnt].d = a[i] - a[fa[i]];
o[cnt].l = r[i]; o[cnt].t0 = r[i] - fa[i];
}
}
sort(o + 1, o + cnt + 1);
int op = 1;
for(int i = 1; i <= q + q; ++i){
while(op <= cnt && o[op].t0 <= ask[i].t){
t[0].modify(1, 0, n, o[op].l - 1, 1ll * (o[op].l - 1) * o[op].d);
t[1].modify(1, 0, n + n, o[op].l - o[op].t0 + n, 1ll * (o[op].l - o[op].t0) * o[op].d);
t[2].modify(1, 0, n, o[op].l - 1, o[op].d);
t[3].modify(1, 0, n + n, o[op].l - o[op].t0 + n, o[op].d);
++op;
}
ll nans = 0;
if(ask[i].p == 0)nans = 0;
else{
nans = ask[i].t * t[2].query(1, 0, n, 1, n);
nans = nans + t[1].query(1, 0, n + n, 1, ask[i].p - ask[i].t + n);
nans = nans + t[3].query(1, 0, n + n, ask[i].p - ask[i].t + n + 1, n + n) * (0ll + ask[i].p - ask[i].t);
nans = nans - t[0].query(1, 0, n, 1, ask[i].p);
nans = nans - t[2].query(1, 0, n, ask[i].p + 1, n) * 1ll * ask[i].p;
nans = nans + sum[ask[i].p];
}
ans[ask[i].id] += nans * ask[i].opt;
}
for(int i = 1; i <= q; ++i)printf("%lld\n", ans[i]);
return 0;
}
