CSP-S模拟4
A. 石子游戏
考场记得 \(NIM\) 游戏好像是把什么异或起来，然后瞎推半小时推出 \(\%(i + 1)\)
然后，从始至终都是这个暴力分。。。。。
关于正解，其实是优化了取模和异或的过程
设 \(cnt_x\) 表示 \(x\) 的出现次数，你会发现这里已经把问题转移到了值域上
设 \(f_{i, j}\) 表示 \(x - i\) 后 \(2^j\) 为 \(1\) 的数的个数
我们把数字拆成若干二进制位， 对每一位的贡献分开处理， 因为异或不进位，所以这是完全可行的
转移考虑分两部分处理，一部分是 \(f_{i + 2^{j + 1}, j}\) ， 因为 \(+2^{j + 1}\) 不会影响后面，这一部分是之前有的， 本次新加入的就是 \(\sum_{k = i + 2^j}^{i + 2 ^{j + 1} - 1}cnt_i\)
我们枚举当前的 \(m = i\), 要对 \(m + 1\) 取模，其实是对于每个 \(x\) 写成 \(x - k (m + 1)\) 的形式， 考虑枚举 \(k\) 每次处理 \([k(m + 1), (k + 1)(m + 1) - 1]\) ，记为区间 \([l, r]\)
我们要找的就是该区间内减去 \(l\) 后该位为 \(1\) 的数的个数
我们利用 \(f\) 进行快速求解，先摆出式子
记 \(tmp =\lfloor (r - l + 1)/2^{j + 1} \rfloor \times 2^{j + 1}\)
\(\displaystyle f_{l, j} - f_{l + tmp, j} + \sum_{i = l + tmp + 2^{j}}^{r}cnt_i\)
然后我们解释一下，
为啥不能直接相减
因为 \(f_{i, j}\) 中我们减去的 \(i\) 不同， 所以实际上他们没啥关系
那么那个式子在干什么，虽然不能都减去 \(l\) 但是我们只关心第 \(j\) 位的贡献，那么我们多减去几个\(2^{j + 1}\) 都无所谓，所以我们找到了最长的 \(2^{j + 1}\) 的段进行处理
这样剩下了一小段，以 \(l + tmp\)为始，发现减去 \(l + tmp\) 后该段是一个从 \(0\) 开始的序列， 根据二进制发现前 \(2^{j}\)个数第 \(j\)位为 \(0\) ，后面到\(r\)(少于 \(2^{j}\)个数)这些数该位为 \(1\) ，所以就是后面的部分
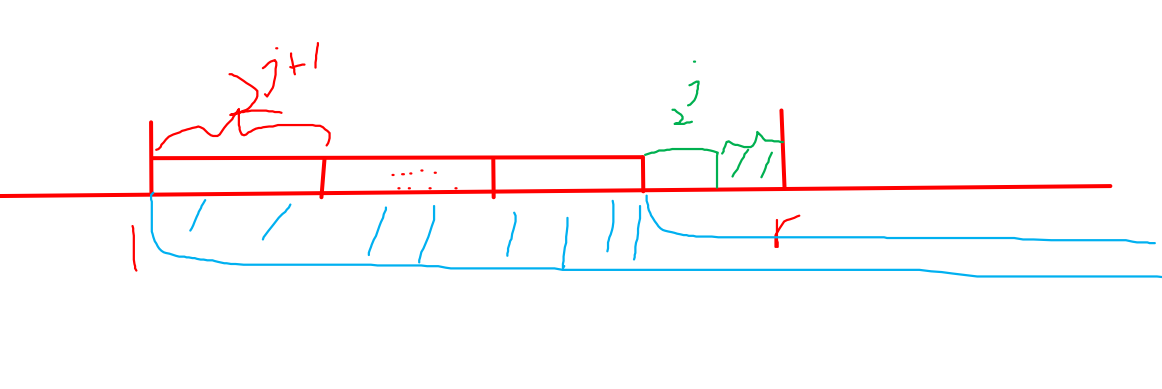
结合丑图看一下，就是 \(f\) 相减得到蓝色部分对应数轴上红色部分， 绿色前 \(2^j\) 没有贡献，后面到 \(r\)有贡献
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 500005;
inline int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = (x << 3) + (x << 1) + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
int n, cnt[maxn], f[maxn][20];
int main(){
freopen("stone.in","r",stdin);
freopen("stone.out","w",stdout);
// freopen("a.out","w",stdout);
n = read();
for(int i = 1; i <= n; ++i){
int x = read();
cnt[x] = 1 - cnt[x];
}
for(int i = 1; i <= n; ++i)cnt[i] += cnt[i - 1];
for(int i = n; i >= 0; --i)
for(int j = 0; i + (1 << j) <= n; ++j)
f[i][j] = f[min(n + 1, i + (1 << (j + 1)))][j] + cnt[min(n, i + (1 << (j + 1)) - 1)] - cnt[i + (1 << j) - 1];
int mx = log2(n);
for(int i = 1; i <= n; ++i){
int lim = n / (i + 1); bool flag = 0;
for(int j = 0; j <= mx; ++j){
int sum = 0;
for(int k = 0; k <= lim; ++k){
int l = k * (i + 1), r = min(n, (k + 1) * (i + 1) - 1), tmp = ((r - l + 1) >> (j + 1)) << (j + 1);
int now = f[l][j] - f[l + tmp][j];
if(l + tmp + (1 << j) - 1 < r)now += cnt[r] - cnt[l + tmp + (1 << j) - 1];
sum += now;
}
if(sum & 1){flag = 1;break;}
}
if(flag)printf("Alice ");
else printf("Bob ");
}
return 0;
}
B. 大鱼吃小鱼
显然每次吃能吃的最大的，一次直接吃到能吃原来第一个他吃不了的，这个过程可以用线段树二分 / 平衡树二分实现
这样每次操作完再吃一个就能扩大一倍，所以复杂度是对的
我使用了 \(FHQ\_Treap\) 二分写法，强烈推荐
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 400005;
const ll inf = 1e18 + 1e5;
inline ll read(){
ll x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = (x << 3) + (x << 1) + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
struct FHQ_Treap{
#define ls t[x].l
#define rs t[x].r
struct node{
ll val, sum;
int l, r, size, key;
}t[maxn];
int root, cnt;
int New(ll val){t[++cnt].key = rand(); t[cnt].val = t[cnt].sum = val; t[cnt].size = 1; return cnt;}
void push_up(int x){
t[x].sum = (t[ls].sum + t[rs].sum + t[x].val);
t[x].size = (t[ls].size + t[rs].size + 1);
}
void split(int x, int &l, int &r, ll val){
if(!x)return l = r = 0, void();
if(val < t[x].val){split(t[x].l, l, t[x].l, val); r = x;}
else{split(t[x].r, t[x].r, r, val); l = x;}
push_up(x);
}
void split_sum(int x, int &l, int &r, ll sum){
if(!x)return l = r = 0, void();
if(t[rs].sum >= sum){split_sum(rs, rs, r, sum); l = x; push_up(x); return;}
if(t[rs].sum + t[x].val >= sum){l = ls; r = x; t[x].l = 0; push_up(x); return;}
split_sum(ls, l, ls, sum - t[rs].sum - t[x].val);
r = x; push_up(x);
}
int merge(int x, int y){
if(!x || !y)return x | y;
if(t[x].key < t[y].key){t[x].r = merge(t[x].r, y);push_up(x);return x;}
else {t[y].l = merge(x, t[y].l); push_up(y); return y;}
}
void insert(ll val){
int l = 0, r = 0; split(root, l, r, val);
root = merge(merge(l, New(val)), r);
}
void erase(ll val){
int l = 0, m = 0, r = 0; split(root, l, r, val); split(l, l, m, val - 1);
m = merge(t[m].l, t[m].r);
root = merge(merge(l, m), r);
}
ll findmin(int x){
if(x == 0)return inf;
while(t[x].l){x = t[x].l;}
return t[x].val;
}
int dep = 0;
int solve(ll s, ll k){
if(s > k)return 0;
int l = 0, m = 0, r = 0;
split(root, l, r, s - 1);
ll nxt = min(findmin(r), k);
if(s + t[l].sum <= nxt){
root = merge(l, r);
return -1;
}
split_sum(l, l, m, nxt - s + 1);
root = merge(l, r);
int ans = t[m].size;
int down = solve(s + t[m].sum, k);
l = r = 0;
split(root, l, r, s - 1);
root = merge(merge(l, m), r);
if(down == -1)return -1;
return ans + down;
}
}t;
int n, q;
int main(){
srand(time(NULL));
freopen("fish.in","r",stdin);
freopen("fish.out","w",stdout);
n = read();
for(int i = 1; i <= n; ++i)t.insert(read());
q = read();
for(int i = 1; i <= q; ++i){
int op = read();
if(op == 1){
ll s = read(), k = read();
printf("%d\n", t.solve(s, k - 1));
}
if(op == 2)t.insert(read());
if(op == 3)t.erase(read());
}
return 0;
}
C. 黑客
此为本场真 \(T1\) ，确信
上来发现部分分极多，快速码了一个 \((b - a + 1) * (d - c + 1)\) 的
然后发现\(0 - 999\) 范围很小，于是反过来枚举一下就行了
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const ll mod = 1e9 + 7;
inline ll read(){
ll x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = (x << 3) + (x << 1) + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
ll gcd(ll a, ll b){return b ? gcd(b, a % b) : a;}
ll a, b, c, d;
int main(){
freopen("hacker.in","r",stdin);
freopen("hacker.out","w",stdout);
a = read(), b = read(), c = read(), d = read();
ll ans = 0;
for(int sum = 1; sum <= 999; ++sum){
for(int x = 1; x < sum; ++x){
int y = sum - x;
if(gcd(x, y) != 1)continue;
ll l1 = (a + x - 1) / x, l2 = (c + y - 1) / y;
ll r1 = b / x, r2 = d / y;
ll cnt = min(r1, r2) - max(l1, l2) + 1; cnt %= mod;
if(cnt > 0) ans = (ans + 1ll * cnt * sum % mod) % mod;
}
}
printf("%lld\n",ans);
return 0;
}
D. 黑客-续
上来发现是原题，回想起了被 \(TLE coders\)支配的恐惧，决定最后再打，但是除了 \(T3\) 都不会，所以来打了，然后意外的打的很顺利？
code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
inline int read(){
int x = 0; char c = getchar();
while(c < '0' || c > '9')c = getchar();
do{x = (x << 3) + (x << 1) + (c ^ 48); c = getchar();}while(c <= '9' && c >= '0');
return x;
}
const ull base = 1e17;
struct big{
ull a[105];
big operator += (const big x){
a[0] = max(a[0], x.a[0]);
for(int i = 1; i <= x.a[0]; ++i)a[i] += x.a[i];
for(int i = 1; i <= a[0]; ++i)if(a[i] >= base)++a[i + 1], a[i] -= base;
if(a[a[0] + 1])++a[0];
return (*this);
}
big operator *= (const int x){
for(int i = 1; i <= a[0]; ++i)a[i] *= x;
for(int i = 1; i <= a[0]; ++i)a[i + 1] += a[i] / base, a[i] %= base;
if(a[a[0] + 1])++a[0];
return (*this);
}
void clear(){
for(int i = 1; i <= a[0]; ++i)a[i] = 0;
a[0] = 0;
}
void print(){
printf("%llu",a[a[0]]);
for(int i = a[0] - 1; i > 0; --i)printf("%017llu",a[i]);
printf("\n");
}
}sum[2][1025], cnt[2][1025];
int n, m, k, ban[10];
big s, c;
int main(){
freopen("hacker2.in","r",stdin);
freopen("hacker2.out","w",stdout);
// freopen("d.out","w",stdout);
n = read(), m = read(), k = read();
for(int i = 1; i <= m; ++i){
int a = read(), b = read();
ban[b] |= (1 << (a - 1));
}
for(int i = 1; i <= k; ++i){
int now = (1 << (i - 1));
sum[1][now].a[0] = 1;
sum[1][now].a[1] = i;
cnt[1][now].a[0] = 1;
cnt[1][now].a[1] = 1;
}
int mx = 1 << k;
for(int i = 1; i < n; ++i){
int nt = i & 1;
for(int j = 0; j < mx; ++j){
if(cnt[nt][j].a[0]){
sum[nt][j] *= 10; big ls = cnt[nt][j];
for(int p = 1; p <= k; ++p){
if(!(ban[p] & j)){
cnt[1 - nt][j | (1 << (p - 1))] += cnt[nt][j];
sum[1 - nt][j | (1 << (p - 1))] += sum[nt][j];
sum[1 - nt][j | (1 << (p - 1))] += ls;
}
ls += cnt[nt][j];
}
cnt[nt][j].clear();
sum[nt][j].clear();
}
}
}
for(int i = 0; i < mx; ++i){
s += sum[n & 1][i];
c += cnt[n & 1][i];
}
c.print(); s.print();
return 0;
}
放在后面的前记
9.12 21:48 upd：今天写不完题解了，先放个半成品
9.13 07:40 upd : 写完了
