后缀数组SA 回文自动机PAM
后缀数组
两个数组：\(sa[]\) 和\(rk[]\)
\(sa[i]\)表示将所有后缀排第\(i\)小的后缀的编号（起始位置在哪里）
\(rk[i]\)表示以\(i\)为起始位置的后缀的排名。
这两个数组满足性质：\(sa[rk[i]]=rk[sa[i]]=i\)
oiwiki讲的很好，直接粘过来
oiwi
正常排序，帮助理解求\(sa\)过程
$nlog^2n$
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=0x3f3f3f;
const int maxn=1000005;
char s[maxn];
int n,w,sa[maxn],rk[maxn<<1|1],oldrk[maxn<<1|1];
bool cmp(int x,int y){
return rk[x]==rk[y]?rk[x+w]<rk[y+w]:rk[x]<rk[y];
//以rank[i]为第一关键字，rank[i+w]为第二关键字
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;++i)sa[i]=i;//随便给个1-n的排序
for(int i=1;i<=n;++i)rk[i]=s[i];//先按照第一个字母排个rank，只需要相对大小即可
for(w=1;w<n;w<<=1){
sort(sa+1,sa+n+1,cmp);
for(int i=1;i<=n;++i)oldrk[i]=rk[i];
for(int p=0,i=1;i<=n;++i){
if(oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w])rk[sa[i]]=p;
else rk[sa[i]]=++p;
//判断条件和p是为了去重
}
}
for(int i=1;i<=n;++i)printf("%d ",sa[i]);
return 0;
}
优化，基数排序
不卡常$nlogn$
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=0x3f3f3f;
const int maxn=1000005;
char s[maxn];
int n,w,sa[maxn],rk[maxn<<1|1],id[maxn],m=300,oldrk[maxn<<1|1],cnt[maxn];
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;++i)++cnt[rk[i]=s[i]];//按照第一个字母排个序
for(int i=1;i<=m;++i)cnt[i]+=cnt[i-1];
for(int i=n;i>=1;--i)sa[cnt[rk[i]]--]=i;
m=max(m,n);
for(w=1;w<n;w<<=1){
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;++i)id[i]=sa[i];
for(int i=1;i<=n;++i)++cnt[rk[id[i]+w]];
for(int i=1;i<=m;++i)cnt[i]+=cnt[i-1];
for(int i=n;i>=1;--i)sa[cnt[rk[id[i]+w]]--]=id[i];//基数排序第二关键字
memset(cnt,0,sizeof(cnt));
for(int i=1;i<=n;++i)id[i]=sa[i];
for(int i=1;i<=n;++i)++cnt[rk[id[i]]];
for(int i=1;i<=m;++i)cnt[i]+=cnt[i-1];
for(int i=n;i>=1;--i)sa[cnt[rk[id[i]]]--]=id[i];//基数排序第一关键字
for(int i=1;i<=n;++i)oldrk[i]=rk[i];//与之前相同
for(int p=0,i=1;i<=n;++i){
if(oldrk[sa[i]]==oldrk[sa[i-1]]&&oldrk[sa[i]+w]==oldrk[sa[i-1]+w])rk[sa[i]]=p;
else rk[sa[i]]=++p;
}
}
for(int i=1;i<=n;++i)printf("%d ",sa[i]);
return 0;
}
卡常+亿点注释
卡常$nlogn$
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int inf=0x3f3f3f;
const int maxn=1000005;
char s[maxn];
int n,w,sa[maxn],rk[maxn<<1|1],id[maxn],m=300,oldrk[maxn<<1|1],cnt[maxn],px[maxn];
bool cmp(int x,int y,int w){
return oldrk[x]==oldrk[y]&&oldrk[x+w]==oldrk[y+w];
}
int main(){
scanf("%s",s+1);
n=strlen(s+1);
for(int i=1;i<=n;++i)++cnt[rk[i]=s[i]];//按照第一个字母排个序，这个时候只需要相对大小关系，里面的东西暂时不太合法
for(int i=1;i<=m;++i)cnt[i]+=cnt[i-1];//桶累加
for(int i=n;i>=1;--i)sa[cnt[rk[i]]--]=i;//cnt[..]为i的新rank 其实是sa[rk[i]]=i
m=max(m,n);//m为桶的值域
for(w=1;w<n;w<<=1){
int p=0;
for(int i=n;i>n-w;--i)id[++p]=i;//空串直接记录，按照第二关键字他们最小且没有顺序，所以随便给个顺序即可
for(int i=1;i<=n;++i)if(sa[i]>w)id[++p]=sa[i]-w;//第二关键字，用后缀i的当前sa的顺序去更新后缀sa[i]-w
for(int i=1;i<=m;++i)cnt[i]=0;//清桶
for(int i=1;i<=n;++i)++cnt[px[i]=rk[id[i]]];//按照原来的rank排序，px临时存一下rk[id[i]]，减少不必要的内存访问
for(int i=1;i<=m;++i)cnt[i]+=cnt[i-1];//累加
for(int i=n;i>=1;--i)sa[cnt[px[i]]--]=id[i];//cnt[..]为sa[i]的新rank 而为了避免改乱，所以原来的sa用id来代替，这就是上面和这里赋值用id的原因
for(int i=1;i<=n;++i)oldrk[i]=rk[i];//copy一下，cmp用
p=0;
for(int i=1;i<=n;++i)rk[sa[i]]=cmp(sa[i],sa[i-1],w)?p:++p;//写cmp减少不必要的内存访问，去重
if(p==n)break;//已经排完就不用管了
m=p;//值域优化
}
for(int i=1;i<=n;++i)printf("%d ",sa[i]);
return 0;
}
最长公共前缀\(LCP\)
定义\(LCP(i,j)\) 表示\(sa_i\)个和\(sa_j\)个的两个后缀的最长公共前缀。
性质
\(LCP(i,j)=LCP(j,i)\)
\(LCP(i,i)=len(sa_i)=n−sa_i+1\)
\(LCP Lemma :\)
\(LCP(i,j)=min(LCP(i,k),LCP(k,j))(1≤i≤k≤j≤n)\)
\(LCP Theorem:\)
$ LCP(i,j)=min(LCP(k,k−1))(1<i<k≤j≤n)$
求法
定义
\(height[i]=lcp(sa[i],sa[i-1])\)
引理：
\(height[rk[i]]\ge height[rk[i-1]]-1\)
比较感性的证明观察一下
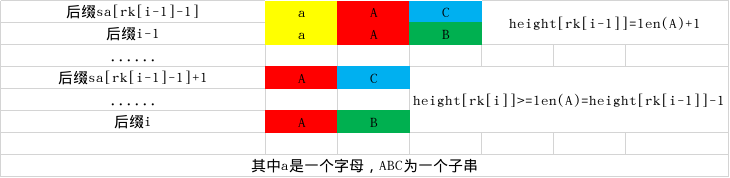
LCP
void LCP(){
for(int i=1,k=0;i<=n;++i){
if(rk[i]==0)continue;
if(k)--k;//height[i]>=heigh[i-1]-1;
while(s[i+k]==s[sa[rk[i]-1]+k])++k;
height[rk[i]]=k;
}
}
回文自动机PAM
code
#include<cstring>
#include<iostream>
using namespace std;
const int maxn = 5e5+55;
char s[maxn];
int ch[maxn][27], len[maxn], fail[maxn], dep[maxn];
int main(){
cin >> s + 1;
s[0] = '#';
int n = strlen(s + 1);
int las = 0, ans = 0, cnt = 1;
fail[0] = 1;len[1] = -1;
for(int i = 1 ; i <= n; ++i){
while(s[i - len[las] - 1] != s[i])las = fail[las];
if(!ch[las][s[i] - 'a']){
len[++cnt] = len[las] + 2;
int j = fail[las];
while(s[i - len[j] - 1] != s[i])j = fail[j];
fail[cnt] = ch[j][s[i] - 'a'];
ch[las][s[i] - 'a'] = cnt;
}
las = ch[las][s[i] - 'a'];
cout << (ans = dep[las]) << " " ;
}
return 0;
}
