NOIP提高组模拟赛12

A. 打地鼠

大水题，~~暴力比正解难系列~~

二维前缀和 $n^2$ 枚举即可

code

#include <cstring>
#include <cstdio>
using namespace std;
const int maxn=2005;
int max(int x,int y){return x>y?x:y;}
char c[maxn];
int sum[maxn][maxn];
int main(){
    int n,k;
    scanf("%d%d",&n,&k);
    for(int i=1;i<=n;++i){
        scanf("%s",c+1);
        for(int j=1;j<=n;++j)
         if(c[j]=='1')sum[i][j]=1;
    }
    for(int i=1;i<=n;++i)
      for(int j=1;j<=n;++j)
        sum[i][j]+=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
    int ans=-1;
    for(int i=k;i<=n;++i)
      for(int j=k;j<=n;++j){
          int ls=sum[i][j]-sum[i-k][j]-sum[i][j-k]+sum[i-k][j-k];
          ans=max(ans,ls);
      }
    printf("%d\n",ans);
    return 0;
}

B. 竞赛图

看到数据范围就知道是状压，然而最终只是状态+ $Tarjan$ 判断，发现 $a[i][j] xor a[j][i]=1$ 知道这应该是特殊性质，但是没有细想

状压dp，发现对一个状态的图来说，将强联通分量缩成一个点后的图中，一定有一个新的点 $x$ 连接他的所有边都指向其他强联通分量 $y$ ，没有其他强联通分量指向 $x$ 的边

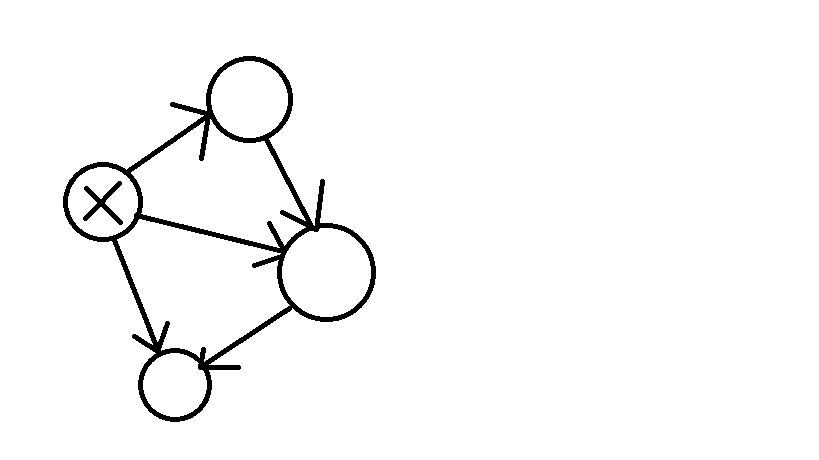
因为如果有指回 $x$ 的边，那么一定能构成新的强联通分量，或者出现新的 $x$ ，自己画几个图试试就知道了

考虑当前状态不合法的图， $x$ 与其他集合所有子集的并集都是非法的，因为没有指回 $x$ 的边，他们一定不能构成强联通分量

所有合法状态可以看做 $x$ ,能够到达的点看做 $y$ ，那么 $x$ 与 $y$ 的子集的并集都是非法状态，通过枚举 $y$ 的子集筛去不合法状态

枚举子集的方法 $for(int\;\;i=s;i;i=(i-1)\&s)$ ，将状态不停的-1，用 $\&$ 保证原来为0的位不是1

code


#include <cstring>
#include <cstdio>
using namespace std;
int n,ans;
bool flag[17000000];
int y[17000000];
inline int read(){
    char c;c=getchar();
    while(c<'0'||c>'9')c=getchar();
    int x=0;
    while(c>='0'&&c<='9'){
        x=(x<<1)+(x<<3)+c-'0';
        c=getchar();
    }
    return x;
}
int main(){
   int T;T=read();
   for(register int ask=1;ask<=T;++ask){
       n=read();ans=1<<n;
       for(register int i=0;i<=ans;++i)flag[i]=0;
       for(register int i=0;i<=ans;++i)y[i]=0;
       for(register int i=1;i<=n;++i)
         for(register int j=1;j<=n;++j)
           y[1<<(i-1)]|=(read()<<(j-1));
        for(register int i=1;i<(1<<n);++i){
            if(!y[i])y[i]=y[(i&-i)]&y[(i^(i&-i))];
            if(flag[i]){--ans;continue;}
            for(register int j=y[i];j;j=(j-1)&y[i])flag[j|i]=1;
        }
        printf("%d\n",ans);
   }
    return 0;
}

C. 糖果

又是一个奇妙的DP

考场打出了40分搜索，比枚举全排列改进的地方在于去掉了许多无用枚举，考虑该轮选择的数为 $x,y,z$ $C$ 选了 $z$ 那么 $x,y$ 在 $C$ 序列中的位置，只要不小于 $z$ 即可，可以用排列数计算， $A_{剩余位置}^2$ 然后不需要考虑这三个数递归下去，这样每轮可以去掉3个数，比起枚举全排列要快不少，~~然而还是慢的要死~~

正解DP

用到了一点上面暴力的东西，排列数，不难发现如果我们知道了 $C$ 每一轮选择了哪个数的序列，称这个选择的序列为决策序列
，那么能够取到这些数的原序列可以用排列数直接算出来

因为我们是一轮一轮考虑的，所以剩余位置是3的倍数-1，乘以 $A_2^2*A_5^2*.....A_{n-1}^2$ 就是乘以 $1*2*4*5*7*8....*(n-2)*(n-1)$

计算操作序列数就是那个神仙DP了

~~~~~~~~~~~~~~~~~~~~~~~~~

设 $f[i][j][k][1/0]$ 表示 $A$ 选到 $i$ $B$ 选到 $j$ $C$ 还有 $k$ 个备选位置，现在该A/B选数的方案数

所谓备选位置就是C之前应该向决策序列中加入数，但是还没有加入的。换种说法就是 $AB$ 决策数 $-C$ 决策数

用当前状态更新其他状态，初始 $f[1][1][0][0]=1$

~~~~~~~~~~~~~~~~~~~~~~~~~

如果 $f[i][j][k][0]\not =0$ ，当前状态存在，这是A的决策回合

如果 $a[i]$ 在 $B$ 中的位置比 $j$ 小，那么 $A$ 一定取不到该数，那么他只能尝试取第 $i+1$ 个数

$f[i][j][k][0]->f[i+1][j][k][0]$

如果 $a[i]$ 在 $B$ 中的位置大于或等于 $j$ （等于情况是状态非法，但是这里也更新，会在 $B$ 决策时丢弃）

那么可能是 $A$ 选择了这个数，这样就到了 $B$ 的回合 $f[i][j][k][0]->f[i][j][k][1]$

也可能是 $C$ 之前就选择了这个数，就是说 $C$ 的某个备选位置选择了这个数，那么 $A$ ，需要尝试取第 $i+1$ 个数，有 $k$ 种方案 $f[i][j][k][0]*k->f[i+1][j][k-1][0](k\not =0)$

~~~~~~~~~~~~~~~~~~~~~~~~~

如果 $f[i][j][k][1]\not =0$ ，当前状态存在，这是B的决策回合

如果 $b[j]$ 在 $A$ 中的位置比 $i$ 小，那么 $B$ 一定取不到该数，那么他只能尝试取第 $j+1$ 个数

$f[i][j][k][1]->f[i][j+1][k][1]$

如果 $b[j]$ 在 $A$ 中的位置大于或等于 $i$

那么 $a[i]==b[j]$ 时状态非法，舍弃，不再转移

此时 $b[j]$ 在 $A$ 中的位置大于 $i$

那么可能是 $B$ 选择了这个数，这样就到了 $C$ 的回合，不知道他选了啥，就当他选了，以后再考虑可能是啥，就是 $C$ 多了一个备选位置，并且把回合交给了 $A$ ,开始下一轮选数 $f[i][j][k][1]->f[i+1][j+1][k+1][0]$

也可能是 $C$ 之前就选择了这个数，就是说 $C$ 的某个备选位置选择了这个数，那么 $B$ 就要尝试取 $j+1$ 个数，有 $k$ 种方案 $f[i][j][k][1]*k->f[i][j+1][k-1][1](k\not =0)$

最后当状态到了 $f[n+1][n][0][0]$ 时，选数结束，记录答案

code

#include <cstring>
#include <cstdio>

using namespace std;
const int mod=1e9+7;
const int maxn=405;
int n,a[maxn],b[maxn];
int pa[maxn],pb[maxn];
long long f[maxn][maxn][151][2];
int main(){
   scanf("%d",&n);
   for(int i=1;i<=n;++i)scanf("%d",&a[i]);
   for(int i=1;i<=n;++i)scanf("%d",&b[i]);
   for(int i=1;i<=n;++i)pa[a[i]]=i;
   for(int i=1;i<=n;++i)pb[b[i]]=i;
   long long ans=0;
   f[1][1][0][0]=1;   
   for(int i=1;i<=n+1;++i)
    for(int j=1;j<=n+1;++j)
      for(int k=0;k<=n/3;++k)
      {
          if(f[i][j][k][0]){
              if(i==n+1){
                  if(!k)ans=(ans+f[i][j][k][0])%mod;
                  continue;
              }
              if(pb[a[i]]<j)f[i+1][j][k][0]=(f[i+1][j][k][0]+f[i][j][k][0])%mod;
              else{
                  f[i][j][k][1]=(f[i][j][k][1]+f[i][j][k][0])%mod;
                  if(k)f[i+1][j][k-1][0]=(f[i+1][j][k-1][0]+f[i][j][k][0]*k%mod)%mod;
              }
          }
          if(f[i][j][k][1]){
              if(pa[b[j]]<i)f[i][j+1][k][1]=(f[i][j+1][k][1]+f[i][j][k][1])%mod;
              else if(a[i]!=b[j]){
                  f[i+1][j+1][k+1][0]=(f[i+1][j+1][k+1][0]+f[i][j][k][1])%mod;
                  if(k)f[i][j+1][k-1][1]=(f[i][j+1][k-1][1]+f[i][j][k][1]*k%mod)%mod;
              }
          }
      }
    for(int i=1;i<=n;i++)
      if(i%3)ans=ans*i%mod;
    printf("%d\n",ans);
    return 0;
}

D. 树

~~大爱题解，让本来简单的题变的复杂多了~~，照着题解思路打了半天，大力考虑特殊情况，打了一堆戳，线段树打到吐，~~结果没调出来~~

观察一个奇妙的性质，如果将每次修改打一个时间戳的话，一条边连接的两个点时间戳一样的时候才是白的，否则就是黑的

开始给每个点一个不同的时间戳，操作时用新的时间戳更新，查询的话只要查区间有多少颜色段即可，就是树剖专题染色那题的写法

code

#include <cstring>
#include <cstdio>
using namespace std;
const int maxn=300005;
void swap(int &x,int &y){x=x^y;y=y^x;x=x^y;}
struct edge{
   int net,to;
}e[maxn<<1|1];
int head[maxn],tot;
void add(int u,int v){
   e[++tot].net=head[u];
   head[u]=tot;
   e[tot].to=v;
}
struct node{
    int size,son,fa,top,dep,id;
}d[maxn];
int id[maxn],cnt;
void dfs1(int x){
    d[x].size=1;
    for(int i=head[x];i;i=e[i].net){
        int v=e[i].to;
        if(v==d[x].fa)continue;
        d[v].fa=x;d[v].dep=d[x].dep+1;
        dfs1(v);
        d[x].size+=d[v].size;
        d[x].son=d[d[x].son].size>d[v].size?d[x].son:v;
    }
}
void dfs2(int x,int top){
    d[x].top=top;d[x].id=++cnt;id[cnt]=x;
    if(d[x].son)dfs2(d[x].son,top);
    for(int i=head[x];i;i=e[i].net){
        int v=e[i].to;
        if(v==d[x].fa||v==d[x].son)continue;
        dfs2(v,v);
    }
}
int n;
struct tree{
    struct tr{
        int val,lc,rc,lazy;
    };
    tr t[maxn<<2|1];
    void push_up(int x){
        t[x].val=t[x<<1].val+t[x<<1|1].val;
        if(t[x<<1].rc!=t[x<<1|1].lc)++t[x].val;
        t[x].lc=t[x<<1].lc;
        t[x].rc=t[x<<1|1].rc;
    }
    void built(int x,int l,int r){
        if(l==r){
            t[x].lc=t[x].rc=l;
            t[x].val=0;
            return;
        }
        int mid=(l+r)>>1;
        built(x<<1,l,mid);
        built(x<<1|1,mid+1,r);
        push_up(x);
    }
    void push_down(int x){
        t[x<<1].lazy=t[x<<1|1].lazy=t[x].lazy;
        t[x<<1].lc=t[x<<1|1].lc=t[x<<1].rc=t[x<<1|1].rc=t[x].lazy;
        t[x<<1].val=t[x<<1|1].val=0;
        t[x].lazy=0;
    }
    void modify(int x,int l,int r,int L,int R,int tim){
        if(L<=l&&r<=R){
            t[x].lazy=tim;
            t[x].val=0;
            t[x].lc=t[x].rc=tim;
            return;
        }
        if(t[x].lazy)push_down(x);
        int mid=(l+r)>>1;
        if(L<=mid)modify(x<<1,l,mid,L,R,tim);
        if(R>mid)modify(x<<1|1,mid+1,r,L,R,tim);
        push_up(x);
    }

    int query(int x,int l,int r,int L,int R){
        if(L<=l&&r<=R)return t[x].val;
        if(t[x].lazy)push_down(x);
        int mid=(l+r)>>1,ans=0;
        if(L<=mid)ans+=query(x<<1,l,mid,L,R);
        if(R>mid)ans+=query(x<<1|1,mid+1,r,L,R);
        if(L<=mid&&R>mid&&t[x<<1].rc!=t[x<<1|1].lc)++ans;
        return ans;
    }

    int get_col(int x,int l,int r,int pos){
        if(l==r)return t[x].lc;
        if(t[x].lazy)push_down(x);
        int mid=(l+r)>>1,ans=0;
        if(pos<=mid)return get_col(x<<1,l,mid,pos);
        else return get_col(x<<1|1,mid+1,r,pos);
    }
}T;
void modify(int u,int v,int tim){
    while(d[u].top!=d[v].top){
        if(d[d[u].top].dep<d[d[v].top].dep)swap(u,v);
        T.modify(1,1,n,d[d[u].top].id,d[u].id,tim);
        u=d[d[u].top].fa;
    }
    if(d[u].dep>d[v].dep)swap(u,v);
    T.modify(1,1,n,d[u].id,d[v].id,tim);
}
void query(int u,int v){
    int ans=0;
    while(d[u].top!=d[v].top){
        if(d[d[u].top].dep<d[d[v].top].dep)swap(u,v);
        ans+=T.query(1,1,n,d[d[u].top].id,d[u].id);
        int t1=T.get_col(1,1,n,d[d[u].top].id);
        int t2=T.get_col(1,1,n,d[d[d[u].top].fa].id);
        if(t1!=t2)++ans;
        u=d[d[u].top].fa;
    }
    if(d[u].dep>d[v].dep)swap(u,v);
    ans+=T.query(1,1,n,d[u].id,d[v].id);
    printf("%d\n",ans);
}

void pre_work(){
    d[1].dep=1;
    dfs1(1);
    dfs2(1,1);
    T.built(1,1,n);
}
void In(){
    scanf("%d",&n);
    for(int i=1;i<n;++i){
        int u,v;scanf("%d%d",&u,&v);
        add(u,v);add(v,u);
    }
}
void work(){
    int q;scanf("%d",&q);
    for(int i=1;i<=q;++i){
        int tp,x,y;
        scanf("%d%d%d",&tp,&x,&y);
        if(tp&1)modify(x,y,i+n);
        else query(x,y);
    }
}
int main(){
    In();
    pre_work();
    work();
    return 0;
}

posted @ 2022-02-13 08:02 Chen_jr 阅读(140) 评论(5) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· NOIP提高组模拟赛8

· NOIP提高组模拟赛16

· 2025/1/16 NOIP模拟赛

· NOIP 模拟赛 1~10

· 8.23 模拟赛小记

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

公告

昵称： Chen_jr
园龄： 3年2个月
粉丝： 90
关注： 69

+加关注

2025年3月

日

一

二

三

四

五

六

Chen_jr

NOIP提高组模拟赛12

A. 打地鼠

B. 竞赛图

C. 糖果

D. 树

公告

搜索

最新随笔

随笔分类 (212)

随笔档案 (212)

阅读排行榜

评论排行榜

推荐排行榜

最新评论