NOIP提高组模拟赛11
A. 玩游戏
贪心，尝试向两边扩展，能扩展到使手里的数更小的地方就扩展，直到边界处或者两边扩展不了（走不动或者不能使手里的数更小）
貌似不能贪心了？
逆向思维，假如能够扩展完，那么最终手里的数为\(sum=\sum_{i=2}^na[i]\)我们假设走出来了，从两边向里扩展，进行逆向操作（可以看做移动的撤回）如果能扩展到正向扩展的区间，那么就有解
反向扩展需要把加变成减，或者像我一样将\(sum\)取相反数，仍然加上\(a[i]\)但是要保证手里的数始终非负
code
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=100005;
long long a[maxn];
int n,k;
bool work(){
long long ls=0;
for(int i=2;i<=n;++i)ls+=a[i];
if(ls>0)return false;
int lp=k,rp=k;
long long res=0;
while(1){
bool flag=1;
if(lp>1){
long long lsum=0;int ll;
for(ll=lp;ll>1;--ll){
lsum+=a[ll];
if(lsum+res>0||lsum<=0)break;
}
if(lsum<=0){
res+=lsum;lp=ll-1;flag=0;
while(lp>1&&a[lp]<=0)res+=a[lp--];
}
}
if(rp<n){
long long rsum=0;int rr;
for(rr=rp;rr<n;++rr){
rsum+=a[rr+1];
if(rsum+res>0||rsum<=0)break;
}
if(rsum<=0){
res+=rsum;rp=rr+1;flag=0;
while(rp<n&&a[rp+1]<=0)res+=a[++rp];
}
}
if(flag)break;
}
if(lp==1&&rp==n)return true;
ls=-ls;++lp;
int pl=2,pr=n;
while(1){
bool flag=1;
if(pl<lp){
long long lsum=0;int ll;
for(ll=pl;ll<lp;++ll){
lsum+=a[ll];
if(lsum+ls<0||lsum>=0)break;
}
if(lsum>=0){
ls+=lsum;pl=ll+1;flag=0;
while(pl<lp&&a[pl]>=0)ls+=a[pl++];
}
}
if(pr>rp){
long long rsum=0;int rr;
for(rr=pr;rr>rp;--rr){
rsum+=a[rr];
if(rsum+ls<0||rsum>=0)break;
}
if(rsum>=0){
ls+=rsum;pr=rr-1;flag=0;
while(pr>rp&&a[pr]>=0)ls+=a[pr--];
}
}
if(flag)break;
}
if(pl==lp&&pr==rp)return true;
return false;
}
int main(){
int T;scanf("%d",&T);
for(int ask=1;ask<=T;++ask){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i)scanf("%lld",&a[i]);
bool flag=work();
if(flag)printf("Yes\n");
else printf("No\n");
}
return 0;
}
B. 排列
很妙的DP，题解说的什么笛卡尔树DP我完全不会
设\(dp[i][j][1/0][1/0]\)表示长度为\(i\)的区间操作至多\(j\)次只剩一个，左边界外是否存在最大值（大于区间内所有数），右边界同理
等等，有没有发现\(j\)的定义有些奇怪，为什么不直接定义成恰好操作\(j\)次呢
因为那样复杂，实际上如果那样转移的话，需要多一重枚举，直接喜提TLE，而用至多这个定义，实际上也是叫做前缀和优化
回到DP，使用拼凑的方法来求解，枚举区间内最大值在的位置\(k\)
令左区间为\(k-1\)，右区间为\(i-k\)
\(f[i][j][0][0]=\sum_{k=1}^i f[k-1][j][0][1]*f[i-k][j][1][0]*C_{i-1}^{k-1}\)
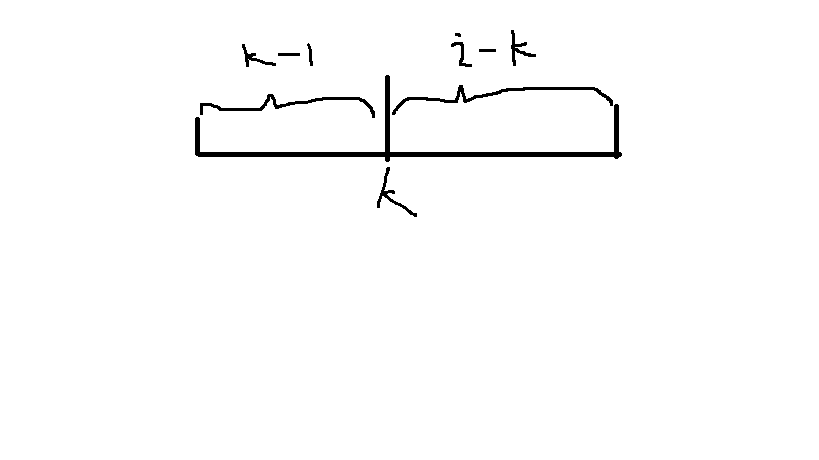
最大值在\(k\)，对左区间而言，右界外有最值，右区间的左界外有最值，除去最值外共\(i-1\)个数在两侧区间，每个区间可以是任意选择的，有\(C_{i-1}^{k-1}\)种分配方法
\(f[i][j][1][0]=\sum_{k=1}^i f[k-1][j-1][1][1]*f[i-k][j][1][0]*C_{i-1}^{k-1}\)
最大值在\(k\)，对左区间而言，两侧有最值，右区间的左界外有最值，组合意义同上，注意左区间要\(j-1\)内消完，因为最大值只有左界外最大值能消，需要消完左区间后新的一轮才能消去
\(f[i][j][0][1]=\sum_{k=1}^i f[k-1][j][0][1]*f[i-k][j-1][1][1]*C_{i-1}^{k-1}\)
类比上面
\(f[i][j][1][1]=\sum_{k=1}^i (f[k-1][j][1][1]*f[i-k][j][1][1]-(f[k-1][j][1][1]-f[k-1][j-1][1][1])*(f[i-k][j][1][1]-f[i-k][j-1][1][1]))*C_{i-1}^{k-1}\)
这种情况比较特殊，中间的最大值在\(j\)轮内消去，而两边都可以消去它，那么只需要任意一侧\(j-1\)轮内消完即可，简单容斥一下，总方案减去两边都是\(j\)轮消完的方案
最后答案就是\(f[n][k][0][0]-f[n][k-1][0][0]\)
code
#include<cstdio>
using namespace std;
const int maxn=1005;
long long n,m,mod;
long long dp[maxn][maxn][2][2];
long long c[maxn][maxn];
void get_C(int n){
for(int i=0;i<=n;++i){
c[i][0]=1;
for(int j=1;j<=i;++j)
c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&mod);
get_C(n);
for(int i=0;i<=m;++i)dp[0][i][1][1]=dp[0][i][1][0]=dp[0][i][0][1]=dp[0][i][0][0]=1;
for(int i=1;i<=n;++i)
for(int j=1;j<=m;++j)
for(int k=1;k<=i;++k){
dp[i][j][0][0]+=dp[k-1][j][0][1]*dp[i-k][j][1][0]%mod*c[i-1][k-1]%mod;
dp[i][j][0][0]%=mod;
dp[i][j][0][1]+=dp[k-1][j][0][1]*dp[i-k][j-1][1][1]%mod*c[i-1][k-1]%mod;
dp[i][j][0][1]%=mod;
dp[i][j][1][0]+=dp[k-1][j-1][1][1]*dp[i-k][j][1][0]%mod*c[i-1][k-1]%mod;
dp[i][j][1][0]%=mod;
dp[i][j][1][1]+=((dp[k-1][j][1][1]*dp[i-k][j][1][1]%mod-(((dp[k-1][j][1][1]-dp[k-1][j-1][1][1]+mod)%mod)*((dp[i-k][j][1][1]-dp[i-k][j-1][1][1]+mod)%mod)%mod)+mod)%mod)*c[i-1][k-1]%mod;
dp[i][j][1][1]%=mod;
}
printf("%lld\n",(dp[n][m][0][0]-dp[n][m-1][0][0]+mod)%mod);
return 0;
}
C. 最短路
题解做法没怎么看懂，这是另一种做法，二维\(dijkstra\)
正向反向建图\(d[x][y]\)表示正向图到\(x\)反向图到\(y\)的最短距离
使用\(bitset\)维护经过的城市，再次经过同一城市不再计算花费
（注意不是状压）
从\(d[1][1]\)出发到\(d[n][n]\)为答案
意义不难理解，正确性呢？
一种解释是，对于在正图经过的任意一个点，都在反图（也就是返回过程）中尝试走过了整张图，答案状态一定被统计到了
点击查看代码
#include<cstdio>
#include<cstring>
#include<queue>
#include<bitset>
using namespace std;
const int maxn=255;
const int maxm=80005;
const int inf=1061109567;
int read()
{
int x = 0;
char c;
while (!isdigit(c = getchar()));
do {
x = (x << 1) + (x << 3) + (c ^ 48);
}while (isdigit(c = getchar()));
return x;
}
struct edge{int net,to;};
struct G{
edge e[maxm];
int head[maxn],tot;
void add(int u,int v){
e[++tot].net=head[u];
head[u]=tot;
e[tot].to=v;
}
}G1,G2;
struct zt{
int x,y,c;
zt(){}
zt(int _x,int _y,int _c){
x=_x;
y=_y;
c=_c;
}
bool operator <(const zt &x)const{
return x.c<c;
}
};
int p[maxn],n,m;
void In(){
n=read();m=read();
for(int i=1;i<=n;++i)p[i]=read();
for(int i=1;i<=m;++i){
int u,v;u=read();v=read();
G1.add(u,v);G2.add(v,u);
}
}
int d[maxn][maxn];
bool vis[maxn][maxn];
bitset<maxn>flag[maxn][maxn];
priority_queue<zt>q;
void dij(){
memset(d,0x3f,sizeof(d));
q.push(zt(1,1,0));
d[1][1]=p[1];flag[1][1].set(1);vis[1][1]=1;
while(!q.empty()){
zt ls=q.top();q.pop();
int nx=ls.x,ny=ls.y;
if(nx==n&&ny==n)break;
for(int i=G1.head[nx];i;i=G1.e[i].net){
int v=G1.e[i].to;
int c=d[nx][ny];
if(flag[nx][ny][v]==0)c+=p[v];
if(c>=d[v][ny])continue;
d[v][ny]=c;
flag[v][ny]=flag[nx][ny];
flag[v][ny].set(v);
if(vis[v][ny])continue;
vis[v][ny]=1;
q.push(zt(v,ny,d[v][ny]));
}
for(int i=G2.head[ny];i;i=G2.e[i].net){
int v=G2.e[i].to;
int c=d[nx][ny];
if(flag[nx][ny][v]==0)c+=p[v];
if(c>=d[nx][v])continue;
d[nx][v]=c;
flag[nx][v]=flag[nx][ny];
flag[nx][v].set(v);
if(vis[nx][v])continue;
vis[nx][v]=1;
q.push(zt(nx,v,d[nx][v]));
}
}
}
void work(){
In();
dij();
if(d[n][n]==inf)printf("-1\n");
else printf("%d\n",d[n][n]);
}
int main(){
work();
return 0;
}
D. 矩形
扫描线，按照横坐标排序，扫到矩形的左边界就在纵坐标对应区间查询，如果有标记，就把对应矩形连边，查询完标记，扫到右界就去掉，用并查集维护联通块
查询，标记，删除，区间操作->线段树
注意右界不能直接清掉对应区间，判断区间内左界数为0才能清掉，多层情况时为了方便可以不改矩形编号，因为多层时矩形一定连边了，新加入的矩形与任意一个连边即可，不严格但正确
线段树细节有亿点多，恶心死我了
2022.8.12upd:mul没有用，忽略就好，感谢chino大佬指出，
还有我发现自己写的题解有时候也不说人话啊
点击查看代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=100000;
struct jz{
int r1,c1,r2,c2;
}z[maxn+5];
int n,f[maxn+5];
int fa(int x){if(f[x])return f[x]=fa(f[x]);return x;}
void hb(int x,int y){x=fa(x);y=fa(y);if(x!=y)f[x]=y;}
struct node{
int now;//当前颜色（矩形）
int val;//当前节点最大层数
int lazy;//层数变化懒标记
bool mul;//1/0 是否只有一种颜色
bool clean;//是否需要改成一种颜色
};
struct tree{
int cnt;
node t[maxn<<2|1];
void push_up(int x){
int ls=x<<1,rs=x<<1|1;
t[x].val=max(t[ls].val,t[rs].val);
if(t[ls].now==t[rs].now){
t[x].now=t[ls].now;
t[x].mul=0;
return;
}
else{
t[x].now=0;
t[x].mul=1;
return;
}
}
void push_down(int x){
int ls=x<<1,rs=x<<1|1;
if(t[x].clean){
t[ls].now=t[rs].now=t[x].now;
t[ls].clean=t[rs].clean=1;
t[ls].mul=t[rs].mul=0;
t[x].clean=0;
}
if(t[x].lazy){
t[ls].val+=t[x].lazy;t[ls].lazy+=t[x].lazy;
t[rs].val+=t[x].lazy;t[rs].lazy+=t[x].lazy;
if(!t[ls].val){t[ls].mul=t[ls].now=0;}
if(!t[rs].val){t[rs].mul=t[rs].now=0;}
t[x].lazy=0;
}
}
void add(int x,int l,int r,int L,int R,int now){
if(L<=l&&r<=R){
++t[x].val;
t[x].clean=1;
t[x].mul=0;
t[x].now=now;
++t[x].lazy;
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid)add(x<<1,l,mid,L,R,now);
if(R>mid)add(x<<1|1,mid+1,r,L,R,now);
push_up(x);
}
void jff(int x,int l,int r,int L,int R){
if(L<=l&&r<=R){
--t[x].val;
--t[x].lazy;
if(!t[x].val){t[x].clean=t[x].mul=t[x].now=t[x].val=0;}
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid)jff(x<<1,l,mid,L,R);
if(R>mid)jff(x<<1|1,mid+1,r,L,R);
push_up(x);
}
void query(int x,int l,int r,int L,int R,int now){
if(!t[x].val)return;
if(L<=l&&r<=R&&t[x].now){
hb(now,t[x].now);
return;
}
push_down(x);
int mid=(l+r)>>1;
if(L<=mid)query(x<<1,l,mid,L,R,now);
if(R>mid)query(x<<1|1,mid+1,r,L,R,now);
return;
}
}T;
int q1[maxn],q2[maxn];
bool cmp1(int x,int y){
return z[x].r1<z[y].r1;
}
bool cmp2(int x,int y){
return z[x].r2<z[y].r2;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d%d%d%d",&z[i].r1,&z[i].c1,&z[i].r2,&z[i].c2);
for(int i=1;i<=n;++i)q1[i]=q2[i]=i;
sort(q1+1,q1+n+1,cmp1);
sort(q2+1,q2+n+1,cmp2);
int maxc=-1;
for(int i=1;i<=n;++i)
maxc=max(max(z[i].c1,z[i].c2),maxc);
int p2=1;
for(int p1=1;p1<=n;++p1){
while(z[q2[p2]].r2<z[q1[p1]].r1)T.jff(1,1,maxc,z[q2[p2]].c1,z[q2[p2]].c2),++p2;
T.query(1,1,maxc,z[q1[p1]].c1,z[q1[p1]].c2,q1[p1]);
T.add(1,1,maxc,z[q1[p1]].c1,z[q1[p1]].c2,q1[p1]);
}
int ans=0;
for(int i=1;i<=n;++i)if(fa(i)==i)++ans;
printf("%d\n",ans);
return 0;
}
