tensorflow学习5----变量管理
---恢复内容开始---
前面,读书笔记用加入正则化损失模型效果带来的提升要相对显著。
变量管理:
目的:当神经网络的结构更加复杂,参数更多的时候,就需要一个更好的方式来管理神经网络中的参数。
解决方法:提供了通过变量名称来创建或者获取一个变量的机制。
作用:在不同的函数可以通过变量的名字来使用变量。而不需要通过参数进行传递。
主要函数:
1 tf.variable_scope() 2 tf.get_variable()
1 tf.get_variable() #创建和获取变量。 2 #在创建变量时,tf.get_variable()和tf.Variable() 等价。 3 4 v=tf.get_variable(“v”,shape=[1],initializer=tf.constant_initializer(1.0)) 5 6 v=tf.Variable(tf.constant(1.0,shape=[1]),name="v")
tf.get_variable()里面,name="v",shape=[1],initializer=tf.canstant_initializer(1.0)等变量初始化函数。
如:initializer=tf.truncated_normal_initializer(stddev=0.02) :将变量初始化为满足正态分布的随机值,如果随机出来的值偏离平均值超过两个标准差,那么重新随机------>主要参数为均值和标准差。 如这里的stddev就是标准差。
卷积神经网络:
相邻两层之间只有部分的节点相连,为了展示每一层神经元的维度,一般会把每一层卷积层的节点组织成一个三维矩阵。
全连接层的缺点:当参数过多,参数增加回=会导致计算的缓慢,也容易出现过拟合。
卷积神经网络的流程:
1.输入层:组织成一个三维矩阵,一般为输入层,三维矩阵的长和宽代表图像的大小,而三维矩阵的深度代表channel。
2.卷积层:卷积层的每一个节点的输入只是上一层神经网络的一小块,这个小块通常为3*3、5*5,卷积层试图将神经网络的每一块更加深入的分析而得到抽象程度更高的特征。
一般来说,卷积层处理后。节点矩阵的深度会增加。
3.池化层(pooling):池化层不会改变三维矩阵的深度,而是缩小矩阵的大小。池化操作可以认为将一张分辨率较高的图片。
卷积层:比较重要的是一个结构------>filter:可以将当前神经网络上的子节点矩阵转换为下一层神经网路上的一个单位节点矩阵,单位节点矩阵指的是长和宽都为1,但是深度不限的节点矩阵。
filter的长和宽是人为指定的,filter的尺寸通常为3*3或5*5,同时需要指定处理的得到的单位节点矩阵的深度。

标准的计算方程还是:f(x*w+b)----->只不过对
于卷积运算的话是channel个乘以对应的权重,最后add一个biases。
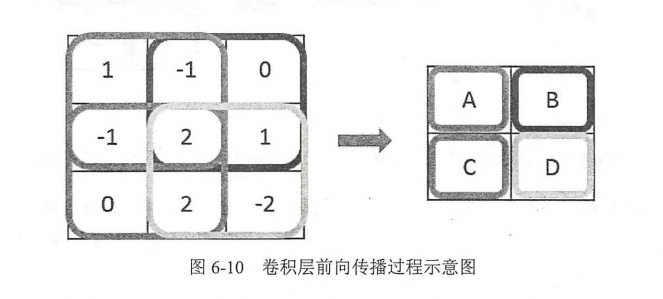
卷积神经网络的前向传播过程:
尺寸变化了,但是在当前矩阵的边界上加入全0填充后,可以保持前向传播的结果和当前层的矩阵保持一致。
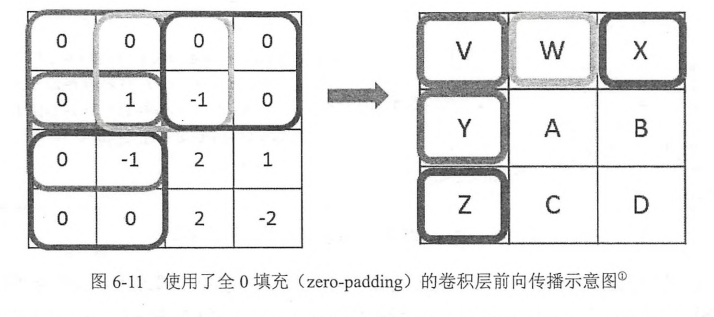
padding到0后,当前层神经网络的长和宽与filer的尺寸可以决定输出层矩阵的长和宽。


共享filter的参数,可以巨幅减少神经网络上的参数
卷积神经网路的code:
1 filter_weights=tf.get_variable('weights',shape=[5,5,3,16],initializer=tf.truncated_normal_initializer(stddev=0.1)) 2 #shpae的四维矩阵,前两个为filter的尺寸,第三个为当前层的深度,第四个为过滤器的深度,即得到的前向传播层的深度。 3 biases=tf.get_variable('biases',shape=[16],initializer=tf.constant_initializer(0.1)) 4 #biases的声明,与前向传播的深度一致。 5 conv=tf.nn.conv2d(input,filter=filter_weights,strides=[1,1,1,1],padding='SAME') 6 #tf.nn.conv2d实现卷积层前向传播。 7 #注意这个input为一个四维的矩阵,第一维对应每个输入batch, 8 #input[0,:,:,:]表示第一张图片,input=images、 9 #第三个数组,stride,为四维,要求第一维和最后一维都必须为1。 10 #最后一维为填充的方法,padding method,提供了SAME和VALID两种选择。 SAME为全零填充,VALID为不添加。 12 bias=tf.nn.bias_add(conv,bisas) 13 #tf.nn_bias_add 每个节点加上bias 14 actived_conv=tf.nn.relu(bias) 15 #将计算的结果通过RELU激活函数去
池化(pooling)
目的(object):有效减少矩阵的尺寸。可以减小最后全连接层的参数的个数。同时。可以加快计算的速度,也有防止过拟合的作用。
步骤(procedure):也类似于过滤器的结构,只不过不是加权和而是采用更加简单的最大值和平均值。
包括(including):1.最大值 操作的池化层----->max pooling (using) 2.平均值操作的pooling, (average pooling)
参数设置:与convolution相似
区别:卷积层的过滤器横跨整个深度。而池化层的过滤器只影响一个深度上的节点。所以池化层的filter除了在长和宽的两个维度移动之外,还需要在深度这个维度进行移动。
注意:池化层的目的是减小矩阵的长和宽,一般不减小矩阵的深度。
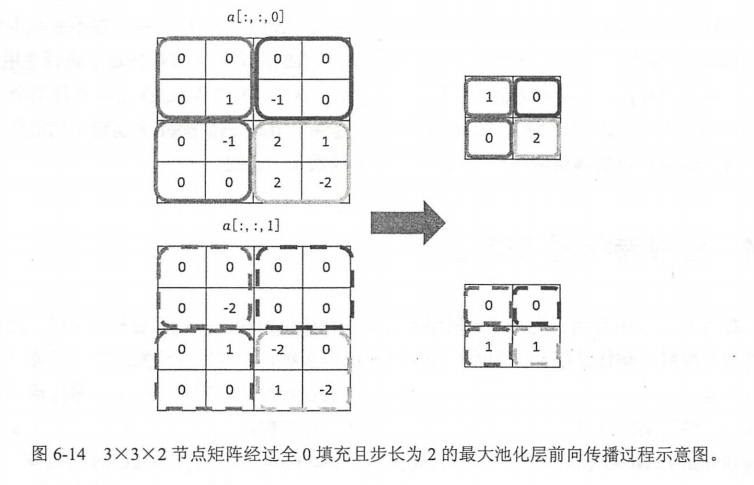
pool_code:
pool=tf.nn.max_pool(actived_conv,ksize=[1,3,3,1],strides=[1,2,2,1],padding='SAME')
#tf.nn.max_pool实现最大池化层的前向传播过程。
#ksize提供了filter的尺寸,strides提供了步长的信息,padding提供是否zero_padding
#filter的尺寸,第一个和最后一个必须z1i用得最多的是[1,2,2,1]和[1,3,3,1]
#strides同样第一维和最后一维必须为1,
tf.nn.max_pool()最大池化层,tf.nn.avg_pool()平均池化层。