tensorflow学习2-线性拟合和神经网路拟合

线性拟合的思路：

线性拟合代码：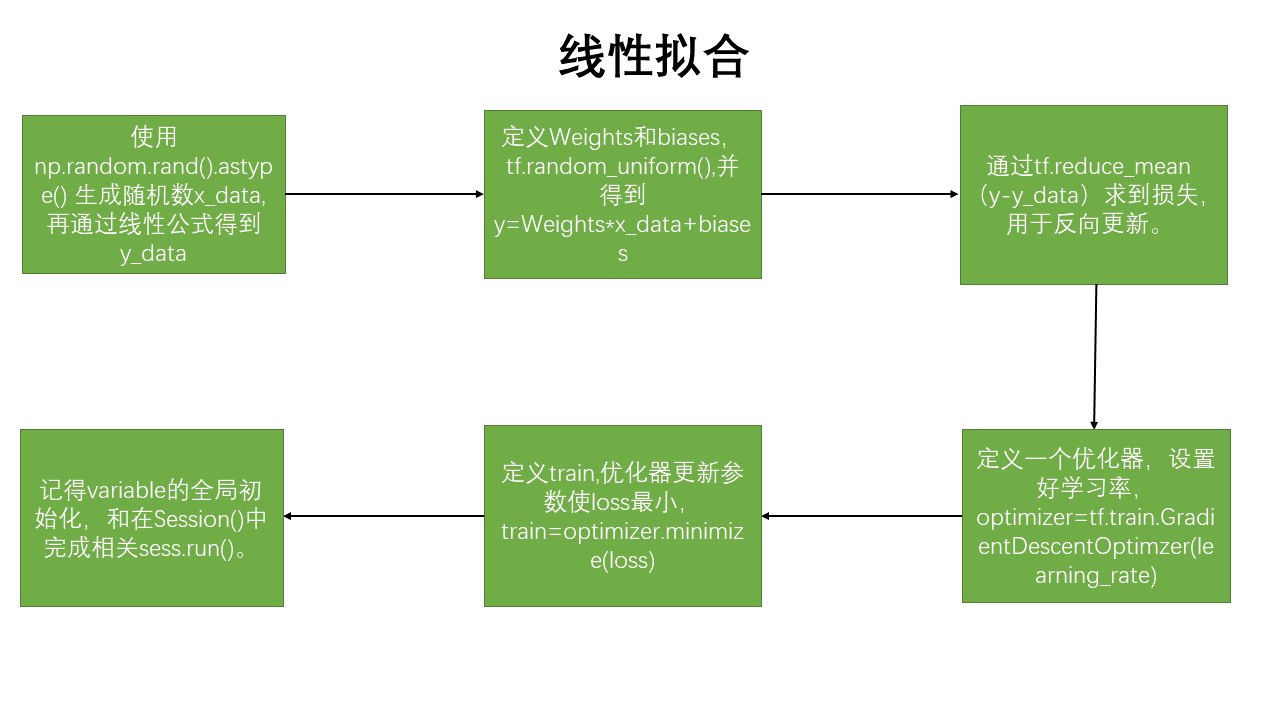

import tensorflow as tf
import numpy as np
import matplotlib.pyplot  as plt
#%%图形绘制
def data_show(x,y,w,b):
    plt.figure()
    plt.scatter(x,y,marker='.')
    plt.scatter(x,(w*x+b),marker='.')
    plt.show()
#%%生成数据
x_data=np.random.rand(100).astype(np.float32)
y_data=0.1*x_data + 0.3
#%%创建结构
Weights=tf.Variable(tf.random_uniform([1],-1.0,1.0))#平均分布的随机数
biases=tf.Variable(tf.zeros([1]))
y=Weights*x_data+biases
loss=tf.reduce_mean(tf.square(y-y_data)) #损失函数，reduce_mean:计算一个张量的各维度的元素的均值
optimizer=tf.train.GradientDescentOptimizer(0.5)#优化器 学习率选择#.GradientDescentOptimizer()实现梯度下降算法的优化器。
train=optimizer.minimize(loss)#优化器优化目标选择,使loss 最小
init=tf.global_variables_initializer() #初始化全变量节点
#%%
###训练部分
with tf.Session() as sess:
    sess.run(init)
    for i in range(200):
        sess.run(train)
        if i %20==0:
            print(i,sess.run(Weights),sess.run(biases))
            data_show(x_data,y_data,sess.run(Weights),sess.run(biases))
#%%     
            writer=tf.summary.FileWriter("/path/to/logs",tf.get_default_graph())
            writer.close()

 

 

---

 

 神经网络拟合二次函数（带噪声）

 代码：

import tensorflow as tf
import numpy as np
#%% 
def add_layer(input,in_size,out_size,activation_function=None):
    Weights=tf.Variable(tf.random_normal([in_size,out_size]))
    #tf.random.uniform()均匀分布，tf.random.normal() 正太分布
    biases=tf.Variable(tf.zeros([1,out_size])+0.1)#biases 的维度是1行，Weights的列
    #输入是1*input,Weights是input*output,output是1*output,所以biases是1*output
    wx_plus_b=tf.matmul(input,Weights)+biases
    if activation_function==None:
        output=wx_plus_b
    else:#加入激活函数
        output= activation_function(wx_plus_b)
    return output#返回output 
#%%
x_data= np.linspace(-1,1,300)[:,np.newaxis]  #np.linspace(),-1到1进行300等分的数组得到1*300，再进行变换为300*1
noise=np.random.normal(0,0.05,x_data.shape)
y_data=np.square(x_data)-0.5+noise
#%%
#占位符，feed_dict={}进行赋值
xs=tf.placeholder(tf.float32,[None,1])
ys=tf.placeholder(tf.float32,[None,1])
ll=add_layer(xs,1,10,activation_function=tf.nn.relu)#激活函数是relu
prediction=add_layer(ll,10,1,activation_function=None)
reduce_sum=tf.reduce_sum(tf.square(ys-prediction),reduction_indices=1)
loss=tf.reduce_mean(reduce_sum)
#tf.reduce_sum:计算一个张量的各个维度的元素之和。
#tf.reduce_mean()：取平均值。
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
init=tf.global_variables_initializer()
with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        sess.run(train_step,feed_dict={xs:x_data,ys:y_data})
        #if i % 50 ==0:
        #    print(sess.run(loss,feed_dict={xs:x_data,ys:y_data}))
        if i==999:
            print(sess.run(tf.square(ys - prediction),feed_dict={xs:x_data,ys:y_data}))
        #输出的是300行1列 [300,1]
        #[[  4.99251783e-02]
        #[  1.65489316e-02]
        #        ..........
        #[  3.05732153e-02]]
#经过，tf.reduce_sum(,reduction_indices=1)后为了：
        if i==999:
             print(sess.run(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=1), feed_dict={xs: x_data, ys: y_data}))
        #输出的是1行300列[300]------>[1,2,3,.....]就叫做[300],共计300个元素
        #[  3.73238046e-03  ..... 1.45917088e-02]

 

---

    补充知识 ：

1.tf.random.uniform() 符合均匀分布--------tf.random.normal()  符合正太分布

2.np.newaxis补充知识  ：

import numpy as np
a=np.array([1,2,3,4,5])#creat a array
b=a[:,np.newaxis]
#a---->[1,2,3,4,5]
#b---->[[1],[2],[3],[4],[5]] 5行1列 （5，1）
c=a[np.newaxis,:]
#c---->[[1,2,3,4,5]]  1行5列 （1，5）

3.特别注意：reduction_indices=[1]可知是指定操作坐标轴的函数，即把[300,1]按行求和后拼接为新的数组，也就是[300]的尺寸