Dynamic Filter Networks

传统的卷积网络, filter在训练后一般是恒定不变的, 相反, 这篇中引入了动态filter网络的概念, 根据输入条件动态的产生filer, 使得filter具有了自适应的能力,

包括两个部分:滤波器产生网络和 动态滤波层 这两个部分的输入可以相等或者不相等

 

 

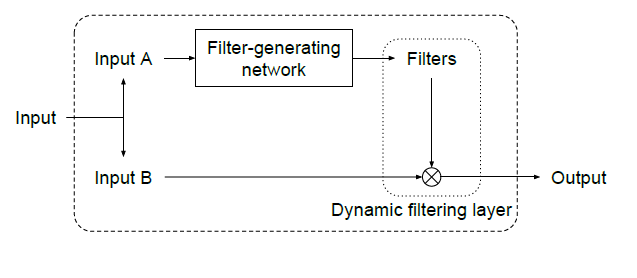
 其中需要指出的包括两个部分:

1. 模型参数(model parameters): 模型参数表示只在训练过程中被更新,在预先被初始化的层参数, 对于所有的样本都是相同的,

2. 动态产生参数(dynamically generated parameters) :是由样本所决定的, 是动态生成的，不需要初始化. filter-generating 网络输出动态产生参数

, 同时该网络还是有一部分的模型参数.

Filter-Generating Network

filter-generating 网络的输入是$I_{A} \in \mathbb{R}^{h \times w \times c_{A}}$,  输出参数$\Theta \in \mathbb{R}^{s \times s \times c_{B} \times n \times d}$ 其中 s是filter的大小, $C_{B]$是输入B的通道数. n 是filter的个数, 动态卷积d = 1，动态局部滤波d = h*w.

这个滤波器被应用于输入$I_{B} \in \mathbb{R}^{h\times w \times c_{B}}$ 产生输出 $G= F_{\theta}(I_{B})$, 其中

$G \in  \mathbb{R}^{h\times w \times n}$

} $, 过滤器大小s决定接受域，根据应用选择合适的s, 感知域的大小能够通过堆叠多个动态filter 模块进行增加:

$G(i,j) = F_{\theta}(I_{B}(i,j))$

 

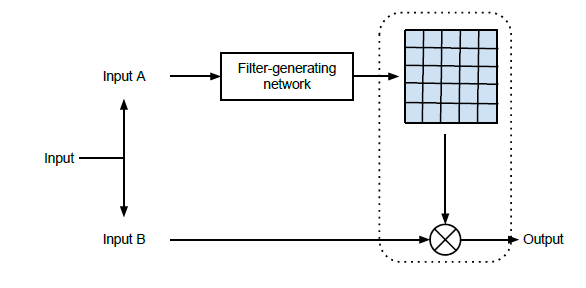
 如图所示为动态卷积的过程,