Graph-GraphSage
MPNN很好地概括了空域卷积的过程,但定义在这个框架下的所有模型都有一个共同的缺陷:
1. 卷积操作针对的对象是整张图,也就意味着要将所有结点放入内存/显存中,才能进行卷积操作。但对实际场景中的大规模图而言,整个图上的卷积操作并不现实。GraphSage[2]提出的动机之一就是解决这个问题。从该方法的名字我们也能看出,区别于传统的全图卷积,GraphSage利用采样(Sample)部分结点的方式进行学习。当然,即使不需要整张图同时卷积,GraphSage仍然需要聚合邻居结点的信息,即论文中定义的aggregate的操作。这种操作类似于MPNN中的消息传递过程。
2. 之前的方法是固有的直推式得到node embeddeding,不能泛化,无法有效适应动态图中新增节点的特性, 往往需要从头训练或至少局部重训练。
3 缺乏权值共享(Deepwalk, LINE, node2vec)。节点的embedding直接是一个N*d的矩阵, 互相之间没有共享学习参数。
4.输入维度固定为|V|。无论是基于skip-gram的浅层模型还是基于autoencoder的深层模型,输入的维度都是点集的大小。训练过程依赖点集信息的固定网络结构限制了模型泛化到动态图的能力,无法为新加入节点生成embedding。
GraphSage 的模型

文中不是对每个顶点都训练一个单独的embeddding向量,而是训练了一组aggregator functions,这些函数学习如何从一个顶点的局部邻居聚合特征信息(见图1)。每个聚合函数从一个顶点的不同的hops或者说不同的搜索深度聚合信息。测试或是推断的时候,使用训练好的系统,通过学习到的聚合函数来对完全未见过的顶点生成embedding。
一种邻居特征聚集的方法:
1.邻居采样(sample neighborhood)。因为每个节点的度是不一致的,为了计算高效, 为每个节点采样固定数量的邻居。
2.邻居特征聚集(aggregate feature information from neighbors)。通过聚集采样到的邻居特征,更新当前节点的特征。网络第k层聚集到的 邻居即为BFS过程第k层的邻居
3. 训练。既可以用获得的embedding预测节点的上下文信息(context),也可以利用embedding做有监督训练。
采样方法:
- 在图中随机采样若干个结点,结点数为传统任务中的
batch_size。对于每个结点,随机选择固定数目的邻居结点(receptive field)(这里邻居不一定是一阶邻居,也可以是二阶邻居)构成进行卷积操作的图。 - 将邻居结点的信息通过aggregate函数聚合起来更新刚才采样的结点。
- 计算采样结点处的损失。如果是无监督任务,我们希望图上邻居结点的编码相似;如果是监督任务,即可根据具体结点的任务标签计算损失
arrregate函数的选择等:
1.在实践中,每个节点的receptive field设置为固定大小,且使用了均匀采样方法简化邻居选择过程。
2.作者设计了四种不同的聚集策略,分别是Mean、GCN、LSTM、MaxPooling。
就aggretor是GCN, 图卷积聚集W(PX),W为参数矩阵,P为邻接矩阵的对称归一化矩阵,X为节点特征矩阵。
GraphSage的状态更新公式如下(下式的aggregator 是GCN, 也可以是maxpooling arregator mean aggregator):
\mathbf{h}_{v}^{l+1}=\sigma(\mathbf{W}^{l+1}\cdot aggregate(\mathbf{h}_v^l,\{\mathbf{h}_u^l\}),{\forall}u{\in}ne[v])
|
算法:

第四行表示节点vvv的任意相邻节点的聚合信息的集合;
$h_{N(v)}^{k}$表示从节点$v$的相邻节点获取的信息。
AGGGEGATE表示聚合函数;
第5行,将从相邻节点获取的信息和和这个节点自身的信息,进行拼接;
可以发现,对一个新加入的节点a,只需要知道其自身特征和相邻节点,就可以得到其向量表示。不必重新训练得到其他所有节点的向量表示。当然也可以选择重新训练。但是需要保存所有节点深度为k的表示,
这个算法直观的想法是,每次迭代,或者说每个深度,节点从相邻节点获得信息。随着迭代次数的增多,节点增量地从图中的更远处获得更多的信息。
graphSAGE并不是使用全部的相邻节点,而是做了固定尺寸的采样
既然新增的节点,一定会改变原有节点的表示,那么为什么一定要得到每个节点的一个固定的表示呢?何不直接学习一种节点的表示方法。去学习一个节点的信息是怎么通过其邻居节点的特征聚合而来的。 学习到了这样的“聚合函数”,而我们本身就已知各个节点的特征和邻居关系,我们就可以很方便地得到一个新节点的表示了
GraphSAGE的核心:GraphSAGE不是试图学习一个图上所有node的embedding,而是学习一个为每个node产生embedding的映射
训练相关:
1.为了将算法1扩展到minibatch环境上,给定一组输入顶点,先采样采出需要的邻居集合(直到深度K),然后运行内部循环(算法1的第三行)。
2.出于对计算效率的考虑,对每个顶点采样一定数量的邻居顶点作为待聚合信息的顶点。设需要的邻居数量,即采样数量为S,若顶点邻居数少于S,则采用有放回的抽样方法,直到采样出SSS个顶点。若顶点邻居数大于SSS,则采用无放回的抽样。(即采用有放回的重采样/负采样方法达到S)
3.文中在较大的数据集上实验。因此,统一采样一个固定大小的邻域集,以保持每个batch的计算占用空间是固定的(即 graphSAGE并不是使用全部的相邻节点,而是做了固定size的采样)。
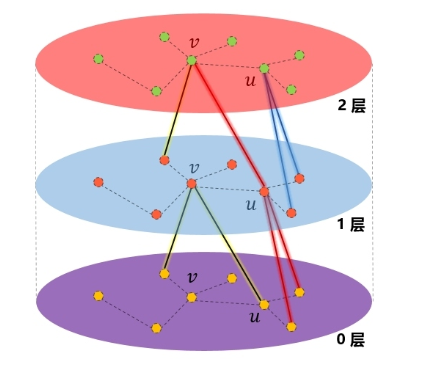
4.这里需要注意的是,每一层的node的表示都是由上一层生成的,跟本层的其他节点无关,这也是一种基于层的采样方式。
5.在图中的“1层”,节点v聚合了“0层”的两个邻居的信息,v的邻居u也是聚合了“0层”的两个邻居的信息。到了“2层”,可以看到节点v通过“1层”的节点u,扩展到了“0层”的二阶邻居节点。因此,在聚合时,聚合K次,就可以扩展到K阶邻居。
6.邻居的定义:那就是如何选择一个节点的邻居以及多远的邻居。这里作者的做法是设置一个定值,每次选择邻居的时候就是从周围的直接邻居(一阶邻居)中均匀地采样固定个数个邻居。
那我就有一个疑问了?每次都只是从其一阶邻居聚合信息,为何作者说:随着迭代,可以聚合越来越远距离的信息呢?
后来我想了想,发现确实是这样的。虽然在聚合时仅仅聚合了一个节点邻居的信息,但该节点的邻居,也聚合了其邻居的信息,这样,在下一次聚合时,该节点就会接收到其邻居的邻居的信息,也就是聚合到了二阶邻居的信息了。还是拿出我的看家本领——用图说话:
在GraphSAGE的实践中,作者发现,K不必取很大的值,当K=2时,效果就灰常好了,也就是只用扩展到2阶邻居即可。至于邻居的个数,文中提到S1×S2<=500,即两次扩展的邻居数之际小于500,大约每次只需要扩展20来个邻居即可。
这也是合情合理,例如在现实生活中,对你影响最大就是亲朋好友,这些属于一阶邻居,然后可能你偶尔从他们口中听说一些他们的同事、朋友的一些故事,这些会对你产生一定的影响,这些人就属于二阶邻居。但是到了三阶,可能基本对你不会产生什么影响了,例如你听你同学说他同学听说她同学的什么事迹,是不是很绕口,绕口就对了,因为你基本不会听到这样的故事,你所接触到的、听到的、看到的,基本都在“二阶”的范围之内。
7.没有这种采样,单个batch的内存和预期运行时是不可预测的,在最坏的情况下是O(∣V∣)O(|\mathcal{V}|)O(∣V∣)。
8.实验发现,K不必取很大的值,当K=2时,效果就很好了。至于邻居的个数,文中提到S1⋅S2≤500,即两次扩展的邻居数之际小于500,大约每次只需要扩展20来个邻居时获得较高的性能。
论文里说固定长度的随机游走其实就是随机选择了固定数量的邻居.
聚合函数选取
在图中顶点的邻居是无序的,所以希望构造出的聚合函数是对称的(即也就是对它输入的各种排列,函数的输出结果不变),同时具有较高的表达能力。 聚合函数的对称性(symmetry property)确保了神经网络模型可以被训练且可以应用于任意顺序的顶点邻居特征集合上。
Mean aggregator
mean aggregator将目标顶点和邻居顶点的第k−1层向量拼接起来,然后对向量的每个维度进行求均值的操作,将得到的结果做一次非线性变换产生目标顶点的第k层表示向量。
文中用下面的式子替换算法1中的4行和5行得到GCN的inductive变形: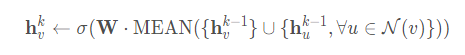
1. 均值聚合近似等价在transducttive GCN框架[Semi-supervised classification with graph convolutional networks. In ICLR, 2016]中的卷积传播规则
2.文中称这个修改后的基于均值的聚合器是convolutional的,这个卷积聚合器和文中的其他聚合器的重要不同在于它没有算法1中第5行的CONCAT操作——卷积聚合器没有将顶点前一层的表示
和聚合的邻居向量.
3.拼接操作可以看作一个是GraphSAGE算法在不同的搜索深度或层之间的简单的skip connection[Identity mappings in deep residual networks]的形式,它使得模型获得了巨大的提升
4.举个简单例子,比如一个节点的3个邻居的embedding分别为[1,2,3,4],[2,3,4,5],[3,4,5,6]按照每一维分别求均值就得到了聚合后的邻居embedding为[2,3,4,5]
Mean aggregator
Pooling聚合器,它既是对称的,又是可训练的。Pooling aggregator 先对目标顶点的邻居顶点的embedding向量进行一次非线性变换,之后进行一次pooling操作(max pooling or mean pooling),将得到结果与目标顶点的表示向量拼接,最后再经过一次非线性变换得到目标顶点的第k层表示向量.
1.max表示element-wise最大值操作,取每个特征的最大值
2.$\sigma$是非线性激活函数
3.所有相邻节点的向量共享权重,先经过一个非线性全连接层,然后做max-pooling
4.按维度应用 max/mean pooling,可以捕获邻居集上在某一个维度的突出的/综合的表现。
参数学习
基于图的损失函数倾向于使得相邻的顶点有相似的表示,但这会使相互远离的顶点的表示差异变大:
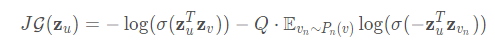
1.$Z_{u}$为节点$u$通过GraphSAGE生成的embedding
2.节点v是节点u随机游走到达的邻居
3.$\sigma$是sigmoid
4.Q是负样本的数目
5.embedding 之间的相似度通过向量点积计算
文中输入到损失函数的表示$z_{u}$是从包含一个顶点局部邻居的特征生成出来的,
而不像之前的那些方法(如DeepWalk),对每个顶点训练一个独一无二的embedding,
然后简单进行一个embedding查找操作得到.
基于图的有监督损失---------------可使用交叉熵或者范数计算
通过前向传播得到节点u的embedding $z_{u}$,然后梯度下降(实现使用Adam优化器) 进行反向传播优化参数
$W^{k}$和聚合函数内的参数。
新节点embedding的生成
这个$W^{k}$就是dynamic embedding的核心,因为保存下来了从节点原始的高维特征生成低维embedding的方式。现在,如果想得到一个点的embedding,只需要输入节点的特征向量,经过卷积(利用已经训练好的$W^{k}$以及特定聚合函数聚合neighbor的属性信息),就产生了节点的embedding。
GraphSAGE的核心:GraphSAGE不是试图学习一个图上所有node的embedding,而是学习一个为每个node产生embedding的映射
为什么GCN是transductive,为啥要把所有节点放在一起训练?
不一定要把所有节点放在一起训练,一个个节点放进去训练也是可以的。无非是如果想得到所有节点的embedding,那么GCN可以把整个graph丢进去,直接得到embedding,还可以直接进行节点分类、边的预测等任务。
其实,通过GraphSAGE得到的节点的embedding,在增加了新的节点之后,旧的节点也需要更新,这个是无法避免的,因为,新增加点意味着环境变了,那之前的节点的表示自然也应该有所调整。只不过,对于老节点,可能新增一个节点对其影响微乎其微,所以可以暂且使用原来的embedding,但如果新增了很多,极大地改变的原有的graph结构,那么就只能全部更新一次了。从这个角度去想的话,似乎GraphSAGE也不是什么“神仙”方法,只不过生成新节点embedding的过程,实施起来相比于GCN更加灵活方便了。在学习到了各种的聚合函数之后,其实就不用去计算所有节点的embedding,而是需要去考察哪些节点,就现场去计算,这种方法的迁移能力也很强,在一个graph上学得了节点的聚合方法,到另一个新的类似的graph上就可以直接使用了.
核心思想:
去学习一个节点的信息是怎么通过其邻居节点的特征聚合而来的。学习到了这样的“聚合函数”,而我们本身就已知各个节点的特征和邻居关系,我们就可以很方便地得到一个新节点的表示了。
GCN等transductive的方法,学到的是每个节点的一个唯一确定的embedding;而GraphSAGE方法学到的node embedding,是根据node的邻居关系的变化而变化的,也就是说,即使是旧的node,如果建立了一些新的link,那么其对应的embedding也会变化,而且也很方便地学到。



