论文解读《Learning Deep CNN Denoiser Prior for Image Restoration》
CVPR2017的一篇论文
Learning Deep CNN Denoiser Prior for Image Restoration:
一般的,image restoration(IR)任务旨在从观察的退化变量$y$(退化模型,如式子1)中,恢复潜在的干净图像$x$
$y \text{} =\text{}\textbf{H}x\text{}+\text{}v $
where $\textbf{H}$denotes 退化矩阵,$\textbf{v}$denotes 加性高斯白噪声(additive white Gaussian noise) with 标准差$\sigma$
指定不同的退化矩阵$\textbf{H}$,对应着不同的IR任务:
-- 当$\textbf{H}$是一个恒等矩阵,IR任务对应着图像去噪(image denoising)
-- 当$\textbf{H}$是一个模糊算子(blurring operator),IR任务对应着图像去模糊(image deblurring)
-- 当$\textbf{H}$是一个模糊和下采样的复合算子(composite operator of blurring and down-sampling),IR任务对应着图像超分辨率(image super-resolution)
IR 是一个病态逆问题(ill-posed inverse problem),先验(prior)被叫做正则化项(regularization),需要被采取去约束解决空间. 从贝叶斯的观点, 需要被推导出的潜在的干净图像$\hat{x}$能够通过解决一个MAP(maximum A posteriori )问题得到:
$\hat{x}\text{}=\text{}$ argmax$_x \text{}$log$p(\textbf{y}|\textbf{x})\text{}+\text{}$log$p(\textbf{x})\text{}\text{}\text{}(1)$
其中log$p(\textbf{y}|\textbf{x})$代表着$y$的log-似然,log$p(x)$是$x$的先验,更加正式的,公式一 被重新写:
$\hat{x} = $argmin$_{x}\frac{1}{2}||\textbf{y} - \textbf{H}x||^{2} + \lambda\Phi(x)\text{}\text{}\text{}(2)$
其中解法是最小化一个能量函数,由三个部分组成 数据保真项=$\frac{1}{2}||y\text{}\text{}-\textbf{H}x||^{2}$,一个正则化项$\Phi(x)$ 和一个平衡(trade-off)参数$\lambda$. 数据保真项确保了这个解法是通过了这个退化过程,正则化项强制执行输出所需的属性;
To solve Eqn.(2) , have two main categories methods:
--model-based optimization methods: aim to directly solve Eqn2 使用一些耗时的迭代传播(time-comsuming iterative inference)
--discriminative learning methods: 通过优化包含退化干净(degraded-clean pairs )图像对的训练集上的损失函数来学习先验参数$\Theta$和紧凑(compact)推理,目标被给出:
min$_{\Theta}\text{}\textit{l}(\hat{x},x)$ $s.t.$ $\hat{x}\text{}=\text{}$arg min$_{x}\frac{1}{2}||y - \textbf{H}x||\text{}+\text{}\lambda\Phi(x;\Theta))$ (3)
因为这个推理是被MAP估计所指导,所以我们将这种方法称作为MAP推理指导的判别式学习方法(MAP inference guided discriminative learning method);
使用一个预先定义的非线性函数:
$\hat{x}\text{}\text{}f(y,\textbf{H};\Theta)$==》注意这种函数内分号的形式,$\Theta$只是参数,前面那个才是真正的自变量,f(x;θ)是关于x的函数,其中θ是参数,x才是自变量,所以f(x;θ)是关于x的一元函数.
来替换MAP推理,我们可以把朴素的判别学习方法看作是Eqn3的一般情况。
--model-based optimization methods: 通过指定退化矩阵$\textbf{H}$来灵活的处理不同的IR任务
--discriminative learning methods: 通过使用确定的退化矩阵训练数据来学习模型
SO====》由以上两点可以得到,判别式学习方法常常限定在一些特定的任务如 MLP SRCNN DCNN;
图像降噪认为model-based method 能够处理不同噪声水平的图像,如BM3D WNNM, 然而判别学习方法只能够针对不同的噪声水平训练不同的模型。
使用判别式学习方法的优缺点:
缺点: 灵活性较差
优点: 快速的测试速度; 由于联合优化(joint optimization)和端到端的训练(end-to-end training),具有前景性的表现;
使用model-based optimization 方法的优缺点:
缺点:时间消耗time-consuming with 复杂的先验 sophisticated prior 为了好的表现.
SO ===》 非常有吸引力的是利用他们各自的优点去研究他们的集成
Method
在变量分割技术的辅助下,如交替方向乘子法(alternating direction method of multiplier,ADMM)和半二次分割法(half quadratic splitting),使得有可能独立的处理 保真项(fidelity term)和正则化项(regularization term).
而且,正则化项仅仅对应于一个去噪子问题!!!所以,这使得能够将任何的判别式降噪器集成到model-based 优化方法中。
--不采用学习一个MAP推导指导的判别模型,而是采取一个朴素的CNN去学习降噪器;
-- 已学习的CNN降噪器作为一个模块嵌入到model-based 优化方法中,去解决inverse 问题;
Image Restoration with Denoiser prior
--之前有借助ADMM变量分离技术的即插即用的先验架构;
--之前有提出使用HQS技术进行图像的降噪和去模糊的;
基于以上一些降噪先验的related work, 我们可以看出,降噪器先验可以通过多种方法插入迭代方案(iterative scheme);
迭代方案涉一个保真项相关子问题和一个降噪子问题;
Method:
--可以帮助噪声先验(denoiser prior),which作为基于模型的最优化方法的其中一个模块来解决这些逆问题(e.g., deblurring).
--噪声先验通过判别式学习方法(discriminative learning method)获得;
So, 结合上面两点,==》通过CNN训练一个噪声器,加入到基于模型的最优化方法来解决其他的逆问题;
在变量分离技术的帮助下,我们可以同时使用两种方法的各自优点;
变量分割技术(variable spitting techniques):
变量分离技术(variable splitting technique),如ADMM(alternating direction method of multipliers ),HQS(half quadratic splitting)方法,使得可以分别处理保真项(fidelity term)和正则项(regularization term),其中正则项仅对应于去噪的子问题。因此,可以在基于模型的优化方法中使用discriminative denoisers,本文的目标在于训练一系列快速高效的discriminative denoisers,并把它们用于基于模型优化的方法中,解决求逆问题。不使用MAP相关方法,而是使用CNN学习denoisers。
(也可以理解为基于模型的方法一般需要反复迭代去解这个公式,而基于判别学习的方法则通过损失函数去学习先验参数。这里可以将两者进行结合,正则项可以对应于一个去噪的子问题,这个子问题可以通过判别式学习的去噪器去获得,从而带来图像先验,使得基于模型的方法可以快速工作)
贡献:
-训练出一系列CNN denoisers。使用变量分离技术,强大的denoisers可以为基于模型的优化方法带来图像先验。
-学习到的CNN denoisers被作为一个模块部分插入基于模型的优化方法中,解决其他的求逆问题。
半二次方分裂 Half Quadratic Splitting (HQS)
$\hat{x}=\left. arg \text{ }min \right|_{x} \frac{1}{2}|| y-H x||^{2}+\lambda \Phi(x) \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(2)$
引入辅助变量$z, z = x$,HQS尝试最小化下面的成本函数:
$L_{\mu}(x,z)=\frac{1}{2}|| y-H x||^{2}+\lambda\Phi(z)+\frac{\mu}{2}||z-x||^{2}\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(5)$
$\mu$ 惩罚参数,在接下来的迭代求解过程中以非下降阶(non-descending order)的形式变化;
等式(5)可以被下面两个迭代的式子所解决:变量分割技术,
$x_{k+1}=\left. arg\text{ }min \right|_{x}|| y-H x||^{2}+\mu||x-z_k||^{2}\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(6a)$
$z_{k+1}=\left. arg\text{ } min \right|_{z}\frac{\mu}{2} ||z-x_{k+1}||+\lambda\Phi(z)\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(6b)$
可以看到保真项与正则化项被分开到两个子问题中
等式(6a)保真项在二次正则化最小二乘问题,有很多针对不同的退化矩阵的快速解法,最简单的解法是
$x_{k+1}=(H^{T}H+\mu I)^{-1}(H^{T}y+\mu z_{k}) \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(7)$
正则化项涉及在6(a)中,可以重写为(8)
$z_{k+1}=\left. arg\text{ } min \right|_{z} \frac{1}{2(\sqrt{\lambda / \mu})^2} ||x_{k+1}-z||^2+\Phi(z)\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(8)$
通过贝叶斯概率公式,等式(8)可以看做是对应于一个去噪任务,噪声水平为$\sqrt{\lambda / \mu}$,所以可以通过去噪器实现求出$z_{k+1}$.
以噪声水平$\sqrt{\lambda / \mu}$高斯去噪器的去噪图像$x_{k+1}$.去噪器可以作为(2)的模块,为了强调这个,重写(8)
$z_{k+1}=Denoiser(x_{k+1},\sqrt{\lambda / \mu})\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(9)$
值得注意的是图像先验$\Phi$可以间接被去噪先验替代,这种解法有一些优点:
-- 他允许使用各种灰度和彩色降噪器去解决各种inverse 问题;
-- 求解Eqn2时,显式图像先验$\Phi(\cdot)$是未知的;
-- 利用多个互补(complementary)的去噪器,利用不同的图像先验,可以共同解决一个特定的问题;
图像恢复的MAP推理公式:
$\hat{x}\text{}=\text{}$arg min$_{x}\frac{1}{2}||\textbf{y}\text{}-\text{}\textbf{H}x||^{2}\text{}+\text{}\lambda\Phi(x)$
正则化项$\Phi(x)$对应恢复的表现扮演了至关重要的角色:
$\textbf{z}_{k+1}\text{}=\text{}Denoiser(\textbf{x}_{k+1},\sqrt{\lambda/\mu})$
然后介绍现在的降噪先验只要采取model-based 优化方法去解决inverse problem,包括:
-- total variation(TV)法 ==》 常常制造watercolor-like 鬼影、伪影
-- 高斯混合模型(Gaussian mixture model,GMM)
-- K-SVD ==》高计算消耗
-- 非局部均值(Non-local means) ==》如果图像不具有自相似属性,会过度平滑不规则的结构
-- BM3D==》 如果图像不具有自相似属性,会过度平滑不规则的结构
图像的颜色先验是一个十分重要的考虑因素,因为图像大多数图像是RGB格式。
而由于不同图像通道之间的相关性,联合处理图像的不同通道常常会产生更好的表现比独立处理每个颜色通道。
许多工作都只对灰度图像进行建模,而对于彩色图像的建模较少;
作者指出CBM3D 因为联合处理了RGB通道,收获了不错的效果,同时作者提出可以使用判别学习方法去自动化的揭示潜在的彩色图像先验,而不是依靠手工设计的pipeline;
CNN降噪先验具有速度、表现、判别彩色图像建模的优势,同时CNN去学习判别式降噪器(discriminative denoiser)有一些原因:
-- CNN 的前向传播由于GPU的存在而并行计算
-- CNN 表现出了强大的先验建模能力with deep architecture
-- CNN利用外部先验,作为了BM3D为代表的内部先验的补充
-- 利用判别式学习的优势
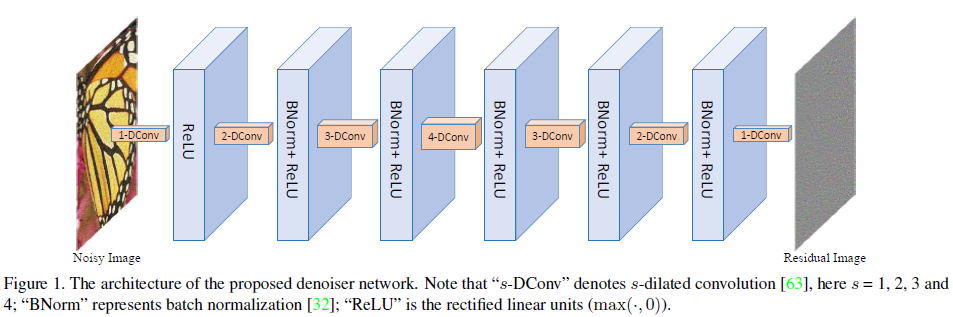
模型结构
CNN denoiser 如上图所示,网络包含七层,其中第一层是"扩张卷积(扩张指标为1,感知域还是3*3)+RELU",2-6层为“扩张卷积(扩张指标分别为2 3 4 3 2)+BN+RELU”, 最后一层为“扩展卷积(1),相当于正常的卷积运算,且每个中间层的特征图的数量都为64
扩张卷积filter and 增大的感知域
-- 在图像降噪中,上下文的信息能够促进毁坏像素的重建;
-- 为了捕获上下文的信息,通过前向的卷积操作去增大感知域是一个成功的方法;
有两种基本的增大感知域的方法:
-- 一个是增大filter size 弊端:会引入更多的参数,增大了计算负担
-- 一个是增大模型的深度
使用扩张卷积去获取filter size 和模型深度的平衡, 在保持 3*3 filter 的基础上 增大感知域, 整个7层网络实现了 33*33 的感知域, 相当于16层的3*3普通卷积;
其中扩张卷积的filter size 和 扩张指标s 之间的关系为: size = (2s+1)*(2s+1)
使用BN和残差学习加快训练
对于高斯降噪问题,结合BN和残差学习是十分有帮助的,他们都能够互相的获益(在他的论文中有讲Residual learning of deep CNN for image denoising.) 对于模型的迁移也有用;
残差学习方式,就是模型的目标不是直接学习产生降噪的图片,而是学习噪声即残差,即输入的带噪声的图片和干净图片的差。
使用小尺寸的图像作为训练集去避免边缘伪影
-- 由于CNN的特点,如果没有合适的处理,CNN的降噪图片将会产生边缘伪影;
-- 对称pandding 和 zero padding是两种解决这个问题的方法
-- 对于扩张指数为4的操作,在边缘pads 4 zeros,那其他的扩张指数呢?
-- 经验主义的使用了小尺寸的训练样本 去避免边缘伪影,原因包括:
-- 将大尺寸的图像crop 成小尺寸的patches,有利于CNN去看到更多的边沿信息,比如将70*70的patches crop成四个非重叠的35*35的patches,边缘信息被扩大了;
-- 就patch的大小可以作对比试验进行验证;
-- 当训练的patch尺寸小于感知域后,这个性能会下降;
学习实际的降噪器模型with 小间隔的噪声水平
-- 想要得到精确的子问题的解是非常困难且time-consuming的去优化的,使用不精确但是快速的子问题的解能够加快收敛(两篇文献:The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices.和 From learning models of natural im age patches to whole image restoration.)
-- 所以 没有必要去学习很多判别式降噪模型for 每个噪声水平。
-- 尽管$\textbf{z}_{k+1}\text{}=\text{}Denoiser(\textbf{x}_{k+1},\sqrt{\lambda/\mu})$ 是一个降噪器,但他与传统的高斯降噪有着不同的目标。
-- 传统的高斯降噪是恢复出潜在的干净图像,无论要去噪的图像的噪声类型和噪声水平如何,这里的去噪器都会发挥自己的作用。也就是说,不管这个图像有没有噪声,都会发挥作用!
-- 所以一个理想的判别降噪器应该使用当前的噪声水平进行训练:
训练了一系列的噪声水平在0-50同时独立的以2为间隔的模型,产生了25个模型为图像的先验进行建模;迭代方案的存在,使他恢复足以满足。
实验
图像降噪:
-- 将每个图片 crop 成了35*35的patches,因为使用残差学习的方式,损失函数:
$\textit{l}(\Theta)\text{}=\text{}\frac{1}{2N}\sum_{i=1}^{N}||f(y_{i};\Theta)\text{}-\text{}(y_{i}\text{}-\text{}x_{i})||^{2}$
-- 训练结束的标志 训练损失在五个连续的epoch固定
-- 使用了旋转翻转等数据扩充技巧;
-- 从不同方法的PSNR 进行了对比, 分别书灰度图和彩色图
-- 从不同方法的运行时间进行了对比
图像去模糊:
模糊核的选择:
-- 一个常见的模糊的高斯模糊核,标准差为1.6, 来自论文(Understanding and evaluating blind deconvolution algorithms)的前两个的真实模糊核;
-- 我们只需将颜色去噪器插入到HQS框架中;
-- 在公式6中:
![]()
-- 两个参数中,$\lambda$ 与$\sigma^{2}$相联系同时在迭代中保持固定,其中$\mu$控制着降噪器的噪声水平;
公式6(a)的快速解法:
$x_{k+1}=(H^{T}H+\mu I)^{-1}(H^{T}y+\mu z_{k}) \text{ }\text{ }\text{ }\text{ }\text{ }\text{ }(7)$
-- 由于hqs框架是基于去噪的,因此我们将每次迭代中去噪的噪声级隐式的确定为μ。
-- 在我们的实验设置中,根据噪声水平,它以指数形式从49衰减到[1,15]中的值。
-- 实验代码核心迭代部分
%模拟仿真的模糊噪声图片
k = fspecial('gaussian', 25, 1.6);%相当于是模糊算子
y = imfilter(im2double(x), k, 'circular', 'conv') + sigma*randn(size(x));
%denominator 表示是H^{T}H, H模糊算子与他的共轭矩阵相乘
V = psf2otf(k,[w,h]);%psf2otf(PSF) 其作用是将一个空间点扩散函数转换为频谱面的光学传递函数,执行的也是对PSF的FFT变换,变为了频域;
denominator = abs(V).^2;%y = abs(3+4i) y=5
%H^{T}*y H的共轭矩阵乘以输入y
upperleft = conj(V).*fft2(y); % conj(V) V=5-2i ==> 5+2i
%训练的特点噪声水平\sigma的一组denoiser,其\sigma以指数形式的衰减的不同模型;
modelSigmaS = logspace(log10(modelSigma1),log10(modelSigma2),totalIter);
%\lamba与噪声水平\sigma^2有关且在迭代中保持固定,\mu控制着降噪器的噪声水平,%rho隐式的表示\mu,见下面的计算方法与降噪器的噪声水平和噪声水平有关
rho = lamda*255^2/(modelSigmaS(itern)^2);%[243.742,267.099,292.694,320.742,351.476]
upperleft =
for itern = 1:totalIter
%%% step 1
rho = lamda*255^2/(modelSigmaS(itern)^2);
z = real(ifft2((upperleft + rho*fft2(z))./(denominator + rho)));
if ns(itern+1)~=ns(itern)
[net] = loadmodel(modelSigmaS(itern),CNNdenoiser);
net = vl_simplenn_tidy(net);
if useGPU
net = vl_simplenn_move(net, 'gpu');
end
end
%%% step 2
res = vl_simplenn(net, z,[],[],'conserveMemory',true,'mode','test');
residual = res(end).x;
z = z - residual;
end
真实模糊图像的测试
设置了两个重要的估计图像噪声水平 和 降噪器去噪水平的 超参数:
% There are two important parameters to tune:
% (1) image noise level of blurred image: Isigma and
% (2) noise level of the last denoiser: Msigma.
%使用了 别人的方法 产生的模糊核 图像作为先验的条件
%% read blurred image and its estimated kernel
% blurred image
Iname = 'im01_ker01';
y = im2single(imread(fullfile(folderTestCur,[Iname,'.png'])));
% estimated kernel
%k = imread(fullfile(folderTestCur,[Iname,'_kernel.png']));
k = imread(fullfile(folderTestCur,[Iname,'_out_kernel.png']));
if size(k,3)==3
k = rgb2gray(k);
end
k = im2single(k);
k = k./(sum(k(:))); %归一化
%比较重要的部分是边缘的处理
%% handle boundary
boundary_handle = 'case2';
switch boundary_handle
case {'case1'} % option (1), edgetaper to better handle circular boundary conditions, (matlab2015b)
% k(k==0) = 1e-10; % uncomment this for matlab 2016--2018?
ks = floor((size(k) - 1)/2);
y = padarray(y, ks, 'replicate', 'both');
for a=1:4
y = edgetaper(y, k);
end
case {'case2'} % option (2)
H = size(y,1); W = size(y,2);
y = wrap_boundary_liu(y, opt_fft_size([H W]+size(k)-1));
end
需要明白为什么需要进行边缘条件的变化,是让模糊核完全重合和图像,所以需要用模糊核 进行 一些 padding 操作
降噪的代码,论文并没有提供在实际环境中应用的代码;
% clear; clc;
addpath('utilities');
imageSets = {'CBSD68','Val20'}; %%% testing dataset
folderTest = 'testsets';
folderModel = 'models';
folderResult = 'results';
taskTestCur = 'Denoising';
if ~exist(folderResult,'file')
mkdir(folderResult);
end
setTestCur = imageSets{1};
imageSigmaS = [5,10,15,25,35,50];
modelSigmaS = [5,10,15,25,35,50];
showResult = 1;
saveResult = 0;
useGPU = 1;
pauseTime = 1;
%%% folder to store results
folderResultCur = fullfile(folderResult, [taskTestCur,'_',setTestCur]);
if ~exist(folderResultCur,'file')
mkdir(folderResultCur);
end
%%% read images
ext = {'*.jpg','*.png','*.bmp'};
filePaths = [];
folderTestCur = fullfile(folderTest,setTestCur);
for i = 1 : length(ext)
filePaths = cat(1,filePaths, dir(fullfile(folderTestCur,ext{i})));
end
%%% PSNR and SSIM
PSNRs = zeros(length(modelSigmaS),length(filePaths));
SSIMs = zeros(length(modelSigmaS),length(filePaths));
load(fullfile(folderModel,'modelcolor.mat'));
for i = 1:length(modelSigmaS)
disp([i,length(modelSigmaS)]);
net = loadmodel(modelSigmaS(i),CNNdenoiser);
net = vl_simplenn_tidy(net);
% for i = 1:size(net.layers,2)
% net.layers{i}.precious = 1;
% end
%%% move to gpu
if useGPU
net = vl_simplenn_move(net, 'gpu');
end
for j = 1:length(filePaths)
%%% read images
label = imread(fullfile(folderTestCur,filePaths(j).name));
[~,imageName,extCur] = fileparts(filePaths(j).name);
label = im2double(label);
randn('seed',0);
input = single(label + imageSigmaS(i)/255*randn(size(label)));
%%% convert to GPU
if useGPU
input = gpuArray(input);
end
res = vl_simplenn(net,input,[],[],'conserveMemory',true,'mode','test');
output = input - res(end).x;
%%% convert to CPU
if useGPU
output = gather(output);
input = gather(input);
end
%%% calculate PSNR and SSIM
[PSNRCur, SSIMCur] = Cal_PSNRSSIM(im2uint8(label),im2uint8(output),0,0);
if showResult
imshow(cat(2,im2uint8(label),im2uint8(input),im2uint8(output)));
title([filePaths(j).name,' ',num2str(PSNRCur,'%2.2f'),'dB',' ',num2str(SSIMCur,'%2.4f')])
drawnow;
if saveResult
imwrite(im2uint8(output),fullfile(folderResultCur,[imageName,'_',num2str(imageSigmaS(i)),'_',num2str(modelSigmaS(i)),'_',num2str(PSNRCur,'%2.2f'),'.png']));
end
pause(pauseTime)
end
PSNRs(i,j) = PSNRCur;
SSIMs(i,j) = SSIMCur;
end
end
%%% save PSNR and SSIM metrics
save(fullfile(folderResultCur,['PSNR_',taskTestCur,'_',setTestCur,'.mat']),'PSNRs')
save(fullfile(folderResultCur,['SSIM_',taskTestCur,'_',setTestCur,'.mat']),'SSIMs')
disp([mean(PSNRs,2),mean(SSIMs,2)]);




 浙公网安备 33010602011771号
浙公网安备 33010602011771号