拟合和过拟合

 

$(x^{i},y^{i})$   example

$h_{\theta}(x^{i})=$

 

损失函数

$J(\theta) = 1/2SUM(h(x_{\theta}^{i}))$

 

欠拟合和过拟合

一个线性模型 拟合房价曲线

$\theta_{0}+\theta_{1}x_{1}+......$ 多个项进行拟合

对房价曲线进行拟合 

线性拟合  欠拟合 underfitting  $\theta_{0} + \thata_{1}x_{1}$  

二次拟合 

多次项的拟合   过拟合  overfitting

 

 

参数学习算法参数学习算法是一类有固定数目，参数的用来进行数据拟合的算法，线性回归即是此类

 

非参数学习算法则是一类参数数目随数据集增大而变多（一般是线性增大）的算法：

局部加权算法(LOESS)

局部加权回归算法是对线性回归的扩展，当目标假设是线性模型时，使用线性回归自然能拟合的很

 

当我们在预测一个点的值时，我们选择和这个点相近的点而不是全部的点做线性回归。基于这个思

想，就有了局部加权回归算法

 

 

 

 

 

，w(i其中)是权值，它的作用在于根据要预测的点与数据集中的点的距离来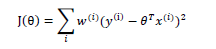

为数据集中的点赋权值，当某点距离待预测点较远时，其权重较小，否则较大。
一个较好的函数如下：

 

离得远的点贡献比较小 离得近的点贡献比较大  注意这和高斯分布没有关系

 

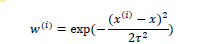
该函数被称为指数衰减函数。其中，\tao被称为波长参数，它控制了权值随距离下降的速度

 

局部加权回归  非参数学习算法  我们不考虑是否建模 

怎么确定波长参数？尤其的重要.

 如果数据集特别大 非参数算法 的复杂度非常高

 

线性回归的概率解释

 

 

接下来对线性回归的最小二乘法的合理性做了概率解释，即为什么选择平方函数作为目标函数会使得效果比较好？

 

假设1

误差项可以看作是随机噪声 忘了建模的参数

 

我假设误差项 服从 高斯分布 均值为0

那么假设二为何会成立呢？这是因
为影响误差的因素有很多，这些因素都是随机分布，根据中心极限定理（Central
Limit Thoery），即许多独立随机变量的和趋向于正态分布，我们可以得到假设二

 

误差为什么服从高斯分布  根据中心极限定理  通常是服从高斯分布  

误差由许多效应组成

 

 概率密度函数

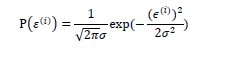
加入参数项

这也表示，当给定参数𝜃和x 时，目标值y 也服从正态分布：

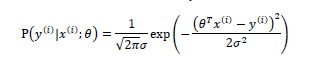
\theta 有确定的值 以\theta为参数的....服从高斯分布

(..)

差

iid
，independent and
：对于各个样例的误
，它们
（独立同分布，i
identical distribution）
随机变量

 

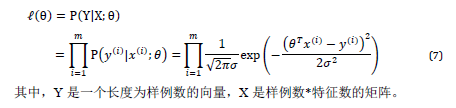
一系列高斯密度函数的乘积 \theta的似然性 和 概率性 试图强调 X是固定的

参数的似然性和数据的概率 而不是反的

idd 怎么去估算参数？？

 

极大似然估计 选择参数\theta  使得数据出现的可能性尽可能大

 所以要选择 \THETA 使似然性最大化 

选择参数 使得数据的出现尽可能大  出现的概率最大化 

$L(\THETA) = logL(\THETA)$  对数似然函数 对L（\THETA）取对数的结果

 

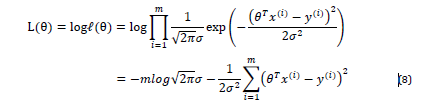
 所以对L 取最大化 ， 可以说是对这一项去最小项

 

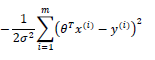
这一项就是 之前我们使用的成本函数   注意这里的假设的是 误差项服从高斯分布且独立同分布

使得似然性最大化 

 

第一个分类算法

 

洛吉斯特回归

假设我们的值总是在 零和一之间 

不会用线性函数进行描述

选择 函数

sigmoid 函数  

 概率解释 假设会产生 0和1 尝试出y=0 1 

组合得到 产生0 或者 1 的概率函数

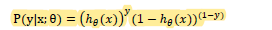
所以我们解决参数拟合问题

怎么拟合出参数 

 

参数似然性 

 

省略下标  \theta

找到参数的极大似然估计 

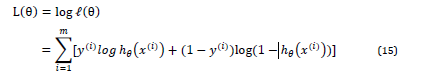
为了拟合出模型中的参数\theta 

同样使用学习过的梯度下降法 使用相同的算法 最大似然

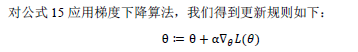
对数似然性与\theta有关 

梯度上升法

导出梯度下降的方法 对\theta 求偏导

梯度上升的规则 如上所示  当我在最小二乘公式中 这里的负号被修改了 但是是一个相同的学习算法  

所以分类问题 并不糟糕

原始是 洛吉斯特回归和上一次的回归是一个线性函数 他们看上去相似  并不是巧合

模型 学习过程中 进行了求导。