(CS229)监督学习应用和梯度下降

监督学习：基于标记数据的学习

监督学习又举了两个例子：回归问题regression在连续数据上的模型构建问题  和 分类问题 classification 在离散数据上的问题

无监督学习：未标记的学习 经典方法是聚类cluster

 应用：使用聚类算法对图像进行处理，聚类处理，使图像更为明显像素分组；

            使用聚类算法将图像分成不同的部分 计算机集群组织 消费人群的划分 星系的组成

            鸡尾酒会问题： 多人说话的情况下 那个人的声音从声音中分离出来 可使用无监督学习的方法

 

强化学习： 利用监督学习进行预测； 通过评价函数，决定作出的决策是否是正确的，通常做出一系列的决策； 飞行控制器使用的就是强化学习
如何定义一个好的行为和一个坏的学习 通过学习性算法进行控制。

 

 

定义：

$m$为训练数据大小

$x$为输入变量，是向量

$y$为输出变量，是实数

$(x,y)$为一个训练实例

$(x^{i},y^{i})$是第i个训练实例，i是上标；

为了方便说明，又添加了一个变量，问题变为房屋面积和卧室数目(可以理解为向量由两个参数组成)与房屋价格的关系

 

训练集中的数据使用线性回归问题进行解决：

$h(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}=\sum_{i=0}^{2}\theta_{i}x_{i}=h_{\theta}(x)$

其中，$h_{\theta}(x)$ 表示以$\theta$为参数的。公式如下：

$h_{\theta}(x)=\sum_{i=0}^{n}\theta_{i}x_{i}=\theta^{T}x$  ==》单个样本的前向推导，也看看作是矩阵的相乘，x由多个变量组成，相应的定义多个参数$\theta$进行线性相乘再累加，相当于进行加权求和，得到输入向量对应于的输出变量的表征，不同的特征具有不同的权重$\theta$。

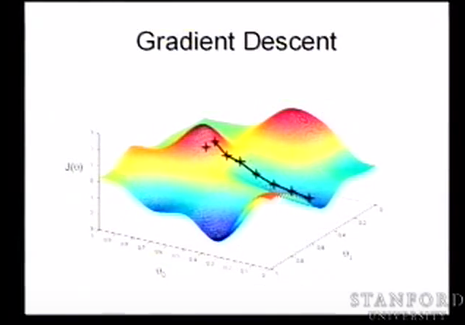
x是向量，n是x的长度，从而定义目标函数

$J(\theta)=1/2\sum_{i=0}^{m}(h_{\theta}(x^(i))-y^{i})^2$ ==》对整个数据集m 进行优化，使用了平方损失，前面加上一个1/2方便BP时反向的求导，加快计算。