(Review cs231n) BN and Activation Function

CNN网络的迁移学习(transfer learning)

1.在ImageNet上进行网络的预训练

2.将最上方的层，即分类器移除，然后将整个神经网络看成是固定特征提取器来训练，将这个特征提取器置于你的数据集上方，然后替换原先作为分类器的层，根据数据集的大小来确定如何对卷积网络的最后一层进行训练，或者你可以对整个网络的一部分反向传播进行微调。

3.如果你有更大的数据集，你可以在整个网络进行更深的反向传播

拥有大量的预训练好的模型，所以没有大量的数据也不会有太多影响，你只需要找一个经过预训练的卷积神经网路然后进行finetune

训练的时间有限和资源有限

 神经网络的发展训练过程

1.感知机模型

2.多层感知机模型

3.反向传播的概念被提出研究了多层次感知机，提出了损失函数，梯度下降

4.hiton第一次建立了神经网路模型，合理训练10层神经网路，采用了无监督与训练的方案，使用了

RBM(限制波尔茨曼机)，不是在单通道中对所有层都经过反向传播，一层无监督，不断堆叠，进行整合。然后进行反向传播和微调。总体思路：逐层预训练，然后整合起来进行反向传播。

激活函数

1.sigmoid

 

                                            

缺点：

1.神经元过于饱和，输出要么非常接近0，要么非常接近1，这些神经元会导致在反向传播算法中出现梯度趋0的问题，这个问题叫做梯度消失

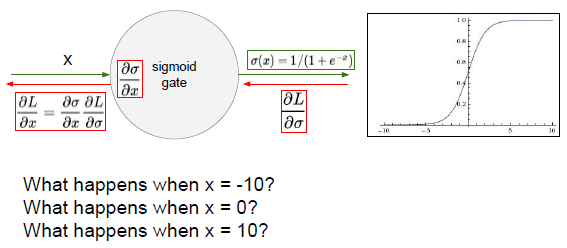
当X取-10和10的时候。梯度会非常的小。对于局部梯度dsigma/dx可以看到在取值-10的地方，他的梯度几乎为0，因为这里的斜率是0。

一旦值达到饱和，梯度也趋于0，当乘以很小的数时，sigmoid的梯度传播将会停止。梯度很快停止，数据停止更新

2. sigmoid函数的输出不是关于原点中心对称的，不关于原点中心对称的输出值都集中在0和1之间，非中心对称的输出总是不对。

当输入sigmoid的值x都为正数时，权重w怎么变化？ 梯度从上层传播下来，w的梯度都是用x乘以f的梯度，如果神经元输出的梯度都是正的，w的梯度就会是正的。所以W的梯度要么为正，要么为负。因此他的问题据说被这种条件约束了。根据经验得出，如果训练的数据并不关于原点中心对称，那么收敛速度会非常的慢，必须搞清楚fisher矩阵和神经梯度，希望得到关于原点中心对称的输入和中心对称的输出，收敛会更好。

3.x的计算相对耗时多，exp

2. Tanh(x)

输出-1和1，关于原点对称，值仍然容易饱和，导致梯度消失，tanh优于sigmoi,

3.Relu

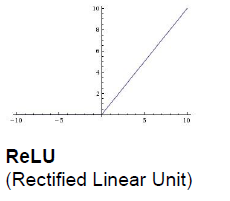
优点：

1.首先不会饱和，至少为正的时候不会，在正的区域不会发生梯度的消失，梯度不会突然为0，当神经元只在很小的时候，在边界区域被激活时，才会出现这种问题，但实际上这些神经元只是在反向传播过程中被激活，在一半的区域内，反向传播不会变为0，

2.计算非常的高效

3.收敛非常的快。

缺点；

1.不关于原点中心对称。

2.在反向传播时，当输入的神经元小于0，

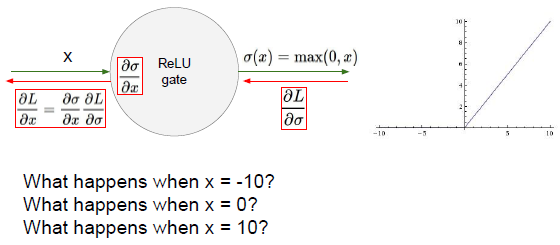
当取值-10那么局部梯度为0，因为这部分斜率为0，这不仅仅是缩小了梯度，将梯度变为0，权重不会更新

当取值10那么局部梯度为1，Relu直接将这一梯度传给前面，直接传播梯度，否则直接杀掉梯度。

当取值为0.这一点梯度不存在，条件是它的原函数必须是可微的

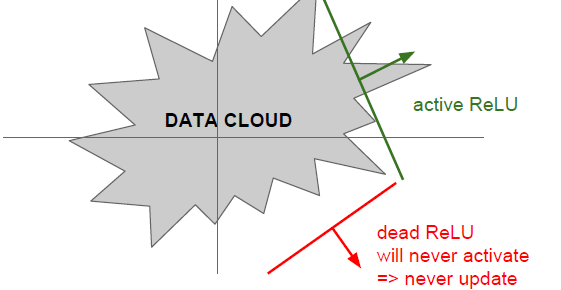
如果神经元在数据集外面，那么dead Relu将会永远不会被激活，参数也不会更新：一种是在初始化阶段，你非常不幸的把权重设置成不能使神经元激活的数值，这种情况神经元不会训练；更多的情况下是训练过程中你的学习率太高了，想象一下神经元在一定范围内波动，可能会发生数据多样性丢失，这种情况下神经元不再被激活，数据多样性丢失不可逆转，

当你训练一个大的，激活函数为Relu神经网络，你可能会发现有10%-20%的神经元死掉，这些神经元不再会被训练集中任何数据激活，通常情况下学习率太高了造成的。

在初始化过程中，因为Relu的dead problem, 人们把偏置值设置成很小的正数比如0.01，而不是设置成0，这有可能使未经初始化的Relu更有可能输出正值，从而参数得到更新，

4. Leaky Relu 

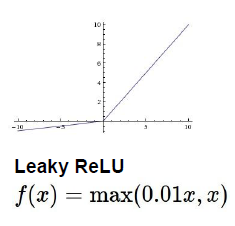
解决负向空间中梯度消失的问题，在这个区间给出了很小的负或正的斜率而不是0，解决dead problem

5. ELU

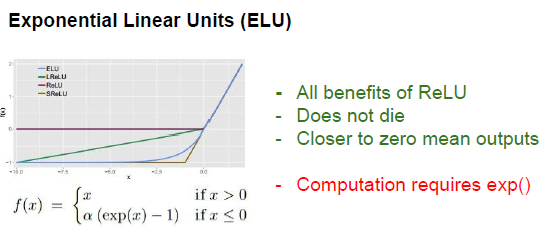
继承Relu的优点，并且不会输出不是0中心的问题，这样可以得到0均值的输出。

 

不同的激活函数是你得到最后不同的权重值，反向计算的动态过程会不一样，所以你得到不同的权值。

实际优化的建议：

数据预处理

 

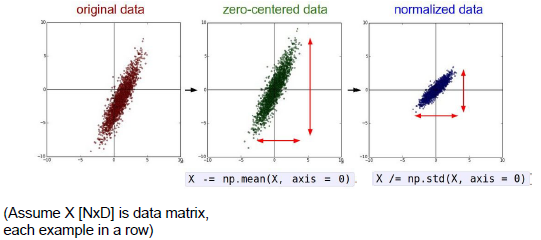
数据预处理是假设你有一个二维原始数据团，并且数据团以（2，0）为中心，意味着我们要让每一个特征值减去均值，在每个维度上通过除以标准差进行标准化（数据归一化），或者确保每个维度最大值和最小值在-1和1之间等方法。对于图像所有特征都是像素，并且取值在0到255之间，但是图像处理中归一化并不常见，但是零中心化应用很多。

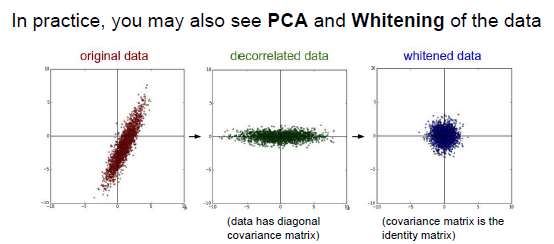
数据存在协方差，可以应用PCA算法将协方差矩阵变为对角矩阵，并将数据进行白化。

经过PCA对数据进行压缩后，使协方差矩阵变为单位矩阵（通常在图像中不这么做，因为协方差矩阵会非常的大）

在图像处理中常见的是均值中心化处理，例子：

1.最后得到一个32*32*3的均值图像，ImageNet每张图像减去均值图像以进行中心化处理从而训练效果

2.减去单通道均值，在红绿蓝三色通道中分别计算，最后得到三个数值

权重初始化

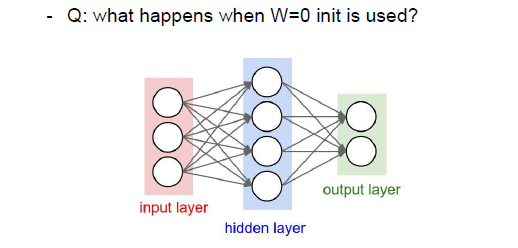
所有的神经元都是一样的，在反向传播中它们的运算方式也是一样的，完全对称，相同的计算，相同的梯度，所以用很小的随机数进行代替。

从标准差为0.01的高斯式中随机抽取，但是层数增加，会存在问题，当取样1000个500维的数据，创建一整个隐含层和非线性映射函数，我们有10层网络，每层包含500个单元，我们使用Tanh函数。

使用高斯分布来初始化权重乘以权值0.01，然后进行网络的传播，在传播过程中关注权重的均值和标准差。

 

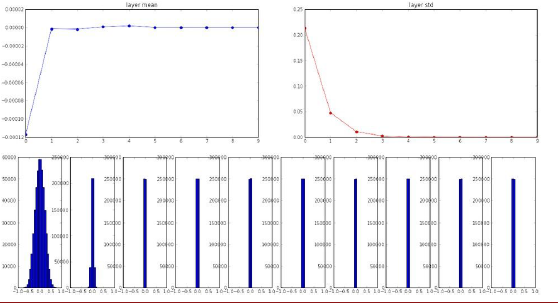
所有的均值会归于0，方差一开始是1，接下来的层它会变成0.2.....直线下降到0。

第一张图比较合理，数据处于-1和1之间，之后数据开始塌缩，只分布在0上，最终所有Tanh为激活函数的神经元都输出0。

首先看看这层之前的那些层，它们给这层输入的都是小量数值，那些层上W的梯度会是怎样？w的梯度等于x乘以上一层的梯度，x是小量，W的梯度也是小量，这些值对于梯度的叠加几乎没影响。

当我们在该层中进行链式求导，前向传播时，我们关注W的梯度，都是微小量；反向传播时我们要求x的梯度，于是反向传播的过程中，我们在每一层，不断的乘以W。

数据单高斯分布，并不断乘以W，最终值趋于0，在反向传播过程中，会出现这样的情况，我们不断的乘以W，我们从合理的损失函数开始，在进行反向传播时，不断趋于0，所以整个网络的梯度相当小，这就是梯度消失，梯度的量级不断减小。

我们将权值从0.01变为1.0

 

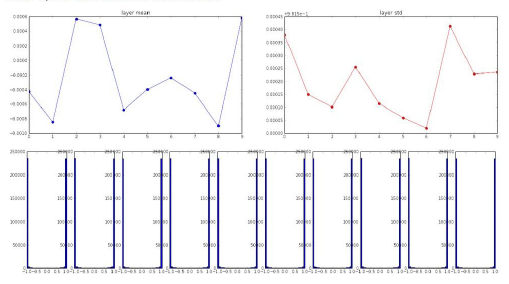
所有的数值都趋于饱和，-1 or 1，因为权值设置太高了，Tanh神经元的输出都饱和了，梯度接近0，网络停止工作。

Xavier 初始化：

使梯度的大小合适，每个神经元的输入开根号，如果很多的输入，将会有有较小的权值，因为加权和中被算入的量增多了，并且希望它们之间的相关性降低；

Tanh函数是非线性的，将数据的方差改变，标准差减小。

 

但是它在Relu中并不奏效，方差下降的会更快，越来越多的神经元没有被激活。Relu神经元让方差减半，我们在Xavier初始化基础上添加了系数2，得到了Relu的合理分布，如果没有2，激活输出的分布会以指数级收缩。

 

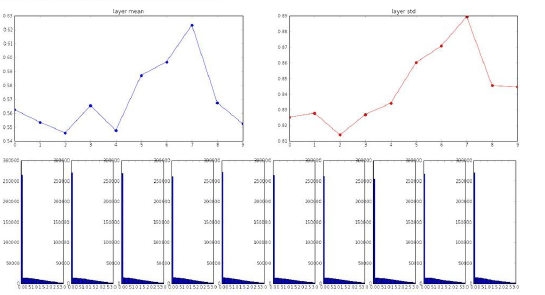
Batch Normalization 数据规范化

你想神经网络中每一部分都有粗略的单位高斯激活，如果想让某个东西单位高斯，就等同于这个可微分方程，

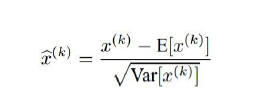
你可以尝试对它运行BP算法，你会发现你选了你数据的一个小分批，对整个神经网络执行它，接下来我们把执行批量数据正则化(batch normalization layer)的层插入到你的神经网路，这些层接收你的输入X。

这些层保证了你这批数据的每一个特征维度都有单位高斯激活(unit gaussian activation)。

Batch Normalization的步骤：

1.设批数据里有N个东西，并有D个特征(activation of neurons)，在神经网络的某个位置，就是批数据规范层(batch normalization layer)的输入，这是一个有X个激活的矩阵，批量数据规范化高效的计算出了每一个特征(feature)的经验均值(empirical mean)和方差(variance)，然后执行这个方程，所有不管X是什么，batch normalization 保证这里的每一列的每一个单位都是unit Gaussian，所以这是一个完美的可微分的方程，对于批数据里的每一个特征或是激活都执行。

引入batch normalization layer层的位置：

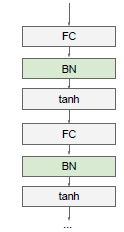
BN层保证了神经网络的每一步的每一个东西都是roughly unit Gaussian的。

这个不必要的约束，确保Tanh层的输入是unit Gaussian的，因为你想要你的网路自己选择是想要Tanh的输出是离散diffuse)一点的还是饱和（saturated）一点的，现在的网络结构实现不了以上功能，所以引入了BN层。

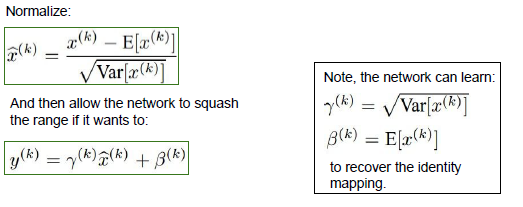
不仅仅局限于对X进行规范化，它还可以对X进行移动，通过用X乘以gamma再加上Bata，对于每一个输入的特征。

神经网络的功能变强大了，参数两个为我们需要备份的，它们使神经网络可以在得到unit Gaussian值后依然可以改变数值，我们把初始值设置成1和0，再调整这两个值。当设置了两个参数时，我们的神经网络可以从备份的信号值里选择，什么作为输入到Tanh层，通过调节输入可以做到调节Tanh的形状到你想要的结果为止，不会再遇到类似的一开始优化就遇到梯度消失或爆炸的问题。

当两个参数取为了上图右边的两个值时候，这个部分可以通过学习抵消BN的作用，所以BN其实等价于一个恒等函数，或者说可以通过学习达到恒等的作用。

BN算法：

引入BN层的优点：

1.增强了整个神经网络的梯度流

2.支持更高的学习速率，可以更快的训练模型

3.减小了算法对合理的初始化的依赖性，当改变初始值域的大小时，没有BN层会产生很大的区别，当采用BN层你会发现算法适用于更多的初始值。

4.BN层实际上起到了一些正则化的作用。=====》 当你使用X作为神经网络的输入时，在某一层的表达式却不仅仅包含X，他还包含了这一批数据里的其他例子，这批数据里的其他例子是与独立同时X并发执行的，所以BN层实际上把这些例子捆绑在一起了，每一层BN都是你输入的所以批数据的方程，有不错的正则化效果。

[3,5,7,2]======>经过BN层的结果 [-0.35,0.21,0.77,-0.63]

在测试时希望方程不变确定，在测试时BN层的作用并不相同，你使用两个参数进行规范化，在测试时你可以记住你全部数据的两个参数可以像对于每一个点计算mean和sigmoid一样计算出来，基于整个训练集一次性计算出来，确保BN可以记住这些值。

网络结构的选择

(1)、两个初始的检查：

1. 根据分类的类别数，如10类，则通过Softmax层后的初始损失应该是-log(1/10)=2.302585092994046,由此进行检查。

2.加入正则化后预期我们的损失值上升，因此加入了一个新的项。

(2)、使用数据集的一小部分尝试对于这部分数据你的模型可以过拟合：

1.基本上损失可以降为0，对于这部分过拟合的数据得到了100%的准确度，证明反向传播应该是在正常的工作，跟新也在正常的工作。

(3)、达到过饱和时，扩大数据量，找到合适的学习率，做一个grid search。

 刚开始训练时，损失会有小波动，但训练到最后，你的损失值还是很大，损失值变小的很慢，需要提高学习率。

超参数的优化

设置循环，在每一个循环对正则化系数和学习率进行采样，然后进行训练得到结果，在验证数据中得到结果。

确保超参数的性能好，最好对学习率和正则化率在对数空间中采样，因为学习率是一个乘法交互，

 

再根据已经随机取样的超参数进行进一步的缩小范围，这些学习率和正则化参数值都是在一个区间内随机取样，

 

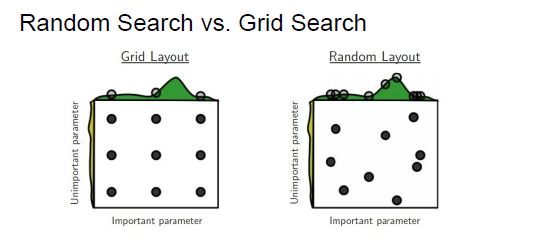
grid search 的性能没有随机取值好，用一个确定的区间来取值，并不确定是否得到了整个区域里最好的值，

往往存在一个超参数的重要性远远高于另一个，会发现在一个范围内的取值对损失的结果明显比在范围外得到的结果要好很多。

权重的初始化不好造成损失的变化奇怪：

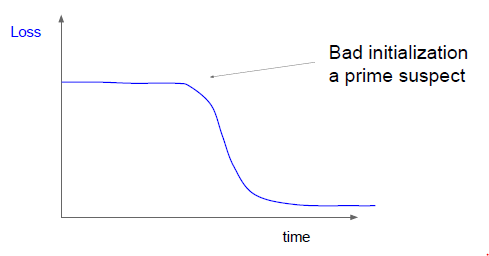
同时，我们也更关注分类的准确率，出现过拟合，尝试提高正则化参数；

这一部分略显模糊，关注参数大小以及参数更新量之间的区别，有一组权值，在反向传播过程中，权值会发生相应的变动或增量。这个增量相对于你的权值来说就不能太大，增量为1e-7，权值为1e-2，然后再观察一下权值的增量，在这里就是这个范数(norm)==》updata_scale，与这个权值param_scale作比较，值为1e-3最好。