(Review cs231n) The Gradient Calculation of Neural Network
前言:牵扯到较多的数学问题
原始的评分函数:

两层神经网络,经过一个激活函数:

如图所示,中间隐藏层的个数的各数为超参数:
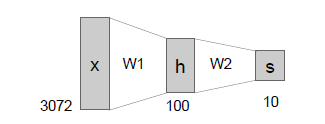
和SVM,一个单独的线性分类器需要处理不同朝向的汽车,但是它并不能处理不同颜色的汽车,它并不是一个好的分类器。
但是如果使用有一百个数值的中间层的神经网络,我们可以给这一百个数值赋值。
例如第一个数值处理朝向正前方的汽车;只用来识别朝向正前方的汽车,下一个数值用来处理朝向偏右的车等,得到的数值只有图片满足这些详细要求的时候才会正,其他情况下为0,接下来还可以处理不同颜色不同朝向的汽车,一个针对所有不同情况下汽车的模板,中间层会对所有的汽车进行表示,如果图像符合要求,就会得到正值 。
W2会对所有不同情况下的汽车模板进行汇总,比如我们现在有20种汽车模型,为了得到汽车分类器的评分,需要再加入一个矩阵乘法,用来给不同的汽车模型得到权重的合,如果一个汽车满足了一个模型,那么这个模型的输出再乘以一个正权重加入总评分。
100是隐藏层的大小,可以改变大小的超参数,自行选择适合的模型来匹配不同汽车的朝向问题。
一般超参数会选尽可能大的,取决于你的电脑是否支持。
一个三层的神经网络,想要扩展它,简单的添加重复的隐藏层。

把相同的隐藏层添加进去让网络更深。

矩阵求导的计算方式也是一样的,需要注意的一个细节是如果,计算
需要对
进行转置,计算
需要对
进行转置,并且因为
与
维度相同,
与
维度相同,所以我们在计算导数的时候关注一下矩阵维度,这样可以减少错误的概率。
两层神经网络的训练过程,使用三维矩阵来训练做二元分类的神经网络,y的标签是二进制数,使用逻辑回归损失:
"""
Created on Sat Mar 16 16:54:51 2019
@author: ckc
"""
import numpy as np
X = np.array([[0,0,1],[0,1,1],[1,0,1],[1,1,1]]) # size = 4*3 y = np.array([[0,1,1,0]]).T #size= 4*1, T 转置 weight1 = 2* np.random.random((3,4)) - 1 weight2 = 2*np.random.random((4,1)) - 1 #for j in xrange(60000): l1 = 1/(1+np.exp(-(np.dot(X,weight1)))) l2 = 1/(1+np.exp(-(np.dot(l1,weight2)))) l2_delta = (y - l2) * (l2*(1-l2)) # 第二层的梯度,dL/dz * dz/dx局部梯度,(y-l2为逻辑回归损失) l1_delta = l2_delta.dot(weight2.T) * (l1*(1-l1)) # 4*1 * 1*4 = 4*4 ,第一层的梯度 weight2 += l1.T.dot(l2_delta) weight1 += X.T.dot(l1_delta)
分析:

1. 每一层的delta为反向传播的chain rule 推导的结果,并为传播到q_{n}=w.dot(x)前,注意w需要进行转置为w^{T}以匹配维度。
2. 进行参数更新,W_{n} += dw_{n} , 其中dw_{n} = delta_{n}*(dq_{n}/dw_{})

其中:
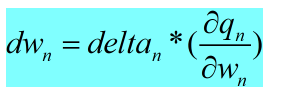
所以:

x的转置,用于匹配维度
每一个小的神经元都可以看作是一个小的线性分类器,这些神经元彼此相连,一起工作。
默认的非线性激活函数的选择Relu。
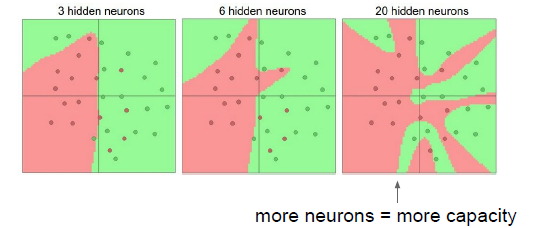
如图所示神经元的个数越多,分类性能越好,函数越复杂。
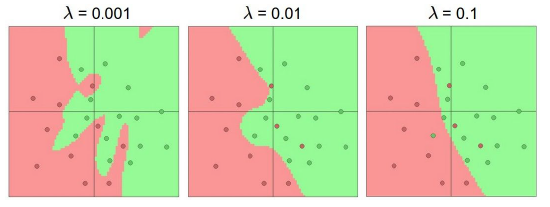
对模型添加正则化,正则化的表现是对高维度W的惩罚力度,当正则化系数很大,使得W变得非常小,最终的结果是函数变得非常的平滑,函数实际使用的变量减小,减小W系数,边界的扭曲程度变得很高,拟合程度更高,起作用的变量数量更多。
最少需要三个神经元,一个、两个、三个平面,也就是三个使用非线性函数作为激活函数的线性分类器,在分类平面中,你可以用三条直线来圈出一个空间,第二层只是把三条线合并在一起,最终得出结果0或1。
1.模型中网络越复杂,模型的表达能力越强,要使用引入正则化的方法,防止神经网络过拟合。
2.一般图像问题深度很重要,但是对于简单的数据,网络的深度没有多大的作用。
3.只选择一种激活函数,经常使用Relu。




